問題
次の文章は,平行板コンデンサに関する記述である。
図のように,同じ寸法の直方体で誘電率の異なる二つの誘電体(比誘電率 \(ε_{r1}\) の誘電体 1 と比誘電率 \(ε_{r2}\) の誘電体 2 )が平行板コンデンサに充填されている。極板間は一定の電圧 \(V\) [V] に保たれ,極板 A と極板 B にはそれぞれ \(+Q\) [C] と \(−Q\) [C] ( \(Q>0\) ) の電荷が蓄えられている。誘電体 1 と誘電体 2 は平面で接しており,その境界面は極板に対して垂直である。ただし,端効果は無視できるものとする。
この平行板コンデンサにおいて,極板 A , B に平行な誘電体 1 ,誘電体 2 の断面をそれぞれ面 \(S_1\) ,面 \(S_2\) (面 \(S_1\) と面 \(S_2\) の断面積は等しい)とすると,面 \(S_1\) を貫く電気力線の総数(任意の点の電気力線の密度は,その点での電界の大きさを表す)は,面 \(S_2\) を貫く電気力線の総数の \( \fbox { (ア) } \) 倍である。面 \(S_1\) を貫く電束の総数は面 \(S_2\) を貫く電束の総数の \( \fbox { (イ) } \) 倍であり,面 \(S_1\) と面 \(S_2\) を貫く電束の数の総和は \( \fbox { (ウ) } \) である。
上記の記述中の空白箇所(ア)~(ウ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
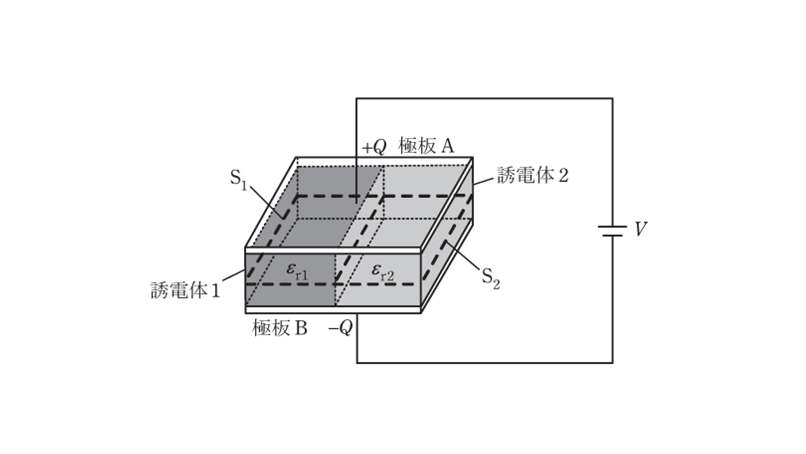
$$ \begin{array}{ccccc} \ &(ア)&(イ)&(ウ)\\ \hline (1) &1 &\displaystyle \frac{\varepsilon_{r1}}{\varepsilon_{r2}} &Q \\ \hline (2) &1 &\displaystyle \frac{\varepsilon_{r1}}{\varepsilon_{r2}} &\displaystyle \frac{Q}{\varepsilon_{r1}}+\displaystyle \frac{Q}{\varepsilon_{r2}} \\ \hline (3) &1 &\displaystyle \frac{\varepsilon_{r2}}{\varepsilon_{r1}} &\displaystyle \frac{Q}{\varepsilon_{r1}}+\displaystyle \frac{Q}{\varepsilon_{r2}} \\ \hline (4) &\displaystyle \frac{\varepsilon_{r2}}{\varepsilon_{r1}} &1 &\displaystyle \frac{Q}{\varepsilon_{r1}}+\displaystyle \frac{Q}{\varepsilon_{r2}} \\ \hline (5) &\displaystyle \frac{\varepsilon_{r2}}{\varepsilon_{r1}} &1 &Q \\ \hline \end{array} $$
解説
答え:(1)
(ア)面\(S_1\)を貫く電気力線の総数と面\(S_2\)を貫く電気力線の総数の比
今回の問の平行板コンデンサは内部の誘電体が左右で異なるので、2つのコンデンサが並列に接続されていると考えます。
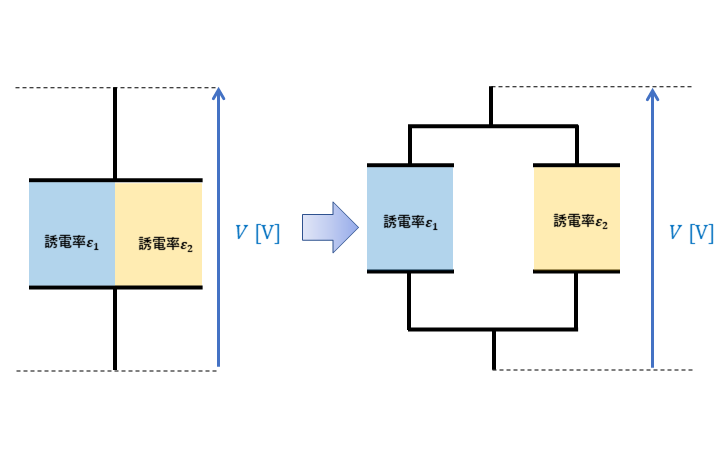
並列接続されている左右の平行板コンデンサそれぞれに加わる電圧は等しくなります。
ポイント①より、平行板コンデンサ内の電界の大きさは、
$$ E = V \times d $$
電圧\(V \ [V]\)と極板間の距離\(d\ [m]\)が同じ値となるため面\(S_1\)と面\(S_2\)の電界の大きさ\(E_{S1}\)と\(E_{S2}\)は同じ値となります。
また、問題文より面\(S_1\)と面\(S_2\)の大きさも等しいことが分かります。よって、面\(S_1\)と面\(S_2\)の電気力線の総数\(N_{S1}\)と\(N_{S2}\)は同じ値となります。
$$ \begin{align} N_{S1} = \frac{E_{S1}}{S_1} &= \frac{E_{S2}}{S_2}\\ &= N_{S2} \end{align}$$
よって、(ア)面\(S_1\)を貫く電気力線の総数と面\(S_2\)を貫く電気力線の総数の比は1となります。
電気力線の本数\( \displaystyle \frac{Q}{ε} \)を用いた考え方
面\(S_1\)側の極板に蓄えられる電荷を\(Q_{S1}\)、面\(S_2\)側の極板に蓄えられる電荷を\(Q_{S2}\)とおく。ただし、\(Q_{S1} + Q_{S2} = Q\)とする。
コンデンサの左右で内部の誘電率が異なる場合、2つのコンデンサが並列接続されているとみなすことができるので、左右の極板間に加わる電圧は等しくV[V]となります。
また、左右のコンデンサの静電容量を\(C_{S1}\)、\(C_{S2}\)と表すと\(C = ε \frac{S}{d}\)より
$$ C_{S1} = ε_{r1} \frac{S_1}{d} $$
$$ C_{S2} = ε_{r2} \frac{S_2}{d} $$
と書き表せます。
よって、面\(S_1\)側の極板に蓄えられる電荷を\(Q_{S1}\)、面\(S_2\)側の極板に蓄えられる電荷を\(Q_{S2}\)の大きさはそれぞれ次のように計算できます。
$$ Q_{S1} = \frac{C_{S1}}{V} = ε_{r1} \frac{S_1}{d \times V}$$
$$ Q_{S2} = \frac{C_{S2}}{V} = ε_{r2} \frac{S_2}{d \times V}$$
Q[C]の電荷から出る電気理戦の本数は\(N = \frac{Q}{ε}\)で表されるので、
$$ N_{S1} = \frac{Q_{S1}}{ε_{r1}} = ε_{r1} \frac{S_1}{d \times V \times ε_{r1}} = \frac{S_1}{dV}$$
$$ N_{S2} = \frac{Q_{S2}}{ ε_{r2} } = ε_{r2} \frac{S_2}{d \times V \times ε_{r2} } = \frac{S_2}{dV}$$
問題文より、面\(S_1\)と面\(S_2\)の大きさは同じであるから、
$$ \frac{N_{S1}}{N_{S2}} = \frac{S_1}{S_2} = 1$$
以上のようにして計算することもできる。しかし計算量が多くなってしまうため解答時間を確保するためには、電界と電圧の関係式を覚えておく方が有利といえます。
(イ)面\(S_1\)を貫く電束の総数と面\(S_2\)を貫く電束の総数の比
面\(S_1\)側の電束密度の大きさはポイント②の式より、以下のように表せます。
$$ \begin{align} E_{S1} &= \frac{D_{S1}}{ε_{r1}} \\ D_{S1} &= E \times ε_{r1} \end{align} $$
同様に、面\(S_2\)側の電束密度の大きさは、以下のように表せます。
$$ \begin{align} E_{S2} &= \frac{D_{S2}}{ε_{r2}} \\ D_{S2} &= E \times ε_{r2} \end{align} $$
よって、面\(S_1\)を貫く電束の総数と面\(S_2\)を貫く電束の総数の比は
$$ \frac{D_{S1}}{D_{S2}} = \frac{E \times ε_{r1}}{E \times ε_{r2}} = \frac{ε_{r1}}{ε_{r2}}$$
と表すことができます。
電束\(\psi\)は電気力線\(N\)の\(ε\)倍を用いた考え方
電気力線の本数は(ア)の別解で求めた通り次ようになっている。
面\(S_1\):\(N_{S1} = \frac{S_1}{dV}\) [本]
面\(S_2\):\(N_{S2} = \frac{S_2}{dV}\) [本]
面\(S_1\)を貫く電束の総数と面\(S_2\)を貫く電束の総数は以下のように表せる。
$$ \psi _{S1} = ε_{r1} \times N_{S1} $$
$$ \psi_{S2} = ε_{r2} \times N_{S2}$$
よって、面\(S_1\)を貫く電束の総数と面\(S_2\)を貫く電束の総数の比は、
$$ \frac{\psi_{S1}}{\psi_{S2}} = \frac{ε_{r1} \times \frac{S_1}{dV}}{ε_{r2} \times \frac{S_2}{dV}} = \frac{ε_{r1}}{ε_{r2}}$$
と求めることができます。
(ウ)面\(S_1\)と面\(S_2\)を貫く電束の数の総和
問題文より、極板Aには\(+Q\ [C]\) , 極板Bには\(-Q\ [C]\)の電荷が蓄えられている状態です。\(Q\ [C]\)の電荷から出る電束の数は、\(Q\ [C]\)となります。しかし、平行板コンデンサでは、極板の上面と下面で2等分されてしまいます。この時の様子を図に記すと以下のようになります。
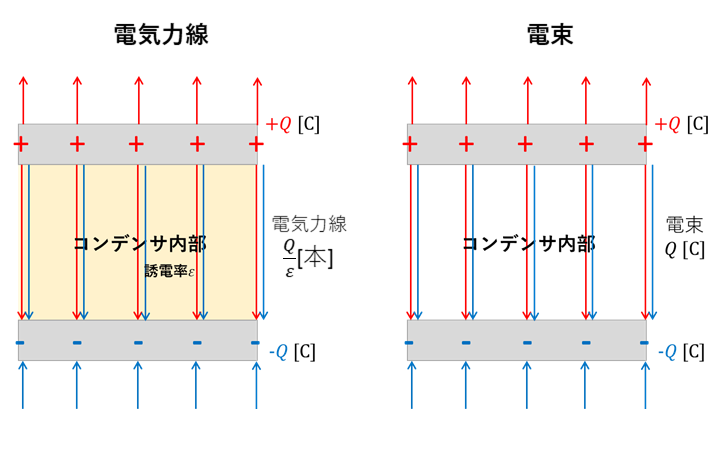
\(+Q\ [C]\)の極板から\(\frac{Q}{2} \ [C]\)、\(-Q\ [C]\)の極板から\(\frac{Q}{2} \ [C]\)の電束が発生するため、電束の総和は\(Q\)[本]となります。
ポイント
平行板コンデンサでは頻出の内容となっているので、必ず覚えておきましょう!
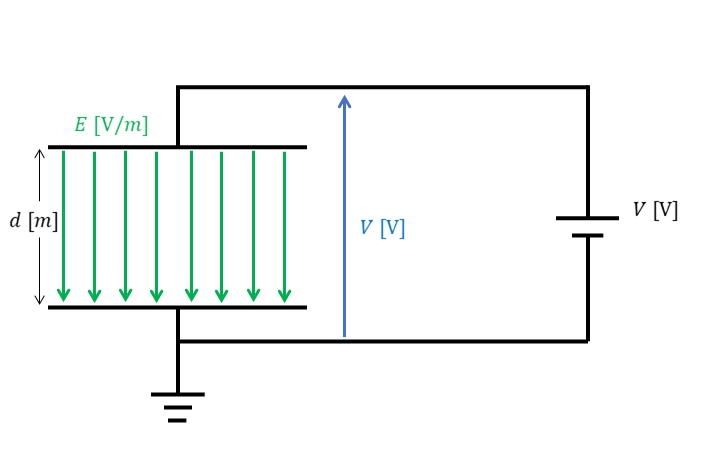
①平行板コンデンサ内の電界の大きさ
平行板コンデンサの金属板上には、電荷が一様に分布しています。また、間にはさまれている誘電体(絶縁体)内部の電気力線密度も一様になり平等電界となります。
この時の電界の大きさは、以下のように表せます。$$ E = \frac{V}{d} $$
②電束密度と電界の大きさ
電束の本数は、誘電率\(ε \ [F/m]\)を無視して考えるため電気力線の本数の\(ε\)倍になります。電気力線の密度は電界の大きさ\( E\ [V/m]\)を表すので、電束の密度(電束密度)\(D\ [C/m^2]\)は電界の大きさ\(E\)の\(ε\)倍になります。$$ D = ε \times E $$











コメント