問題
図のように,極板間の厚さ \(d\ \rm[m]\) ,表面積 \(S\ \rm [m^2]\) の平行板コンデンサ A と B がある。コンデンサ A の内部は,比誘電率と厚さが異なる 3 種類の誘電体で構成され,極板と各誘電体の水平方向の断面積は同一である。コンデンサ B の内部は,比誘電率と水平方向の断面積が異なる 3 種類の誘電体で構成されている。コンデンサ A の各誘電体内部の電界の強さをそれぞれ \(E_{A1}\) , \(E_{A2}\) , \(E_{A3}\) ,コンデンサ B の各誘電体内部の電界の強さをそれぞれ \(E_{B1}\) , \(E_{B2}\) , \(E_{B3}\) とし,端効果,初期電荷及び漏れ電流は無視できるものとする。また,真空の誘電率を \(\varepsilon_0 \ \rm [F/m]\) とする。両コンデンサの上側の極板に電圧 \(V\ \rm[V]\) の直流電源を接続し,下側の極板を接地した。次の(a)及び(b)の問に答えよ。
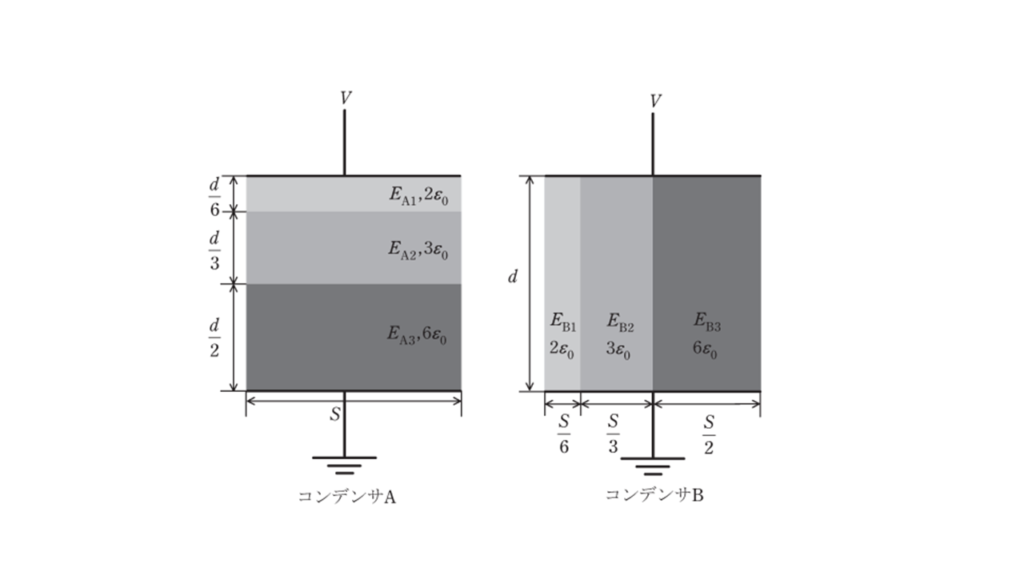
(a) コンデンサ A における各誘電体内部の電界の強さの大小関係とその中の最大値の組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
(1) \(E_{A1} > E_{A2} > E_{A3}\) ,\(\displaystyle \frac{3V}{5d}\)
(2) \(E_{A1} < E_{A2} < E_{A3}\) ,\(\displaystyle \frac{3V}{5d}\)
(3) \(E_{A1} = E_{A2} = E_{A3}\) ,\(\displaystyle \frac{V}{d}\)
(4) \(E_{A1} > E_{A2} > E_A3}\) ,\(\displaystyle \frac{9V}{5d}\)
(5) \(E_{A1} < E_{A2} < E_{A3}\) ,\(\displaystyle \frac{9V}{5d}\)
(b) コンデンサ A 全体の蓄積エネルギーは,コンデンサ B 全体の蓄積エネルギーの何倍か,正しいものを次の(1)~(5)のうちから一つ選べ。
(1) \(0.72\) (2) \(0.83\) (3) \(1.00) (4) \(1.20\) (5) \(1.38\)

解説
答え:(a)-(4),(b)-(2)
(a) コンデンサ A における各誘電体内部の電界の強さを求める
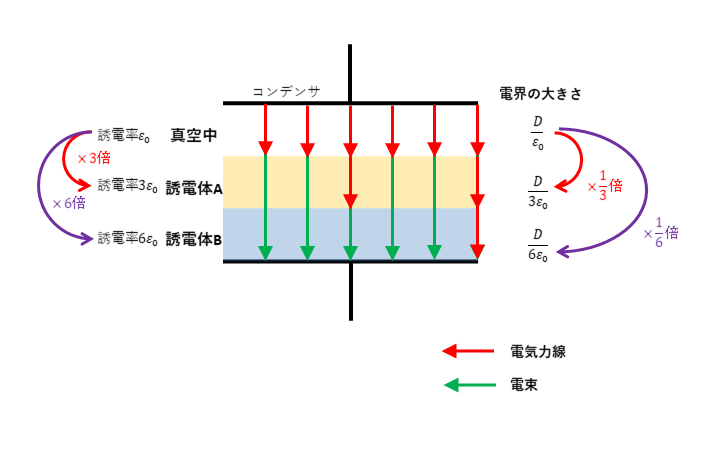
平行板コンデンサ内の電束密度\(D\ [C/m^2]\)の大きさはどの地点でも変化がないため、電界の大きさは誘電率によって決まります(ポイント1)。
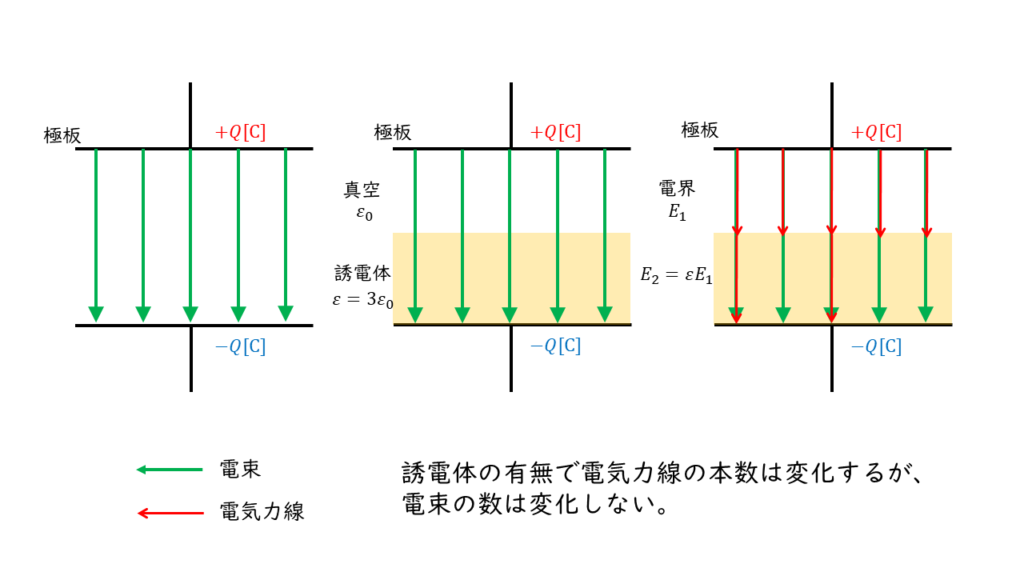
コンデンサAの内部の誘電率は上から順に\(2ε_0\)、\(3ε_0\)、\(6ε_0\)となるため
それぞれの電界の大きさは以下のように表すことができる。
$$ E_{A1} = \frac{D}{2ε_0} \ , \ E_{A2} = \frac{D}{3ε_0} \ , \ E_{A3} = \frac{D}{6ε_0} $$
よって電界の大きさは、\(E_{A1} > E_{A2} > E_{A3} \)となる。
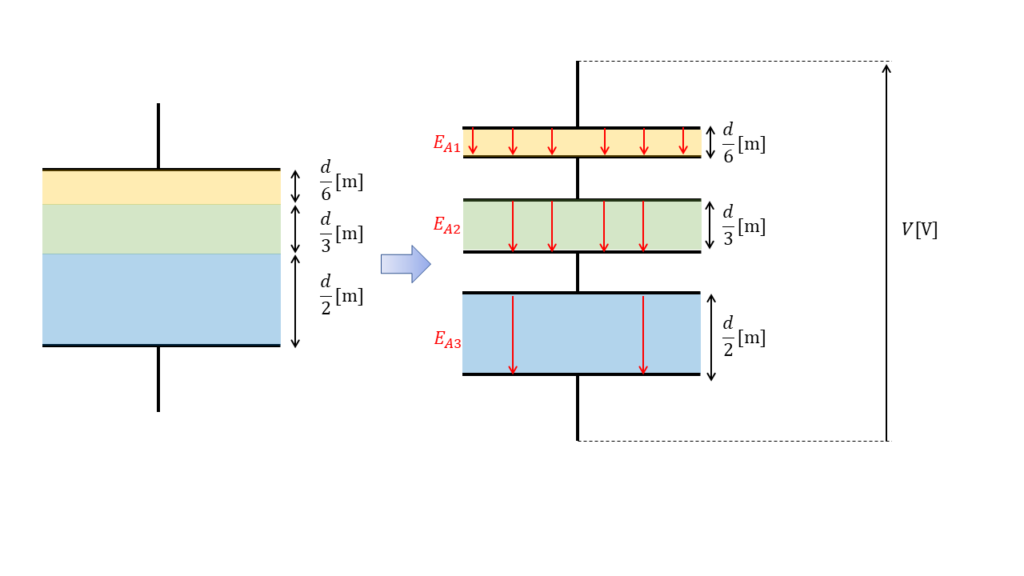
また、この時最大となる電界\(E_{A1}\)の大きさは図より式 \(V = E \times d\) を用いて計算することができる。
$$ V = E_{A1} \times \frac{d}{6} + E_{A2} \times \frac{d}{3} + E_{A3} \times \frac{d}{2}$$
ここで、\(E_{A2} \ , \ E_{A3}\)を\(E_{A1} \)を使った表記に変換する。
$$ E_{A2} = \frac{D}{3ε_0} =\frac{D}{2ε_0} \times \frac{2}{3} = E_{A1} \times \frac{2}{3}$$
$$ E_{A3} = \frac{D}{6ε_0} =\frac{D}{2ε_0} \times \frac{2}{6} = E_{A1} \times \frac{1}{3}$$
電界\(E_A1\)の大きさを計算すると、
$$ \begin{align} V &= E_{A1} \times \frac{d}{6} + E_{A2} \times \frac{d}{3} + E_{A3} \times \frac{d}{2} \\ \\ &= E_{A1} \times \frac{d}{6} + E_{A1} \times \frac{2}{3} \times \frac{d}{3} + E_{A1} \times \frac{1}{3} \times \frac{d}{2} \\ \\ &= E_{A1} \times \frac{d}{6} + E_{A1} \times \frac{2d}{9} + E_{A3} \times \frac{d}{6} \\ \\ &= E_{A1} \frac{3d}{18} + E_{A1} \frac{4d}{18} + E_{A1} \frac{3d}{18} \\ \\ V &= E_{A1} \frac{10d}{18} \\ \\ E_{A1} &= \frac{18V}{10d} = \frac{9V}{5d} \end{align} $$
となります。よって答えは、(4)です。
(b) コンデンサ A 全体の蓄積エネルギーは,コンデンサ B 全体の蓄積エネルギーの何倍か求める
(b)電圧\(V \ [V]\) が一定で加えられているコンデンサに蓄えられるエネルギーの大きさは、静電エネルギーの式\( \displaystyle W = \frac{1}{2}CV^2 \ [J]\)で計算することができます。
コンデンサA側の全体の静電容量の大きさ\(C_A \ [F]\)を求める
初めに、各誘電率の部分での静電容量を計算する。
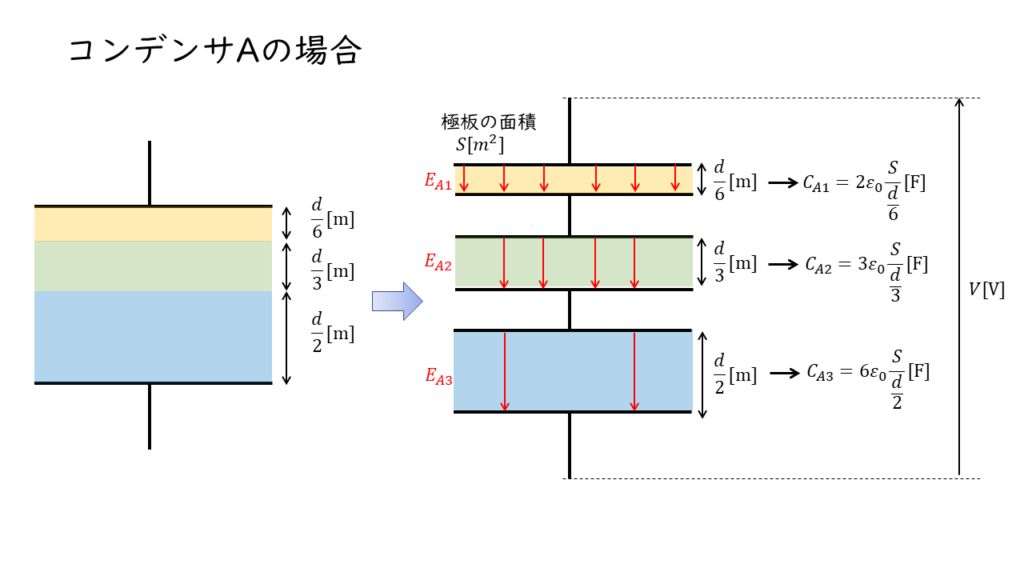
$$ C_{A1} = 2ε_0 \times \frac{S}{\displaystyle \frac{d}{6}} = \frac{2ε_0 S \times 6}{\displaystyle \frac{d}{6} \times 6} = \frac{12ε_0 S}{d} $$
$$ C_{A2} = 3ε_0 \times \frac{S}{\displaystyle \frac{d}{3}} = \frac{3ε_0 S \times 3}{\displaystyle \frac{d}{3} \times 3} = \frac{9ε_0 S}{d} $$
$$ C_{A3} = 6ε_0 \times \frac{S}{\displaystyle \frac{d}{2}} = \frac{6ε_0 S \times 2}{\displaystyle \frac{d}{2} \times 2} = \frac{12ε_0 S}{d} $$
コンデンサA合計の静電容量\(C_{A} \)を計算する。
$$ \begin{align} \frac{1}{C_A} &= \frac{1}{C_{A1}} + \frac{1}{C_{A2}} +\frac{1}{C_{A3}} \\ \\ &= \frac{1}{\displaystyle \frac{12ε_0 S}{d}} + \frac{1}{\displaystyle \frac{9ε_0 S}{d}}+\frac{1}{\displaystyle \frac{12ε_0 S}{d}} \\ \\ &= \frac{d}{12ε_0 S} + \frac{d}{9ε_0 S} +\frac{d}{12ε_0 S} \\ &= \frac{3d}{36ε_0} + \frac{4d}{36ε_0} + \frac{3d}{36ε_0} \\ &= \frac{10d}{36ε_0} \\ C_A &= \frac{36ε_0}{10d} = \frac{18ε_0}{5d} \end{align} $$
コンデンサBの全体の静電容量\(C_B \ [F]\)を求める
初めに、各誘電率の部分での静電容量を計算する。
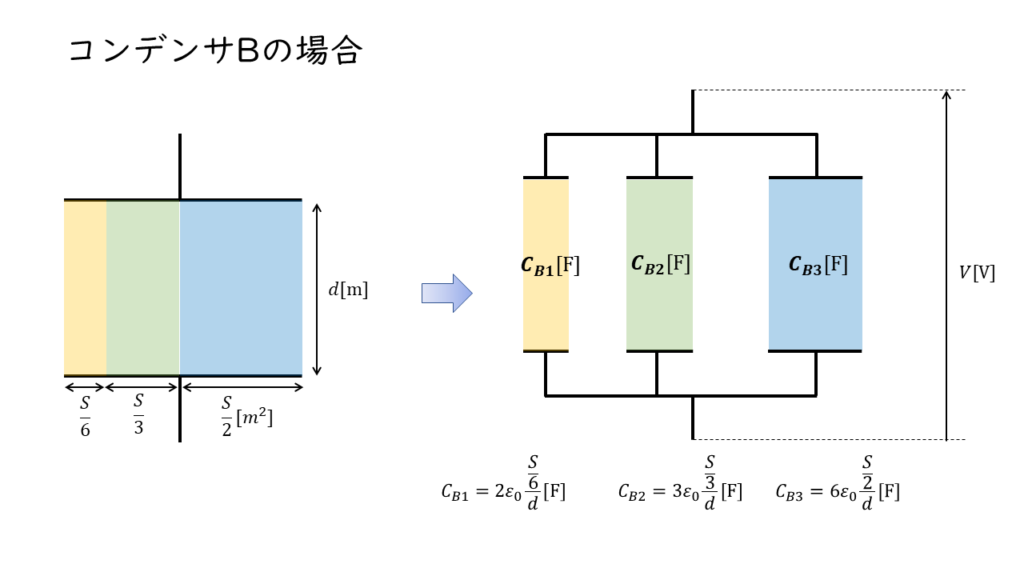
$$ C_{B1} = 2ε_0 \times \frac{\frac{S}{6}}{d} = \frac{2ε_0 S}{6d} = \frac{ε_0 S}{3d}$$
$$ C_{B2} = 3ε_0 \times \frac{\frac{S}{3}}{d} = \frac{3ε_0 S}{3d} = \frac{ε_0 S}{d}$$
$$ C_{B3} = 6ε_0 \times \frac{\frac{S}{2}}{d} = \frac{6ε_0 S}{2d} = \frac{3ε_0 S}{d}$$
コンデンサBの合計の静電容量\(C_B \ [F]\)を計算する。
$$ \begin{align} C_{B} &= C_{B1} + C_{B2} + C_{B3} \\ &= \frac{ε_0 S}{3d} +\frac{ε_0 S}{d} + \frac{3ε_0 S}{d} \\ \\ &= \frac{ε_0 S}{3d} + \frac{3ε_0 S}{3d} + \frac{9ε_0 S}{3d} \\ \\ &= \frac{13ε_0 S}{3d} \end{align}$$
コンデンサAの蓄積エネルギーがコンデンサBの蓄積エネルギーの何倍になるかを計算する
$$ \begin{align} \frac{\displaystyle \frac{1}{2}C_{A}V^2}{\displaystyle \frac{1}{2}C_{B}V^2} &= \frac{\displaystyle\frac{1}{2} \times \displaystyle\frac{18ε_0}{5d} \times V^2}{\displaystyle \frac{1}{2} \times \displaystyle \frac{13ε_0 S}{3d} \times V^2} \\ \\ &=\frac{\displaystyle \frac{18ε_0}{5d}}{\displaystyle \frac{13ε_0 S}{3d}} \\ \\ &=\frac{18ε_0}{5d} \times \frac{3d}{13ε_0 S} \\ \\ &=\frac{18 \times 3}{5 \times 13} = 0.8307 \end{align} $$
よって答えは(2)となります。
ポイント
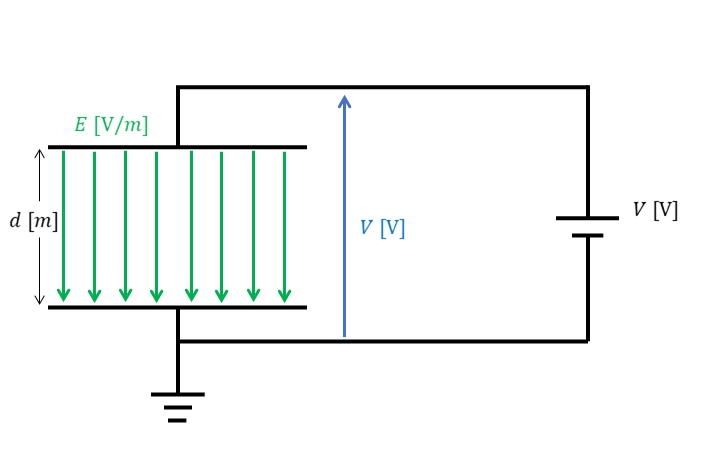
平行板コンデンサ内の電界の大きさ
平行板コンデンサの金属板上には、電荷が一様に分布しています。また、間にはさまれている誘電体(絶縁体)内部の電気力線密度も一様になり平等電界となります。
この時の電界の大きさは、以下のように表せます。$$ E = \frac{V}{d} $$
電束密度と電界の大きさ
電束の本数は、誘電率\(ε \ [F/m]\)を無視して考えるため電気力線の本数の\(ε\)倍になります。電気力線の密度は電界の大きさ\( E\ [V/m]\)を表すので、電束の密度(電束密度)\(D\ [C/m^2]\)は電界の大きさ\(E\)の\(ε\)倍になります。$$ D = ε \times E $$
平行板コンデンサ容量\(C\ [F]\)の求め方
極板の面積を\(S\ [m^2]\)、極板間の距離を\(d\ [m]\)、誘電率を\(ε\ [F/m]\)とすると、コンデンサの静電容量\(C\ [F]\)は次のように表すことができる。
$$ C = ε \times \frac{S}{d} \ [F] $$
コンデンサ容量の合成
直列接続の場合
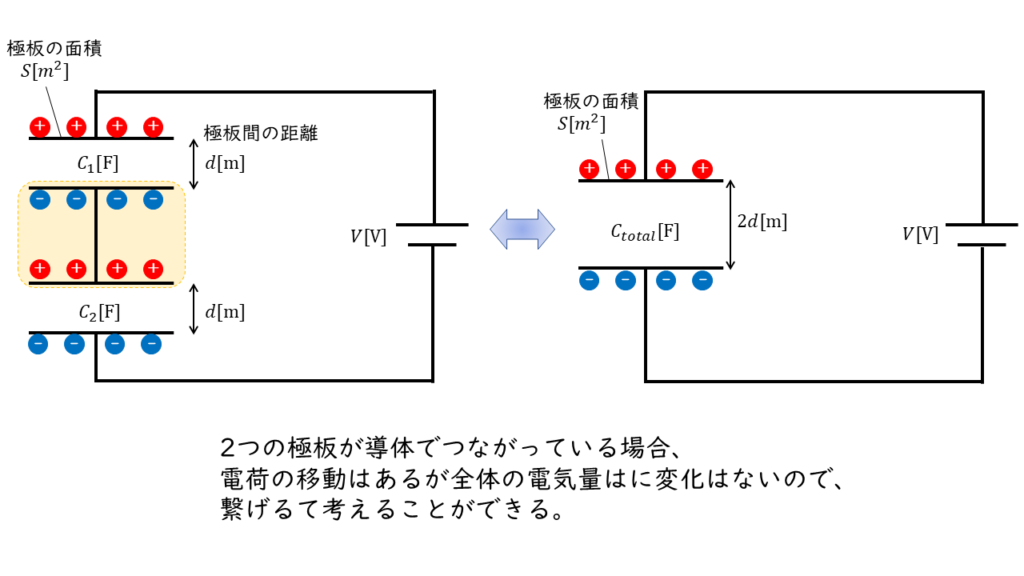
$$ \begin{align} \frac{1}{C_{total}} &= \frac{1}{C_1} + \frac{1}{C_2}\\ \\ &= \frac{C_2}{C_1 \times C_2} + \frac{C_1}{C_2 \times C_1} \\ \\ &= \frac{C_2 + C_1}{C_1 \times C_2} \\ \\ C_{total} &= \frac{C_1 \times C_2}{C_1 + C_2} \end{align} $$
並列接続の場合
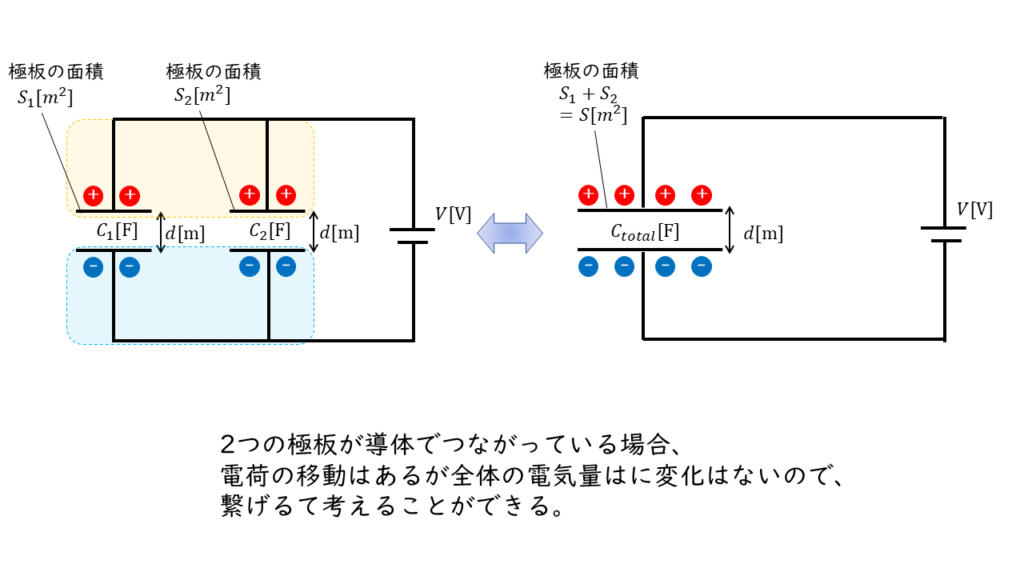
$$ C_{total} = C_1 + C_2 $$
静電エネルギーの大きさ
平行板コンデンサの静電エネルギー\(W\ [J]\)の大きさは静電容量\(C\ [F]\)と電位差\(V\ [V]\)から以下の様に計算することができます。
$$ W = \frac{1}{2} C V^2 $$











コメント