私たちが普段何気なく使用している電気の大半は交流と呼ばれる電気です。
交流の電気の特徴は常に波打つようにプラスとマイナスが入れ替わっています。プラスとマイナスを行き来する際、必ず一度0を通ります。
そのため、電気の流れを遮断する場合も直流の電気に比べて容易に行うことができるのも利点の1つです。
また、電機を遠くへ送る場合、送電線などの電気抵抗により損失が発生するため、損失の低減のために電圧を数千、数万[V]まで高い値に変換します。電圧の変換には変圧器が用いられますが、これは交流でのみ使用可能です。
電気を扱う上で交流に関する知識は必須となります。考え方や計算方法に癖がありますが、数をこなすうちに慣れていきます。
- 交流の起電力
- 周波数と角周波数
- 瞬時値、平均値、実効値
- 位相と位相差
交流とは
交流とは時間とともに大きさと向きが周期的に変化する電気の流れのことを言います。

普段何気なく使っているコンセントからの電気は全て交流です。
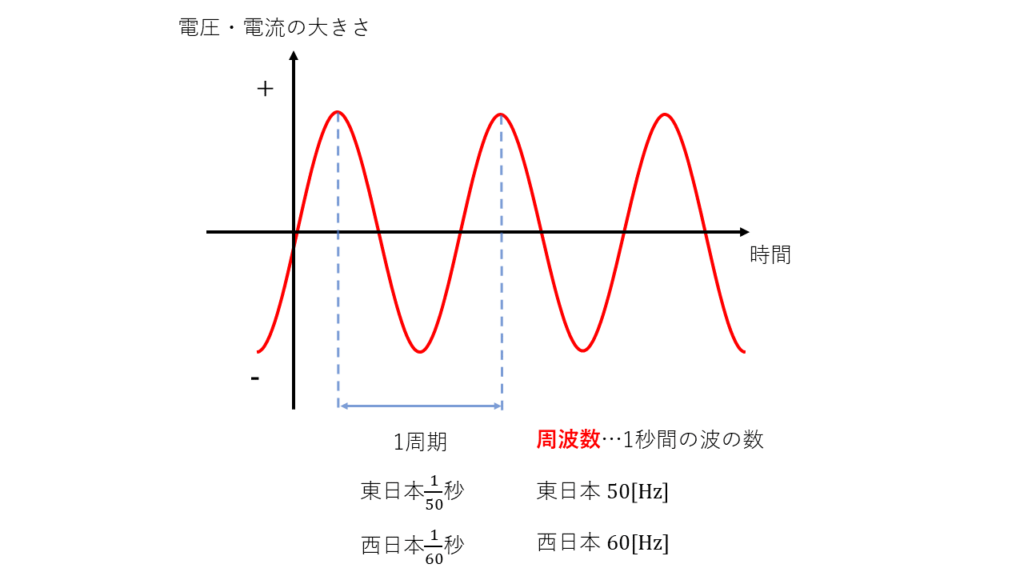
周期的とは、ある一定の時間がたつとまったく同じことが起こることを指しています。
電気の分野では電流や電圧の向き(プラス、マイナス)と大きさが一定の波を作るように変化しています。
交流の起電力(電圧源)
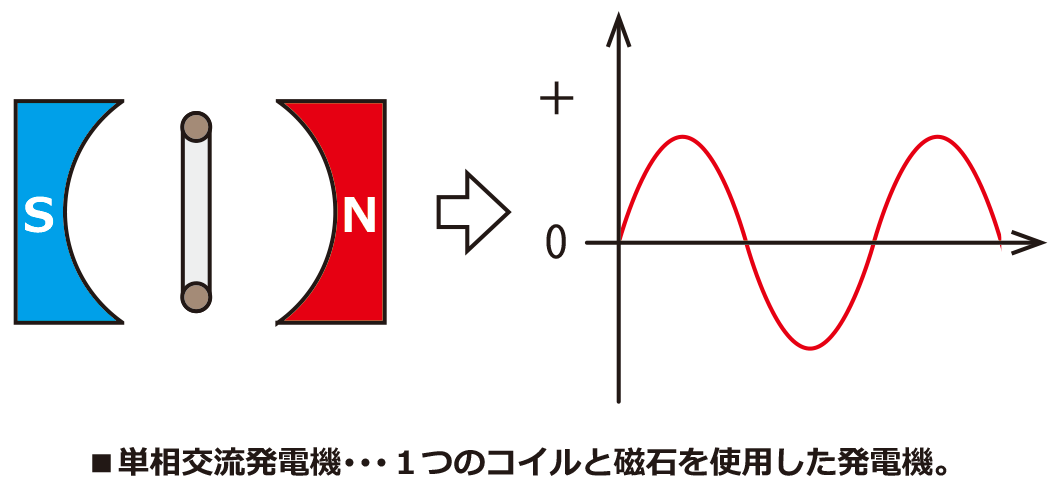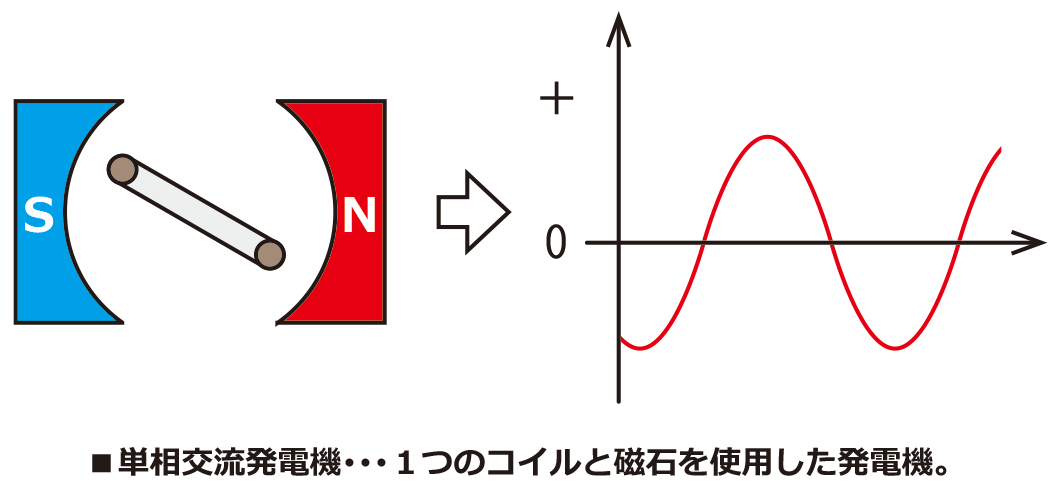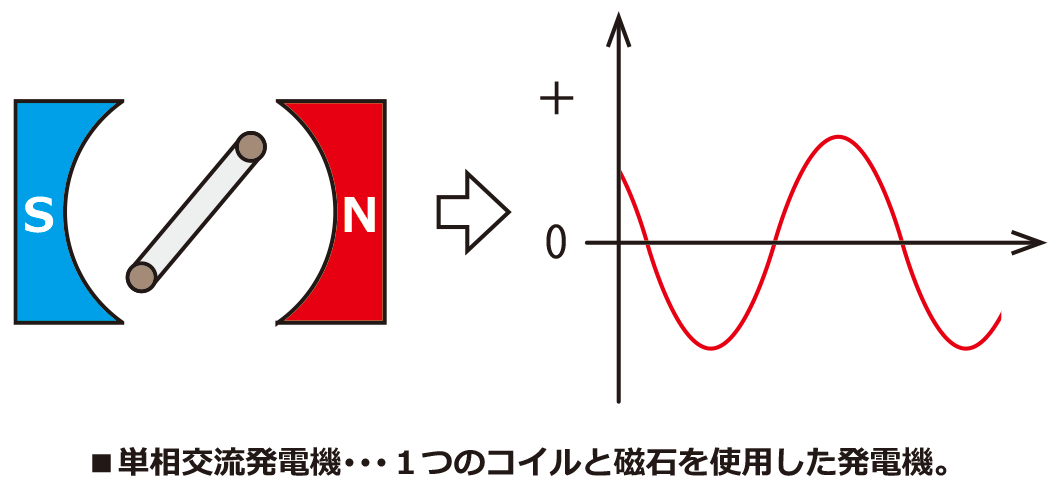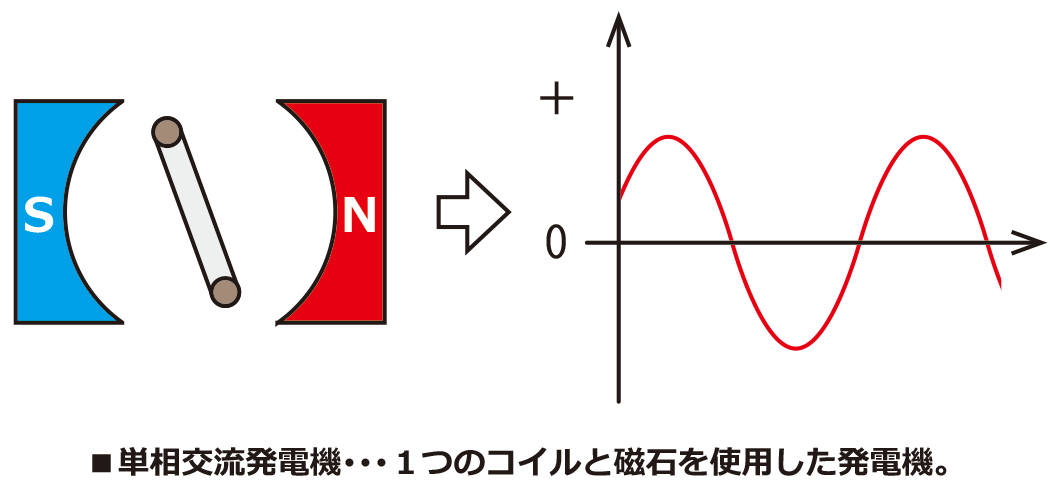
交流の電気は発電機を回転させることによって作られています。
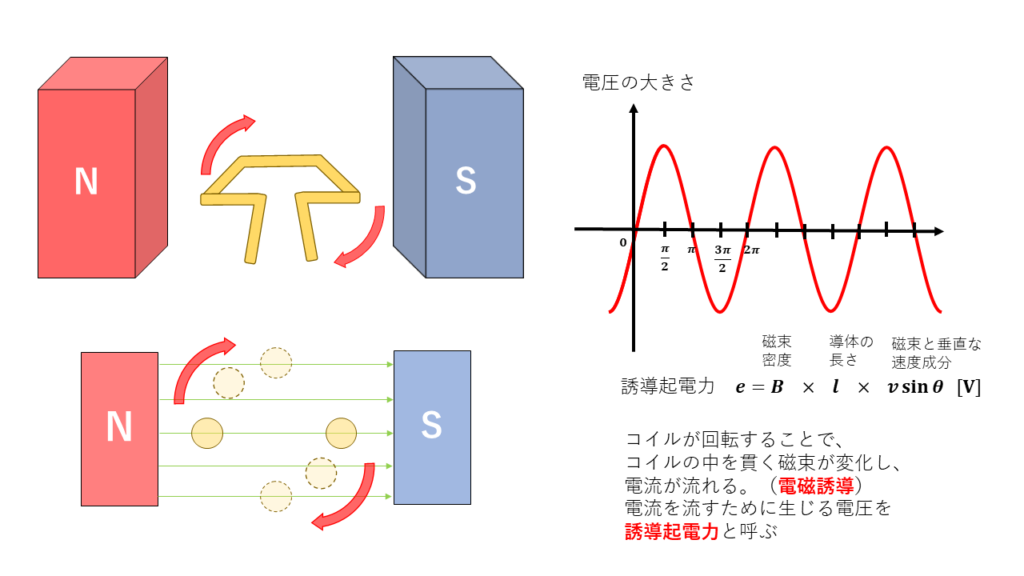
発電の原理としては、電磁気の分野で学習した電磁誘導を利用しています。磁界の中に置いたコイルを回転させることでコイルに起電力を生じさせています。
電源電圧(コイルの誘導起電力)は\(\sin\theta\)を使って表すことができるので、正弦波交流と呼びます。
この時の電圧(誘導起電力)の大きさは以下の式で求めることができます。
\( e = B \times I \times v\sin\theta \)
周波数と角周波数
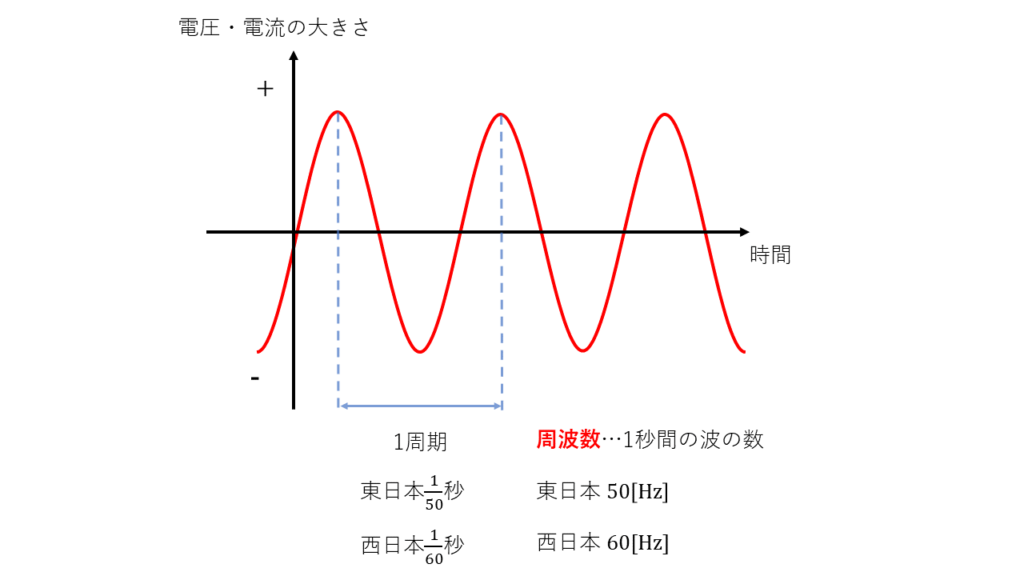
周期:山の頂上から次の山の頂上または、谷から次の谷までの間の時間を周期と呼びます。
記号は \(T\)、単位は \(s\)(秒)を使用します。
1つの波が始まってから終わるまでにどのくらいの時間が必要かを示したものが周期です。
周波数:1秒間に繰り返される周期の回数を周波数と呼びます。
記号は \(f\)、単位は\(Hz\)(ヘルツ)を使用します。
上図を例にすると、東日本の電源電圧は1秒間で50回波が発生するので50[Hz]になります。
\( f = \displaystyle \frac{1}{T} \)
\(f\):周波数[Hz]
\(T\):周期[s]
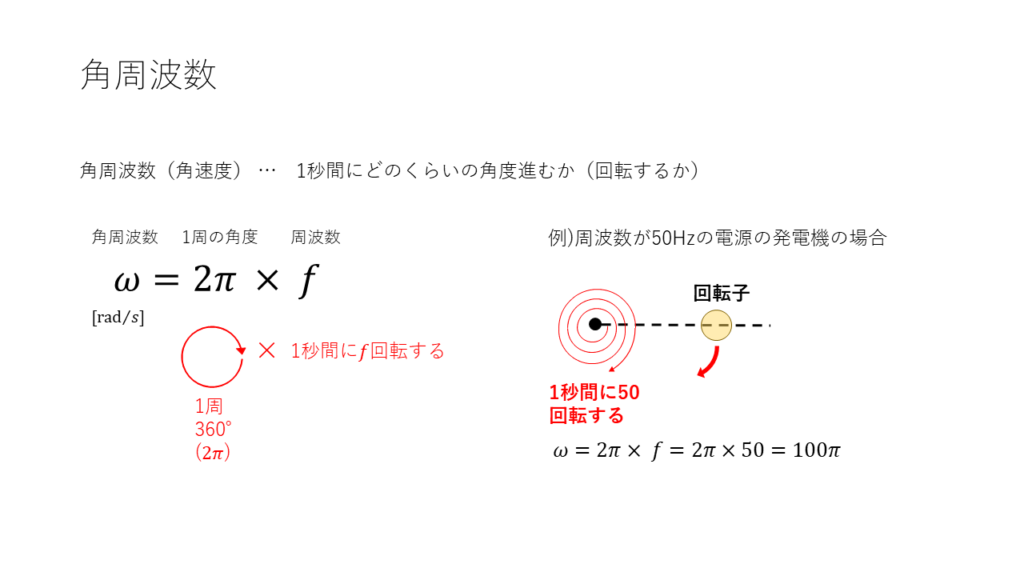
角周波数…1秒当たりにどのくらいの角度を進むのか(何回転するのか)を表したのも
記号は\(\omega\)、単位は[rad/s](ラジアン毎秒)を使用します
瞬時値、平均値、実行値
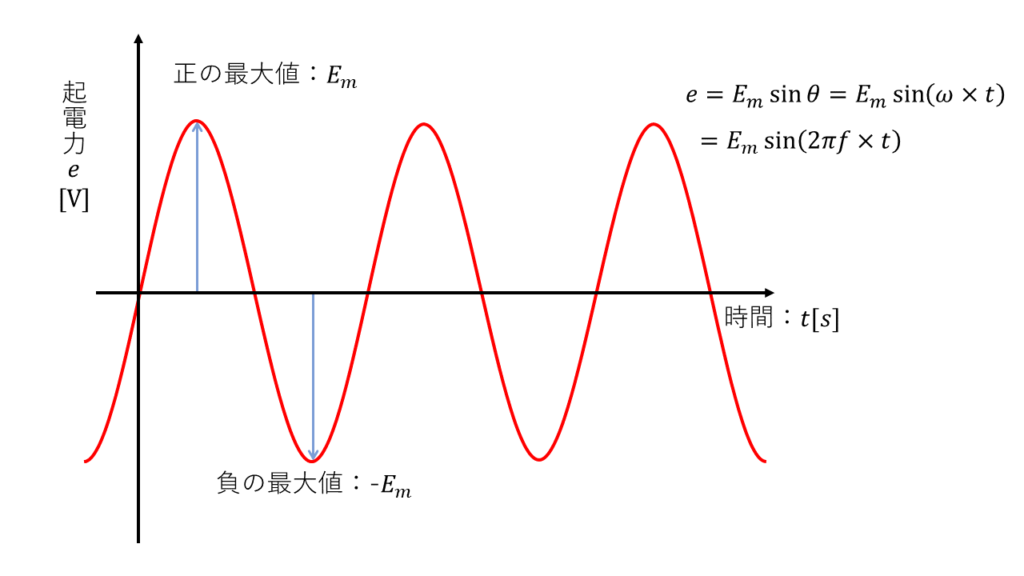
瞬時値…ある時間での値
最大値…瞬時値のうち最も大きくなる値のことを最大値という
\(\begin{align} e &= E_m \sin\theta \\ &= E_m \sin \left( \omega t \right) \\ &= E_m \sin \left( 2 \pi f t \right) \ \rm[V] \end{align} \)
交流は常に値が変化し続けるため、「〇〇[V]です」と断言することができません。そこで、目安として平均値や実効値が使われています。
平均値
交流では、半周期(0度から180度)までの値の平均を平均値といいます。
平均値 \(V_{av} = \displaystyle \frac{2}{\pi} \times 最大値 V_m\)
実効値
実効値とは、交流を直流と同じように見立てたときの値のことを言います。
実効値は直流と同じように一定の値として計算に使用することができるのでとても便利なのです。
\( E = \displaystyle \frac{最大値\ E_m}{\sqrt{2}} \) [V]
実効値の公式は以下の手順で求められています。
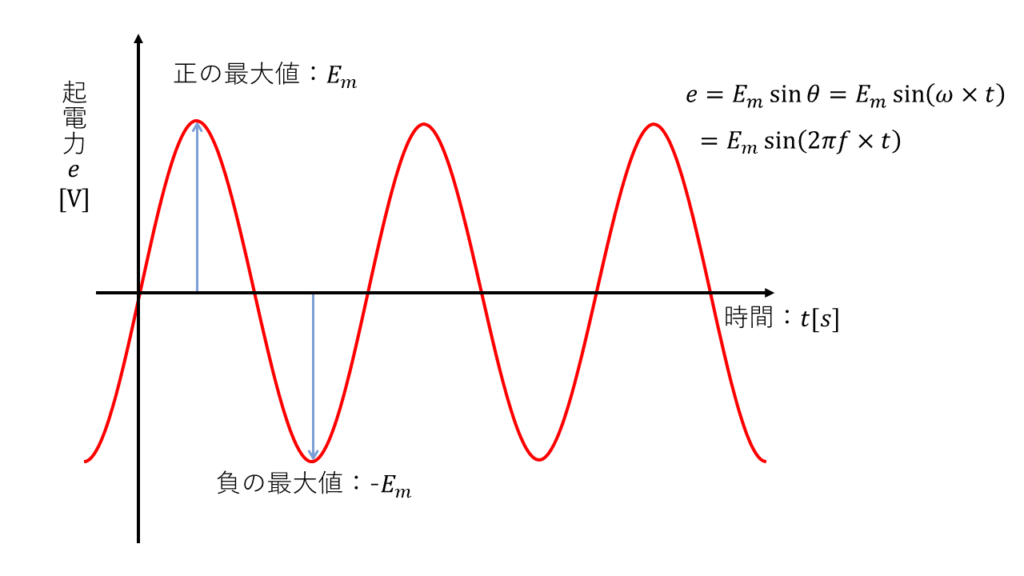
正弦波交流を2乗して、全てプラスの値にします。
\(e^2 = E_m ^2 \times sin^2 (\omega t) \)
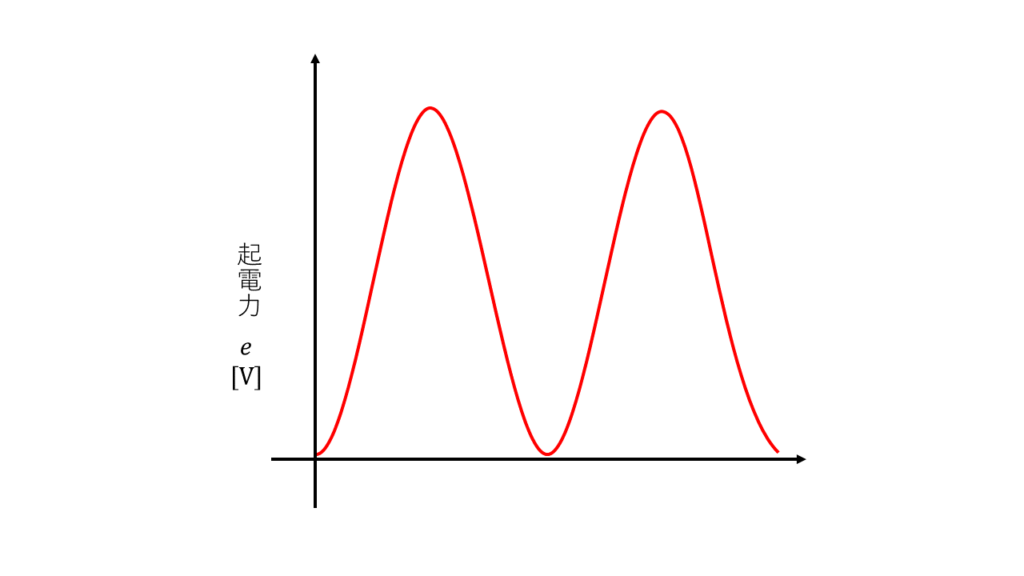
この全てプラスにしたときの平均値を計算します。
平均値 \(E^2 = \displaystyle \frac{E_m^2}{2}\)
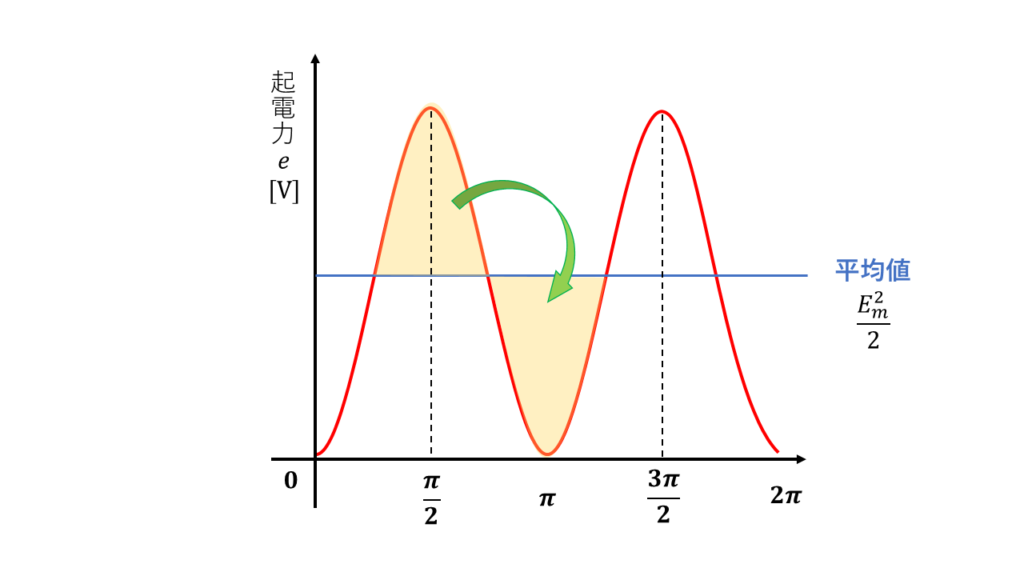
計算しやすくするために2乗していたので、両辺に平方根(ルート) をかけてもとに戻します。
実効値 \(E = \sqrt{\displaystyle \frac{E_m^2}{2}}= \displaystyle \frac{E_m}{\sqrt{2}}\)
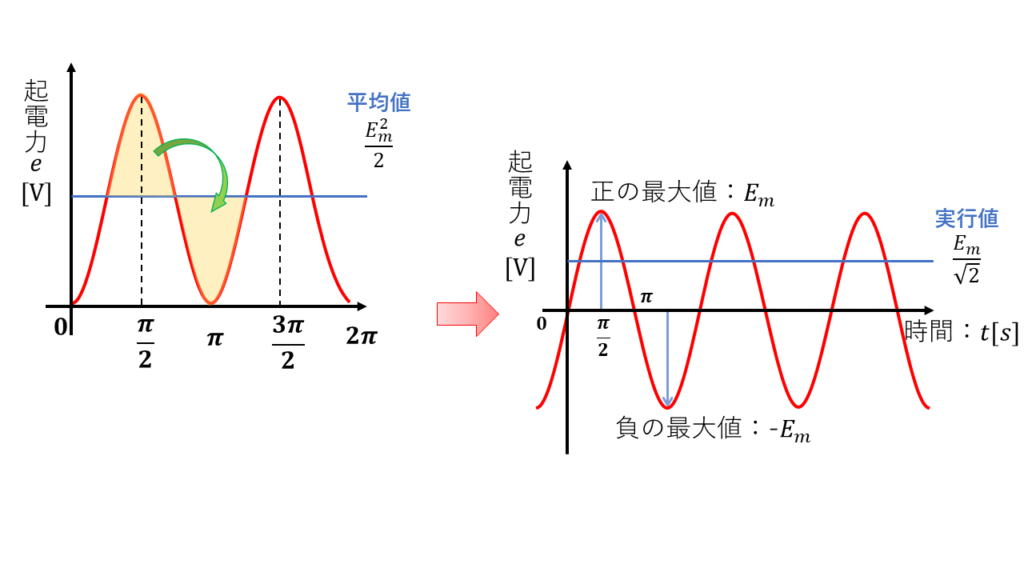
交流回路の計算では主に実効値を利用します。導出過程はともかく、最大値を\(\sqrt{2}\)で割り算することで実効値が得られることは覚えておきましょう!!
位相と位相差
交流回路を考えるうえで実行と同じく重要なのが位相です。位相とは、\(\sin(\omega t)\) の波の形を決める\(\omega t\)のことを指します。一般的には、\(\sin(\omega t)\)の状態を基準に考えます。
\( e=E_m \sin(\omega t) \)
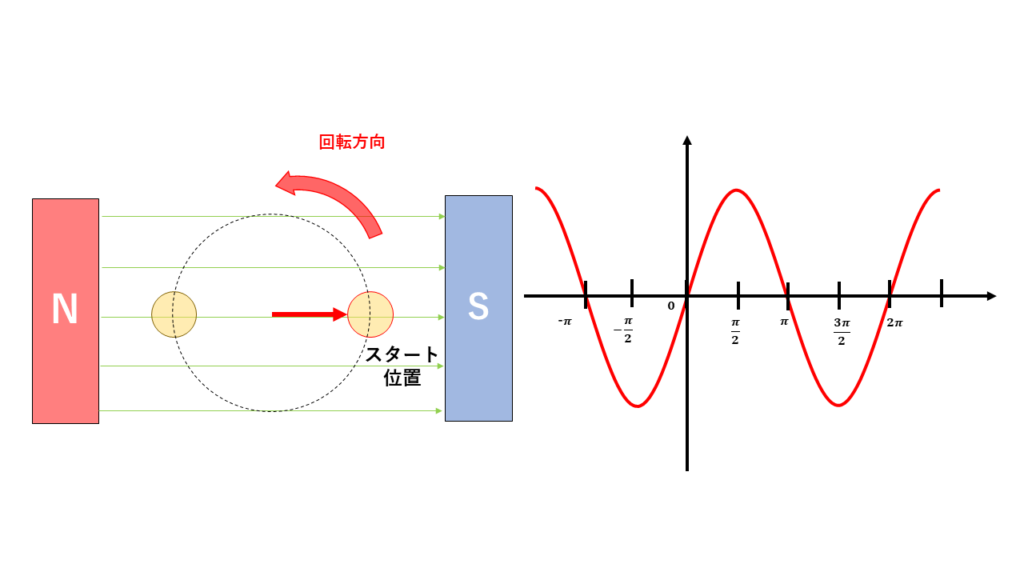
次に、スタート地点を90度右にずらした場合についてみてみましょう。
この時、初めに紹介した波の波形と同じになるためには90度余分にコイルが回転しなければなりません。よって、誘導起電力の波形も先ほどのものと比べるとピークが来るまでに90度遅れている形になります。
\( e=E_m \sin(\omega t+ \displaystyle \frac{\pi}{2}) \)
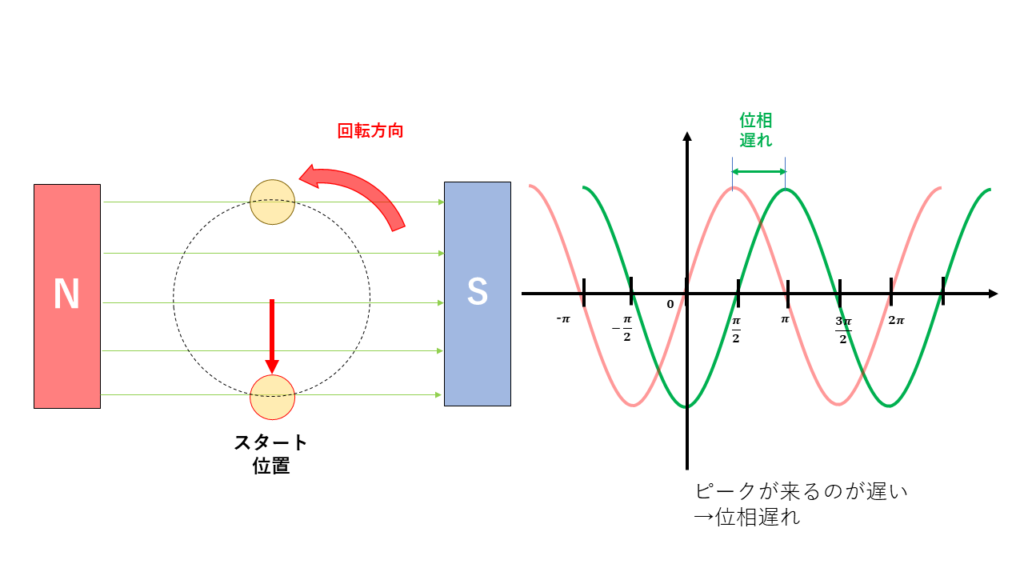
基準の波形からのズレを位相差と呼びます。特に、上図のようにピークが遅れる場合を「位相が遅れている」といいます。
では、最後にスタート地点を90度左にずらした場合ついて考えます。
先ほどとは逆に、今度はピークが来るのが90度早くなるので式としては
\( e=E_m \sin \left( \omega t+ \displaystyle \frac{\pi}{2} \right) \)
となります。グラフにしますと以下のようになります。
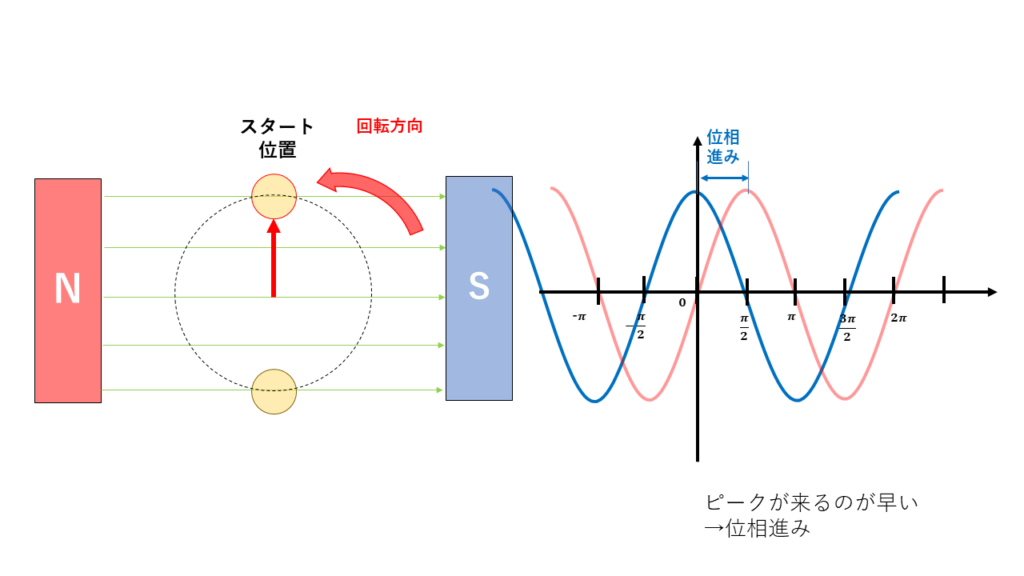
ピークが来るのが早いのでこの状態を「位相が進んでいる」といいます。
まとめ
交流電圧の瞬時値
\( e=\sqrt{2}E \sin \left( \omega t+\phi \right) \) [V]
交流電流の瞬時値
\( i =\sqrt{2}I \sin \left( \omega t+\phi \right) \) [A]
\(\sqrt{2}\)は最大値\(E_m , I_m\)は実効値\(E , I\)の\(\sqrt{2}\)倍のためものです。
\(\phi\)は初期位相(スタート地点)





コメント