R-L-C回路

R , L , C の働き

交流回路では、抵抗ＲだけでなくインダクタンスＬや静電容量Ｃも電流の流れを妨げます。

また、交流回路では電流の大きさだけでなく、電圧と電流の位相差についても考える必要があります。

それでは、抵抗R、インダクタンスL、静電容量Cのそれぞれの働きについてみていきましょう。

抵抗R

交流電圧\(\dot{V}\)を抵抗\(\mathrm{R}\)のみの回路に加えると、生じる電流は電圧と同位相になります。

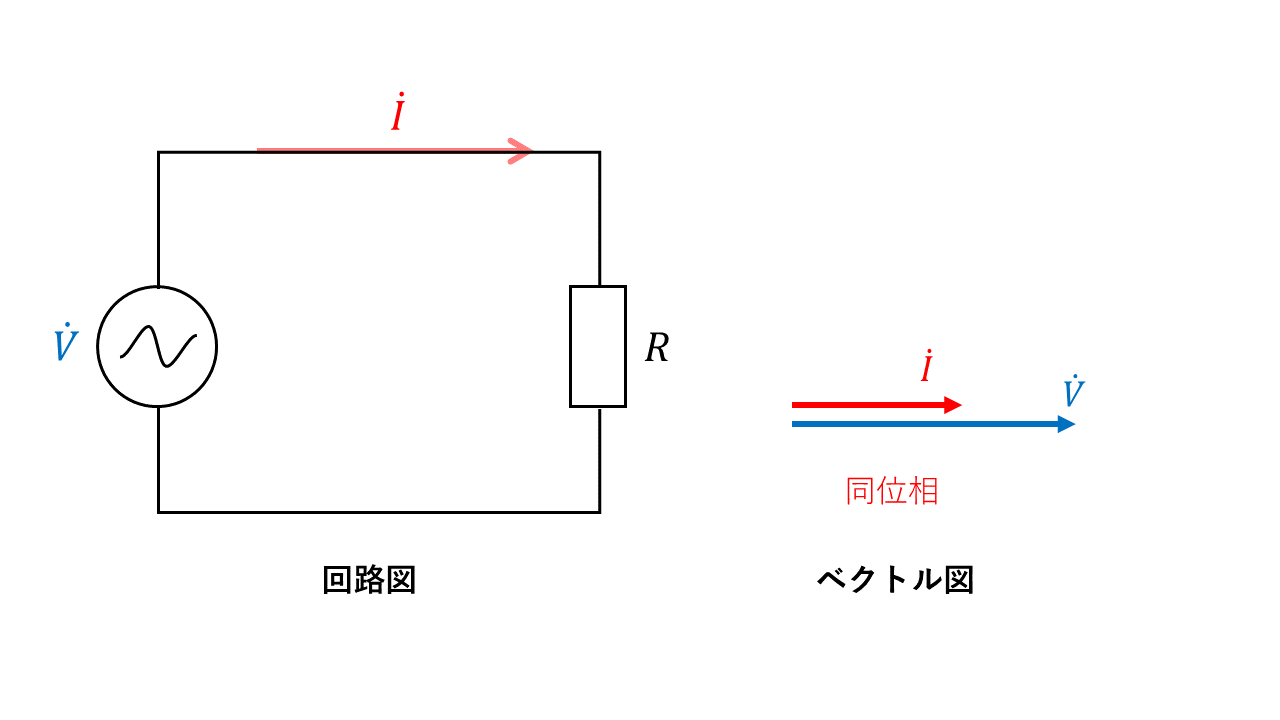
電流の大きさ\(I\)[A]（実効値）は電圧の実効値を\(V\)[V]、抵抗の大きさを\(\mathrm{R}\)[Ω]とすると

$$I = \frac{V}{\mathrm{R}}$$

と表すことができます。これは、瞬時値にも応用することができます。

正弦波交流\(v=100 \sqrt{2}\sin\omega t\)[V]の電圧を、抵抗\(\mathrm{R}=20\)[Ω]のみの回路に印加したときの電流\(i\)[A]は、以下のように求めることができます。

$$\begin{align} i & = \frac{v}{\mathrm{R}} \\ &= \frac{100 \sqrt{2}\sin\omega t}{20} \\ &= 5 \sqrt{2}\sin\omega t \end{align}$$

インダクタンスL

交流電圧\(\dot{V}\)をインダクタンスLのみの回路に加えると、生じる電流は電圧より\( \displaystyle \frac{\pi}{2}\)遅れた位相になります。

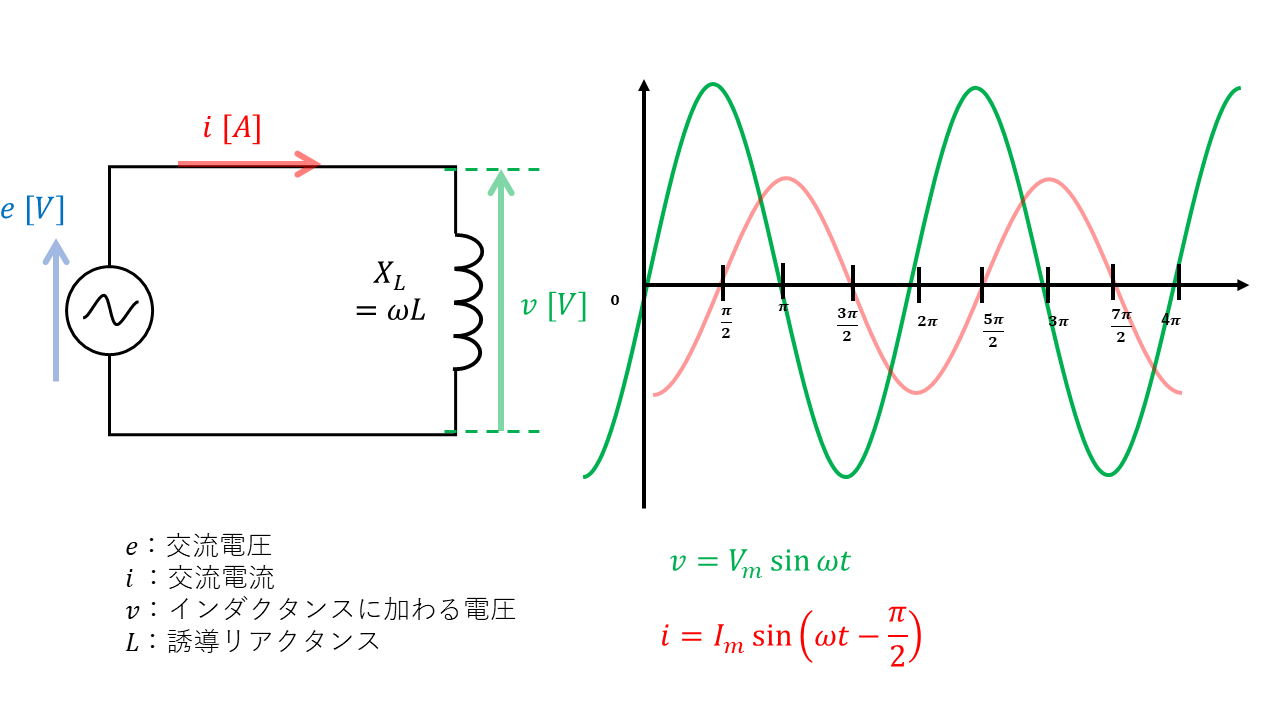
交流回路では電流が常に変化しているため、誘導起電力によって電源電圧とは逆向きの起電力（電圧）が発生し、電流の流れを妨げています。

逆起電力\(e = -L \displaystyle \frac{\Delta i}{\Delta t}\) [V]で表され、電流の変化が速い（周波数 \(f\) が大きい）ほど、インダクタンスLが電流の流れを邪魔する働きが大きくなります。

よって、交流回路ではコイル（インダクタンスL）は周波数によって大きさを変える抵抗とみなすことができます。これを、誘導リアクタンス：\(X_L\)[Ω]といいます。

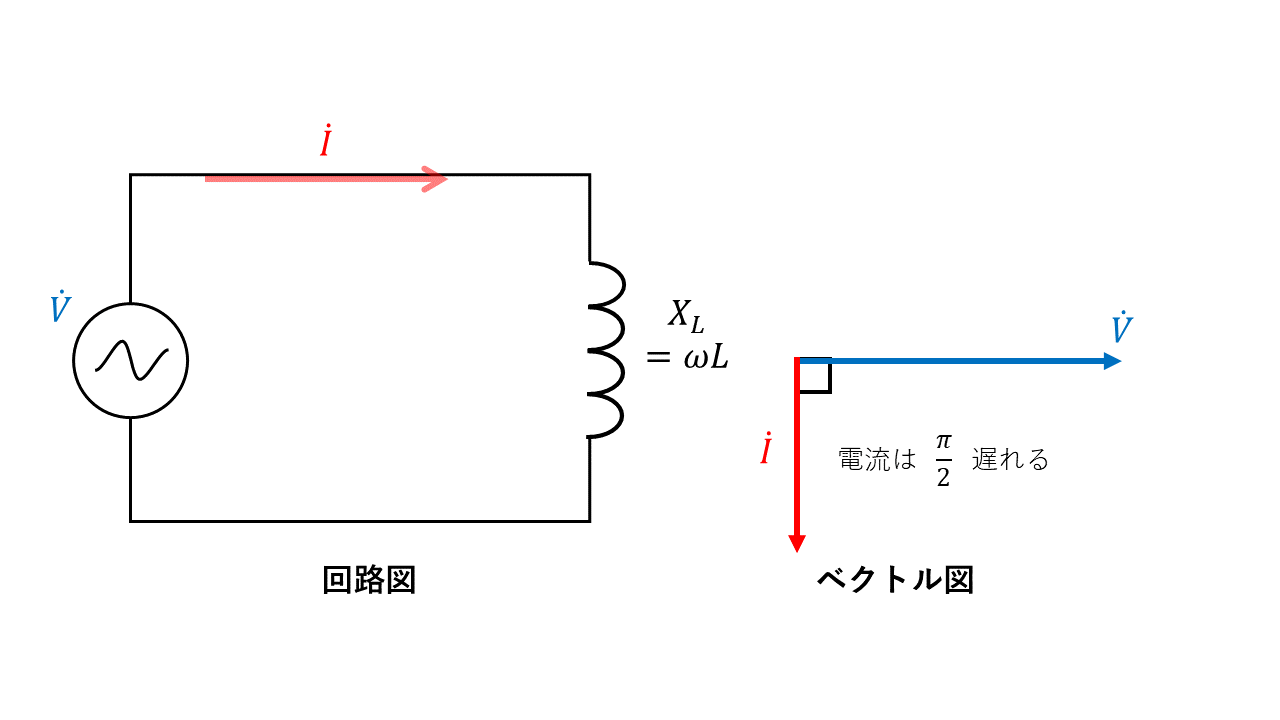
誘導リアクタンスを用いて回路を流れる電流の実効値を求める時は、オームの法則を使って以下のように計算できます。

$$ I = \frac{V}{X_l} = \frac{V}{2\pi f L}$$

静電容量C

交流電圧\(\dot{V}\)を静電容量Cのみの回路に加えると、生じる電流は電圧より\(\displaystyle \frac{\pi}{2}\)進んだ位相になります。これはコンデンサの持つ充放電作用によるものです。

わかりやすい覚え方としては、コンデンサ（静電容量）はコイル（インダクタンス）とまったく逆の働きをすると覚えておくといいです。

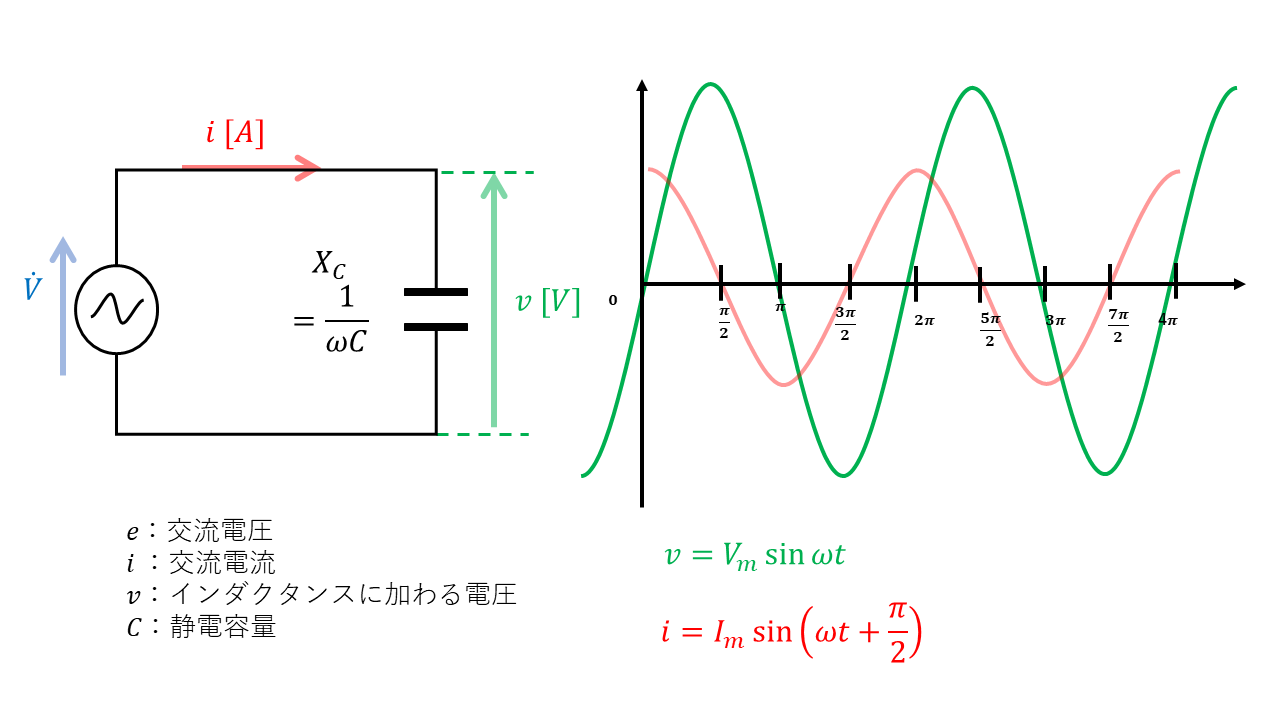
コイルと逆の働きをするので、静電容量による電流の妨げは以下のように表すことができます。

$$ X_C = \frac{1}{2\pi f C} = \frac{1}{\omega C}$$

\(X_C\)[Ω]は容量リアクタンスと呼びます。

R-L-C直列回路

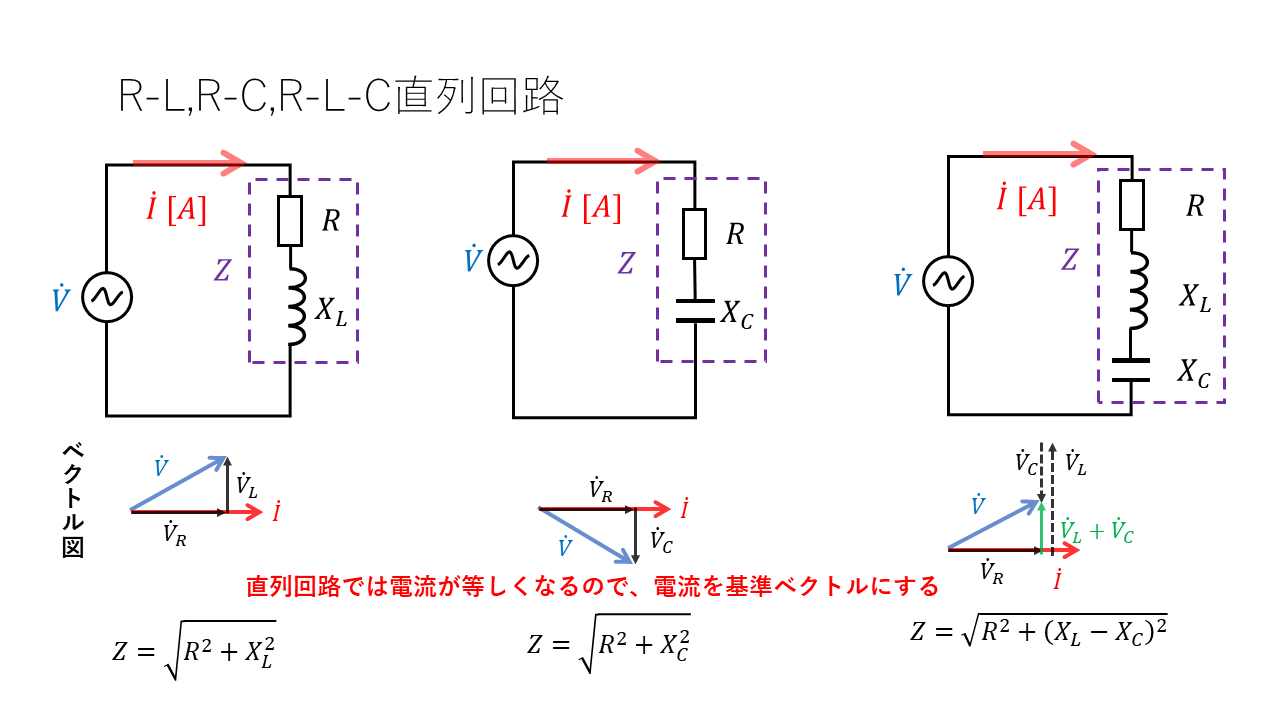
交流回路では、抵抗R、インダクタンスL、静電容量Cによって電圧・電流の位相が変化するため、大きさを求める際にはベクトルで考える必要があります。

直列回路の場合には、電流の値が回路のどの点でも等しくなる性質があるので、電流を基準のベクトルとして考えます。

R-L直列回路

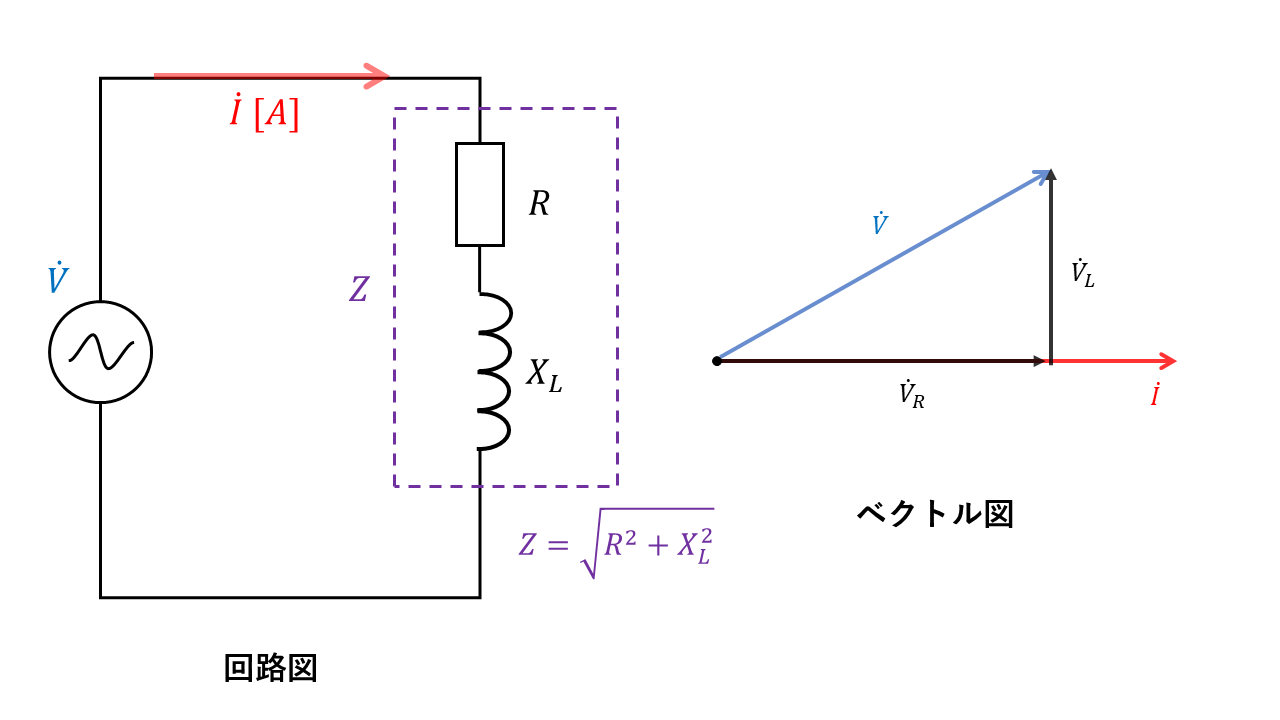
抵抗R、インダクタンスLにかかる電圧の和は電源電圧の大きさと同じになります。

$$\dot{V}=\dot{V_R} + \dot{V_L}$$

電源電圧Vの大きさ（\(dot{V}\)の長さ）は、ピタゴラスの定理より

$$ V = \sqrt{V_R^2 + V_L^2}$$

で求めることができる。

抵抗R、インダクタンスLにかかる電圧の大きさは、[Ω]×[A]で求めることができるので、

$$ \begin{align} V &= \sqrt{(RI)^2 + (X_L I)^2} \\ &=\sqrt{I^2(R^2 + X_L^2)} \\ &=I \sqrt{R^2 + X_L^2} \end{align} $$

以上のように計算することができます。ここで、\(\sqrt{R^2 + X_L^2}\)は交流回路における合成抵抗のようなものと考えることができ、インピーダンス：\(\mathrm{Z}\)[Ω]と呼びます。

R-C直列回路

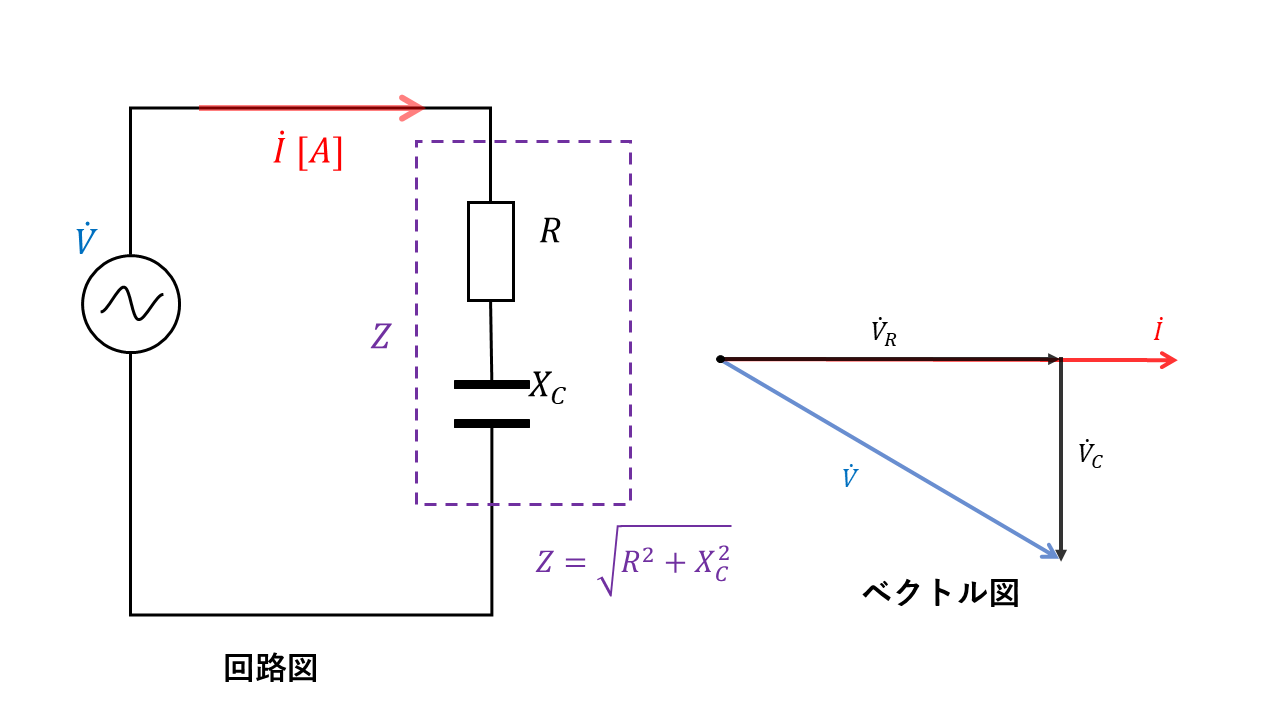
抵抗Rと静電容量Cのみからなる回路も先ほどの抵抗RとインダクタンスLの場合と同様に考えることができます。

$$\dot{V}=\dot{V_R} + \dot{V_C}$$

電源電圧Vの大きさ（\(dot{V}\)の長さ）は、ピタゴラスの定理より

$$ V = \sqrt{V_R^2 + V_C^2}$$

で求めることができる。

抵抗R、静電容量Cにかかる電圧の大きさは、[Ω]×[A]で求めることができるので、

$$ \begin{align} V &= \sqrt{(RI)^2 + (X_C I)^2} \\ &=\sqrt{I^2(R^2 + X_C^2)} \\ &=I \sqrt{R^2 + X_C^2} \end{align} $$

R-L-C直列回路

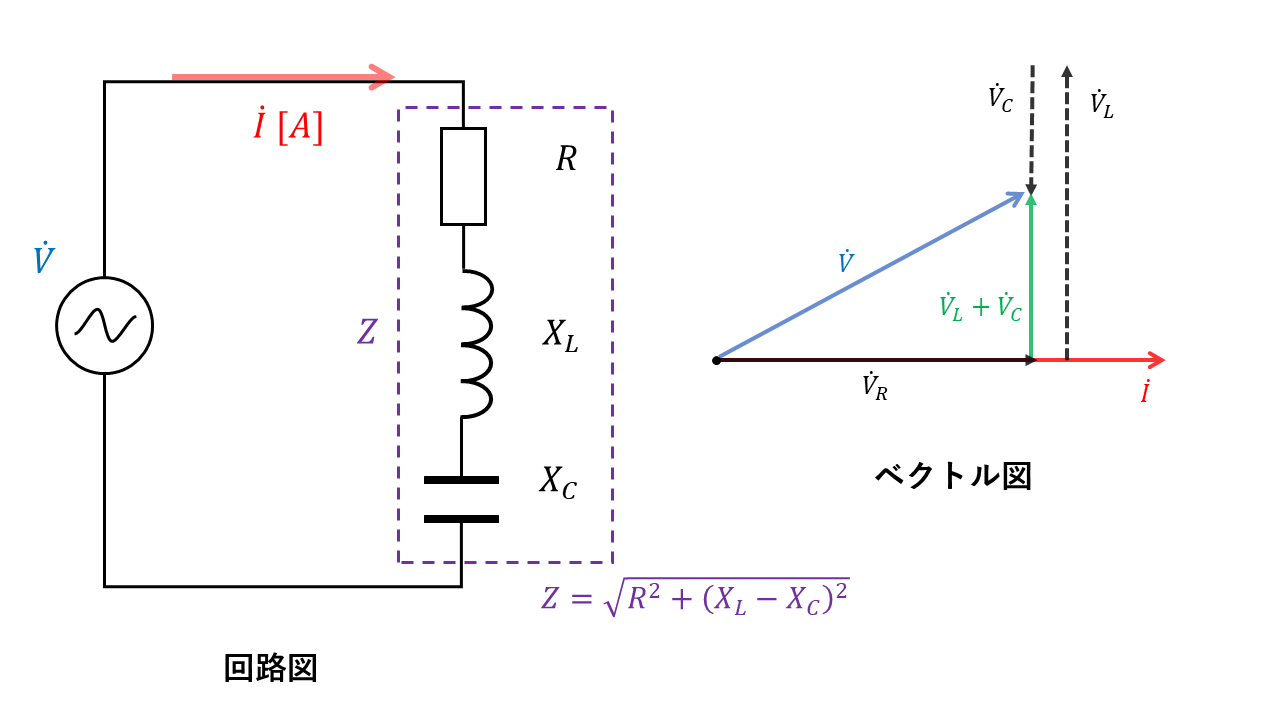
最後に、R-L-Cすべてが直列に接続された回路について解説します。

基本の計算方法は変わりません。注意点としては、インダクタンスLと静電容量Cは逆の働きをするという点です。数式で表す場合、一般的に遅れ（インダクタンス）の方を+で考えます。

$$\dot{V}=\dot{V_R} + \dot{V_L} + \dot{V_C}$$

ここで注意するのが、\(\dot{V_L} + \dot{V_C}\)の長さ（絶対値）は\(\vert V_L – V_C \vert \)とすることです。

電源電圧Vの大きさ（\(\dot{V}\)の長さ）は、ピタゴラスの定理より

$$ \begin{align}V &= \sqrt{V_R^2 + (V_L – V_C)^2} \\ V &= \sqrt{(RI)^2 + (X_L I – X_C I)^2} \\ &=\sqrt{I^2{R^2 + (X_L – X_C)^2}} \\ &=I \sqrt{R^2+ ( X_L – X_C)^2} \end{align} $$

R-L-C並列回路

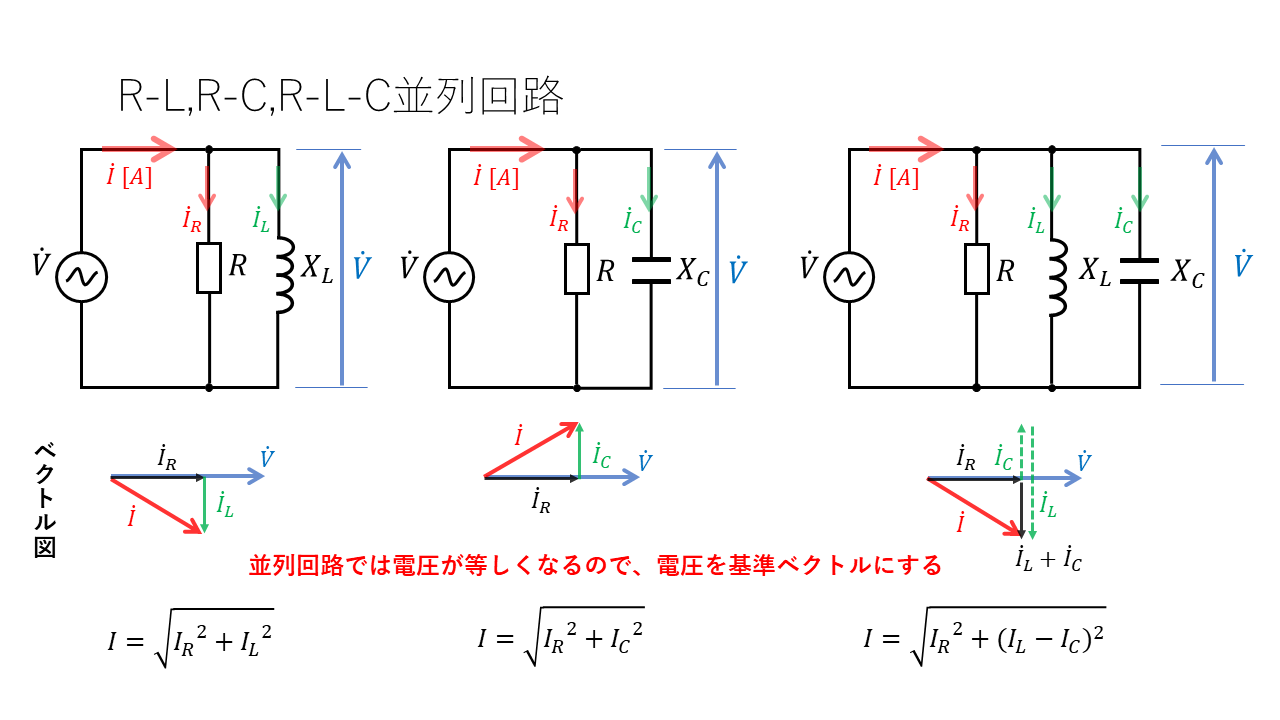
R-L-C並列回路では、並列回路の特性である並列接続の部分にかかる電圧の値は等しくなることを利用して考えるため、電圧を基準のベクトルに考えます。

R-L並列回路

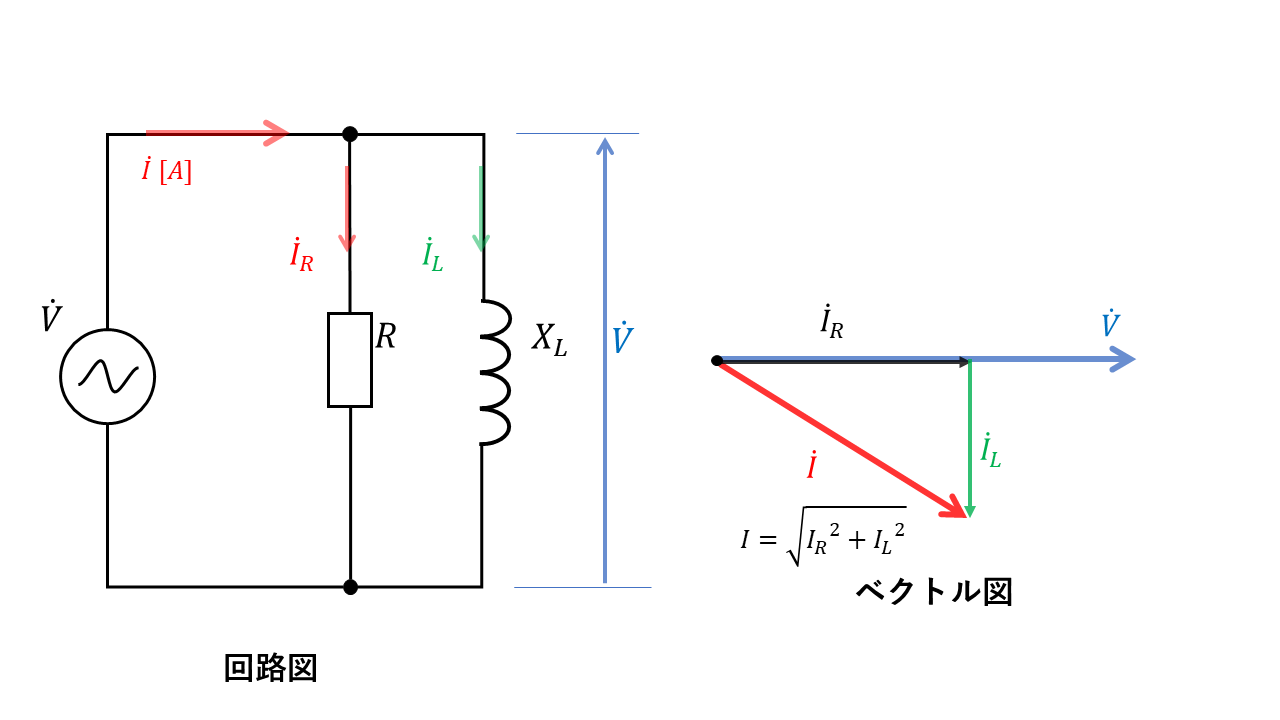
抵抗R、インダクタンスLを流れる電流の和は回路全体を流れる電流の大きさと同じになります。

$$\dot{I}=\dot{I_R} + \dot{I_L}$$

電源電圧Vの大きさ（\(dot{I}\)の長さ）は、ピタゴラスの定理より

$$ I = \sqrt{I_R^2 + I_L^2}$$

で求めることができる。

抵抗R、インダクタンスLにかかる電流の大きさは、[V]÷[Ω]で求めることができるので、

$$ I_R = \frac{V}{R} , I_L = \frac{V}{X_L}$$

となります。これを電流の式に代入して回路全体を流れる電流の大きさ\(I\)を求めます。

$$ \begin{align} I &= \sqrt{\left(\frac{V}{R}\right)^2 + \left(\frac{V}{X_L}\right)^2} \\ &=\sqrt{V^2\times {\left(\frac{1}{R}\right)^2 + \left(\frac{1}{X_L}\right)^2}} \\ &=V \sqrt{\left(\frac{1}{R}\right)^2 + \left(\frac{1}{X_L}\right)^2} \end{align} $$

以上のように計算することができます。

R-C並列回路

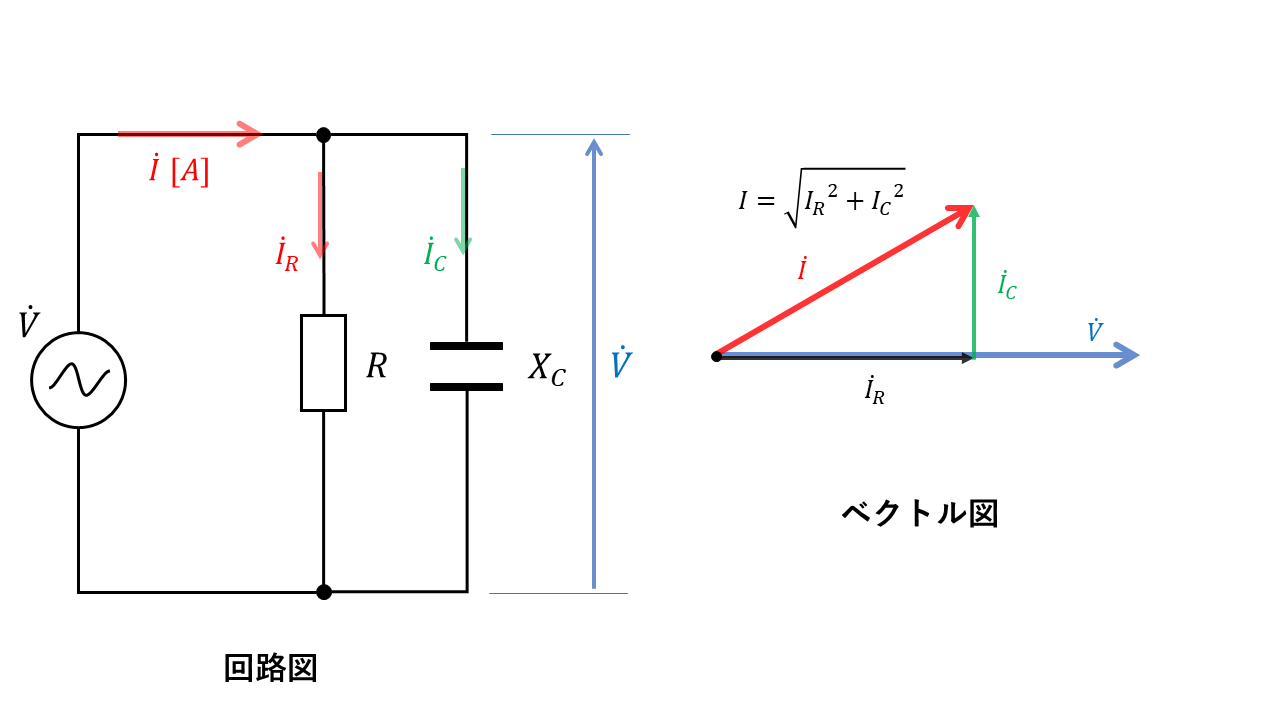
抵抗R、静電容量Cを流れる電流の和は回路全体を流れる電流の大きさと同じになります。

$$\dot{I}=\dot{I_R} + \dot{I_C}$$

電源電圧Vの大きさ（\(dot{I}\)の長さ）は、ピタゴラスの定理より

$$ I = \sqrt{I_R^2 + I_C^2}$$

で求めることができる。

抵抗R、静電容量Cにかかる電流の大きさは、[V]÷[Ω]で求めることができるので、

$$ I_R = \frac{V}{R} , I_C = \frac{V}{X_C}$$

となります。これを電流の式に代入して回路全体を流れる電流の大きさ\(I\)を求めます。

$$ \begin{align} I &= \sqrt{\left(\frac{V}{R}\right)^2 + \left(\frac{V}{X_C}\right)^2} \\ &=\sqrt{V^2\times {\left(\frac{1}{R}\right)^2 + \left(\frac{1}{X_C}\right)^2}} \\ &=V \sqrt{\left(\frac{1}{R}\right)^2 + \left(\frac{1}{X_C}\right)^2} \end{align} $$

以上のように計算することができます。

R-L-C並列回路

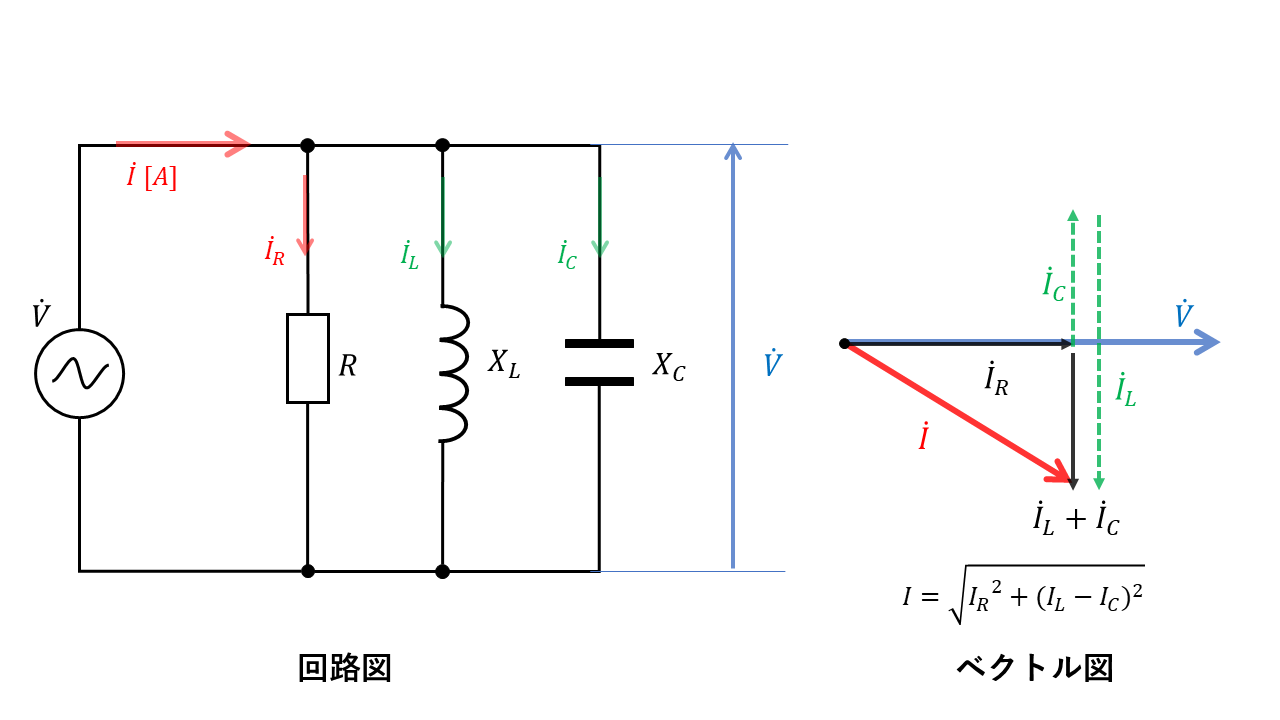
最後に、R-L-Cすべてが並列に接続された回路について解説します。

基本の計算方法はこれまでに紹介した回路と変わりませんが、インダクタンスLと静電容量Cは逆の働きをするという点に注意して計算を進めましょう。

$$\dot{I}=\dot{I_R} + \dot{I_L} + \dot{I_C}$$

ここで、\(\dot{I_L} + \dot{I_C}\)の絶対値は\(\vert I_L – I_C \vert \)とすること！！

回路全体の電流Iの大きさ（\(\dot{I}\)の絶対値）は、ピタゴラスの定理より

$$ \begin{align}I &= \sqrt{I_R^2 + (I_L – I_C)^2} \\ V &= \sqrt{\left(\frac{V}{R}\right)^2 + \left(\frac{V}{X_L} -\frac{V}{X_C}\right)^2} \\ &=\sqrt{V^2{\left(\frac{1}{R}\right)^2 + \left(\frac{1}{X_L} – \frac{1}{X_C}\right)^2}} \\ &=V \sqrt{\left(\frac{1}{R}\right)^2+\left( \frac{1}{X_L} – \frac{1}{X_C}\right)^2} \end{align} $$

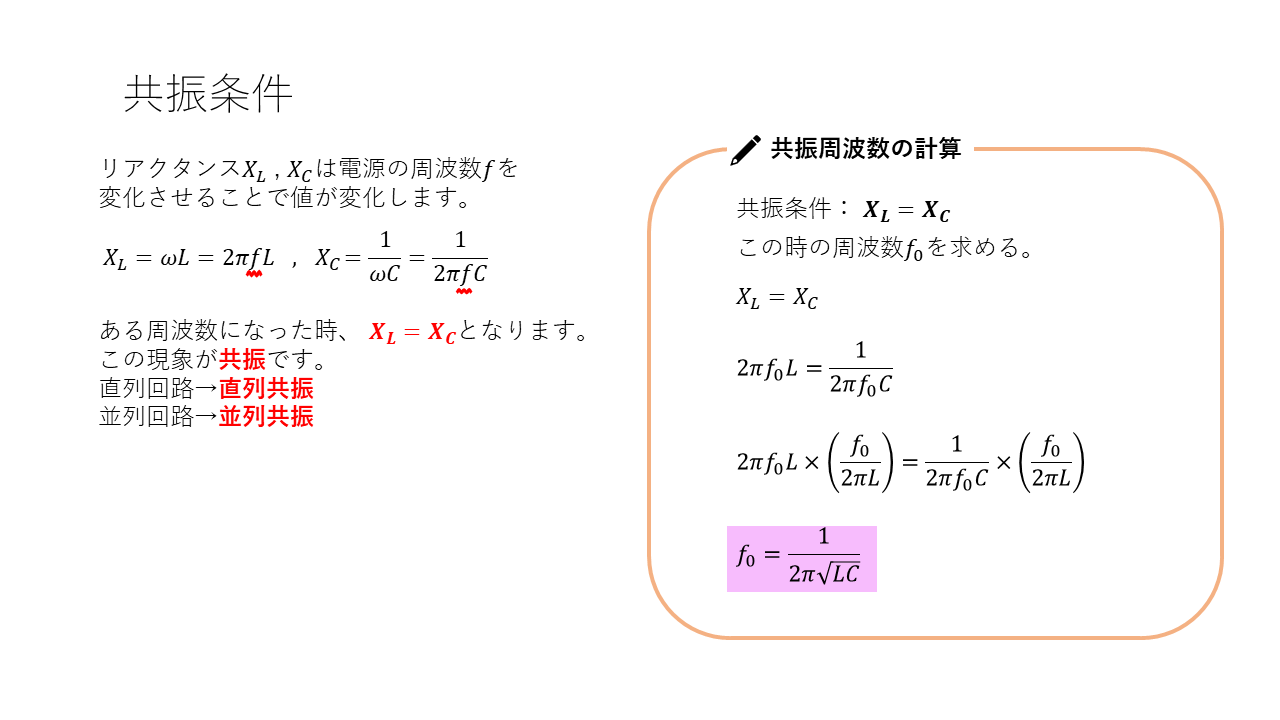
共振状態

R-L-C直列回路で電源の周波数\(f\)を変化させると、\(X_L , X_C\)[Ω]の値が変化します。

ある周波数\(f_0\)になった時、\( X_L = X_C \)となります。

この時の周波数\(f_0\)を共振周波数といい、電圧と電流が同位相となります。

R-L-C直列回路での共振

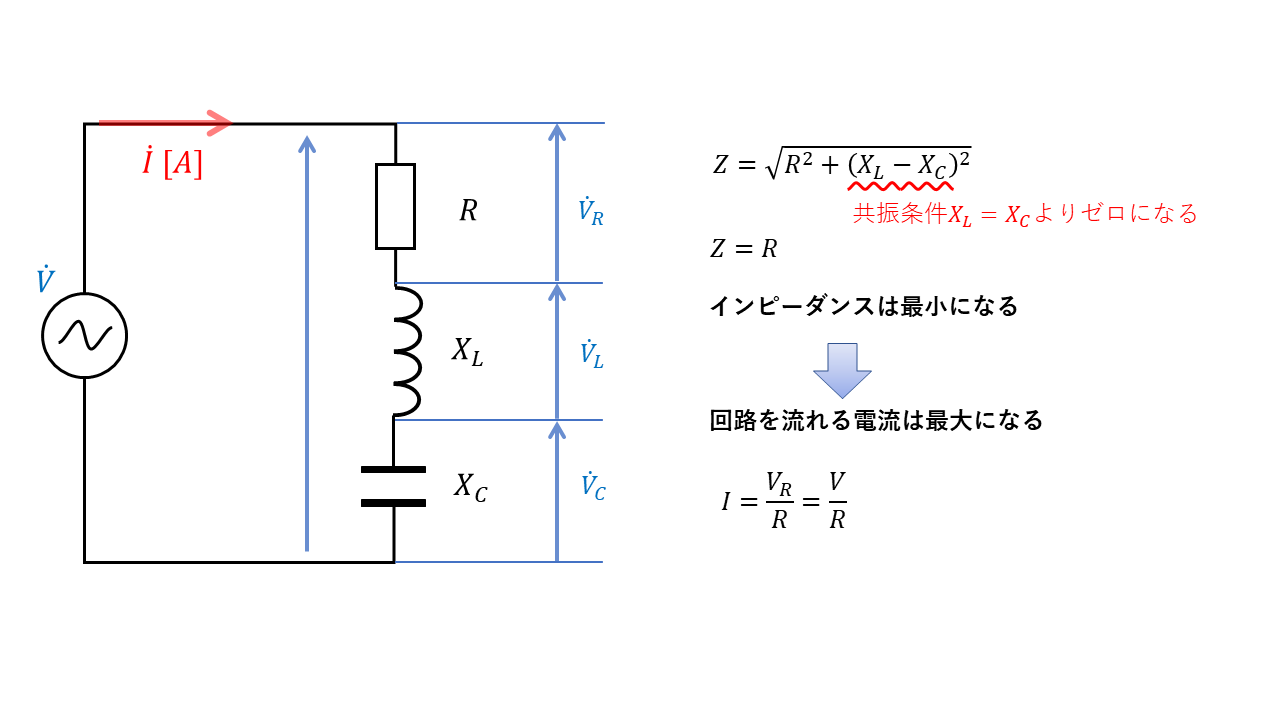
R-L-C直列回路において、共振状態となると

$$ Z = \sqrt{R^2 – ( X_L – X_C)^2} $$

の\(X_L – X_C = 0\)となり、インピーダンスが最も小さくなります。すなわち、回路を流れる電流が最大になります。

R-L-C並列回路での共振

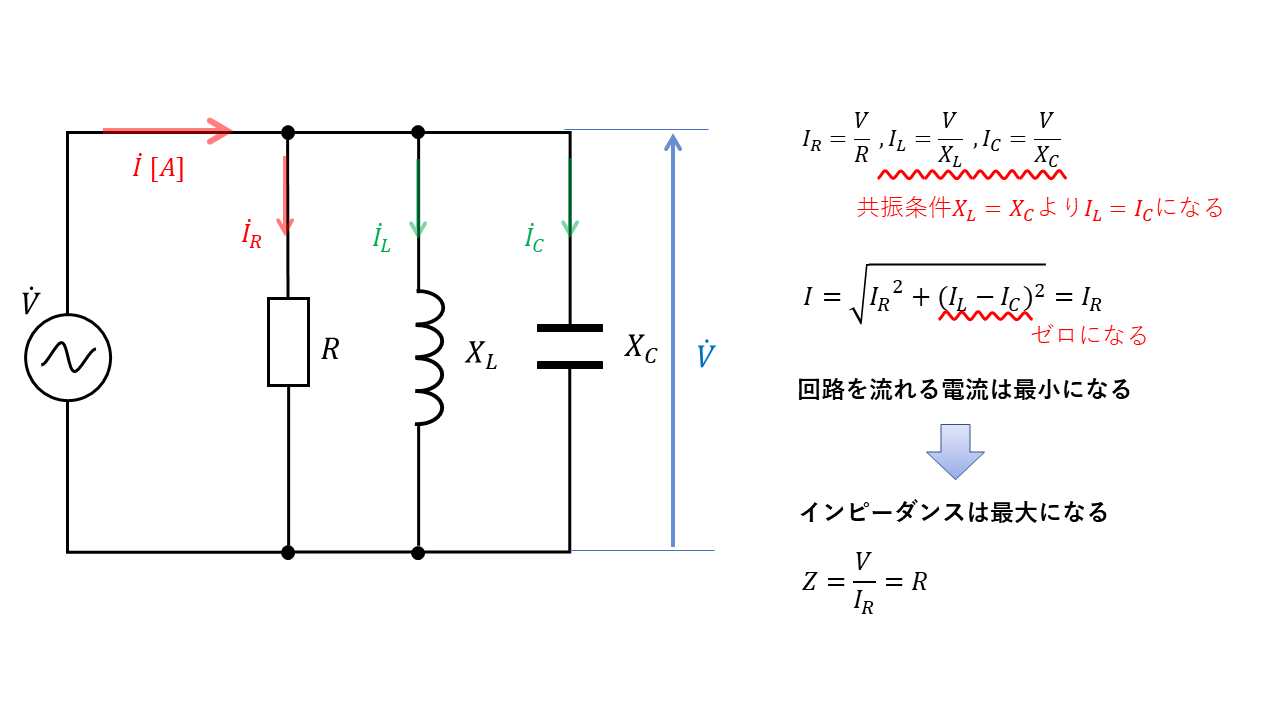
R-L-C並列回路では、共振状態になると

\(X_L = X_C\)より、

$$ \begin{align} \displaystyle \frac{V}{X_L} &= \frac{V}{X_C} \\ I_L &= I_C \end{align} $$

となり、回路に流れる電流が最小になます。すなわち、回路全体のインピーダンスが最大になり、インダクタンスLと静電容量Cが接続されていない時と同じ大きさの電流が流れる状態にあります。

まとめ