【解説】交流回路の電力計算

交流電力とは

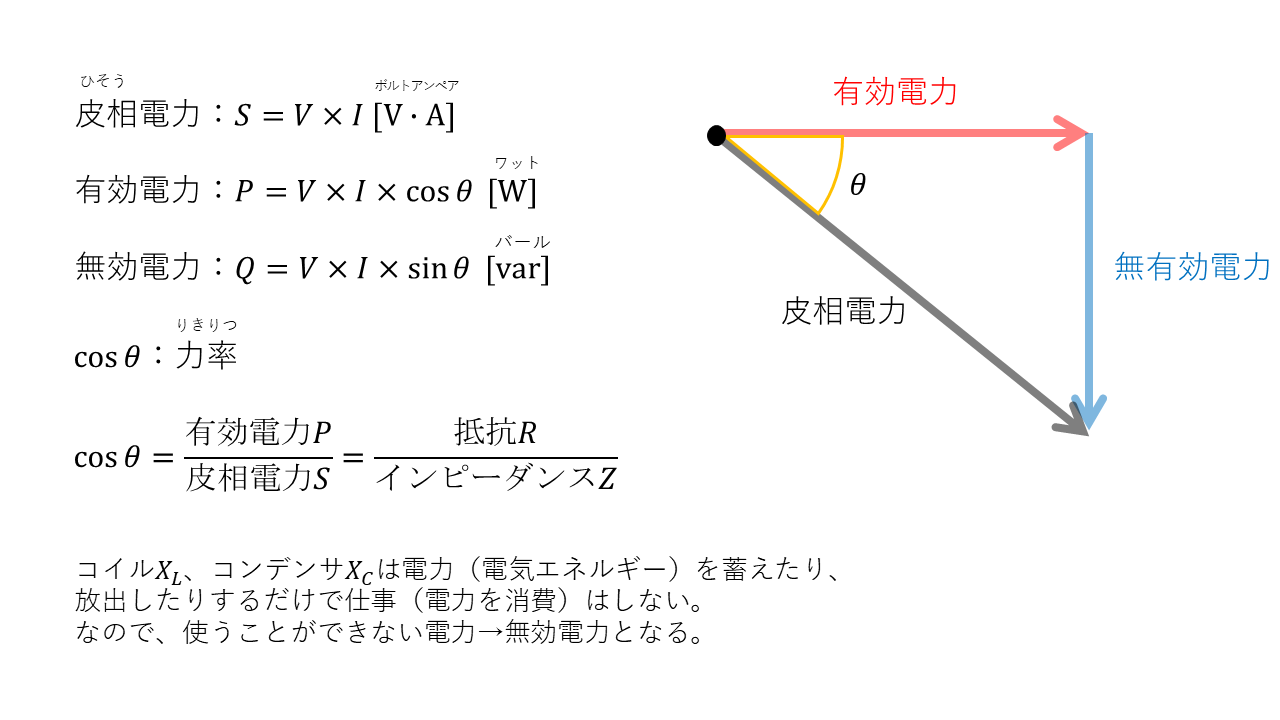
交流回路でも電力は、電圧V × 電流I で求めることができますが、交流では電圧・電流が絶えず変化しているため、電圧V × 電流I で計算できる電力は見かけ上の電力で皮相電力（記号：S、単位：V・A）と呼びます。

しかし、皮相電力にはコイルやコンデンサの充電・放電の特性による実際の仕事に利用できない電力も含まれています。この電力のことを無効電力（記号：Q、単位：var）と呼んでいます。

一方で、熱や運動エネルギーとして仕事に利用できる電力を有効電力（記号：P、単位：W）と呼びます。有効電力は、瞬時電力の1周期を平均した電力のことを指します。これは、交流電力が絶えす変化し扱いにくいためです。

※瞬時電力とは、交流回路のある瞬間における電力のこと

皮相電力の求め方

皮相電力は交流回路における見かけ上の電力を表すため、直流回路の時と同様に電圧×電流で求めることができます。

有効電力の求め方

有効電力とは電気エネルギーが熱や運動（仕事）に変換されて有効利用された電力のことを指します。そのため、消費電力と呼ばれることもあります。

抵抗Rのみの電力

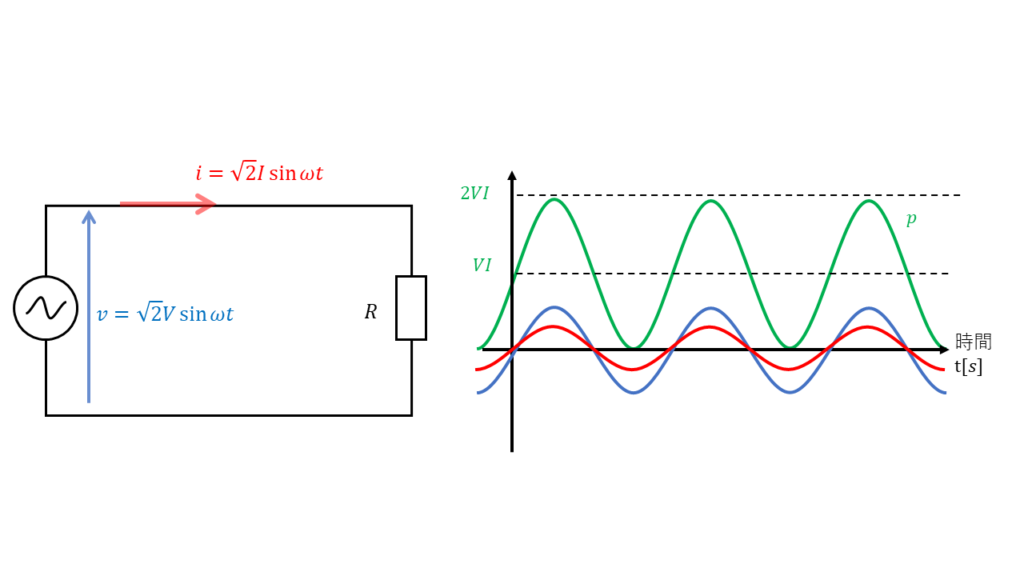
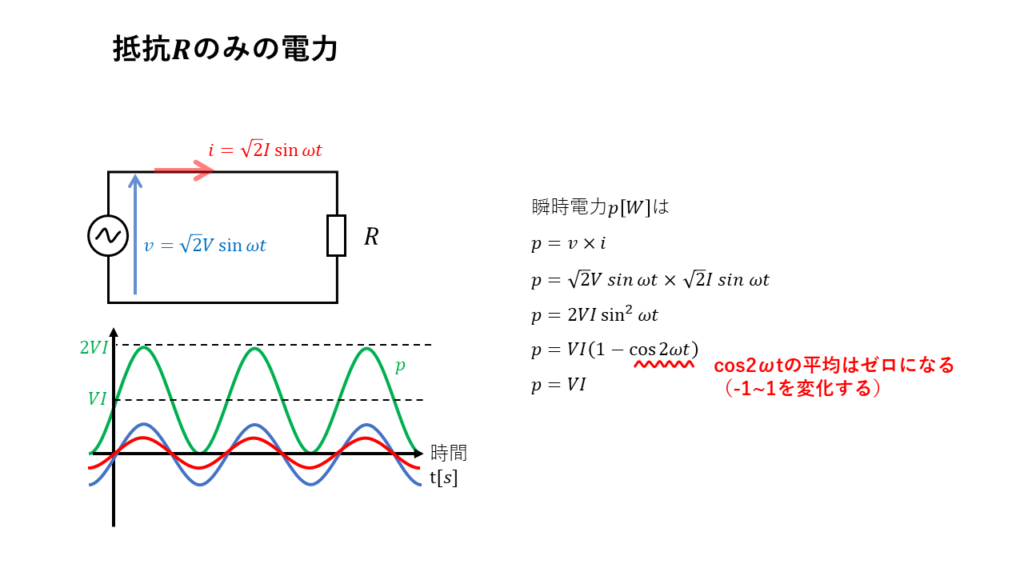
抵抗R[Ω]のみの回路に、交流電圧\( v = \sqrt{2}V\sin \omega t \) を加えたとき、

瞬時電力\(p\)[W] は \( p = v \times i\) なので、

\(\begin{align} p &= \sqrt{2} V \sin \omega t \times \sqrt{2} I \sin \omega t \\ &=2VI \sin^2 \omega t \end{align} \)

ここで2倍角の公式

\( \begin{align} \cos 2\theta &= 1 – 2\sin ^2 \theta \\ \Rightarrow 2\sin ^2 \theta &= 1 – \cos 2\theta \end{align} \)

を利用して、

\( \begin{align} p &= 2VI\sin ^2 \omega t \\ &= VI \times 2 \sin ^2 \omega t \\ &= VI \times \left( 1 – 2 \cos 2 \omega t \right) \\ &= VI – VI \cos 2 \omega t \end{align} \)

\(\cos 2 \omega t\)は-1～1の間を周期的に変化するので平均すると0になる。

よって、抵抗Rのみの有効電力は、

\( \begin{align} P &= 瞬時電力pの平均 \\ &= VI \end{align} \)

となります。

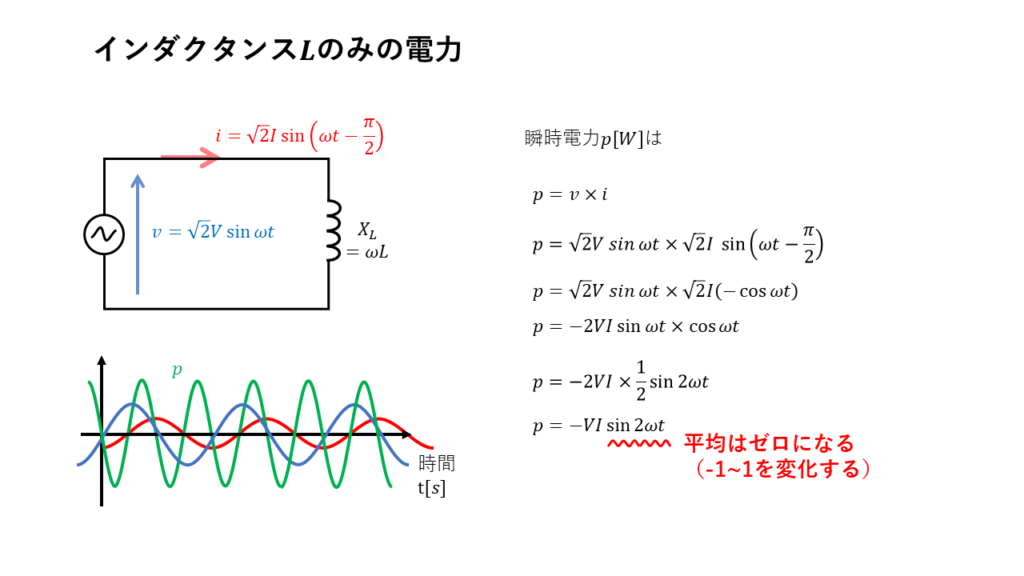
インダクタンスLのみの電力

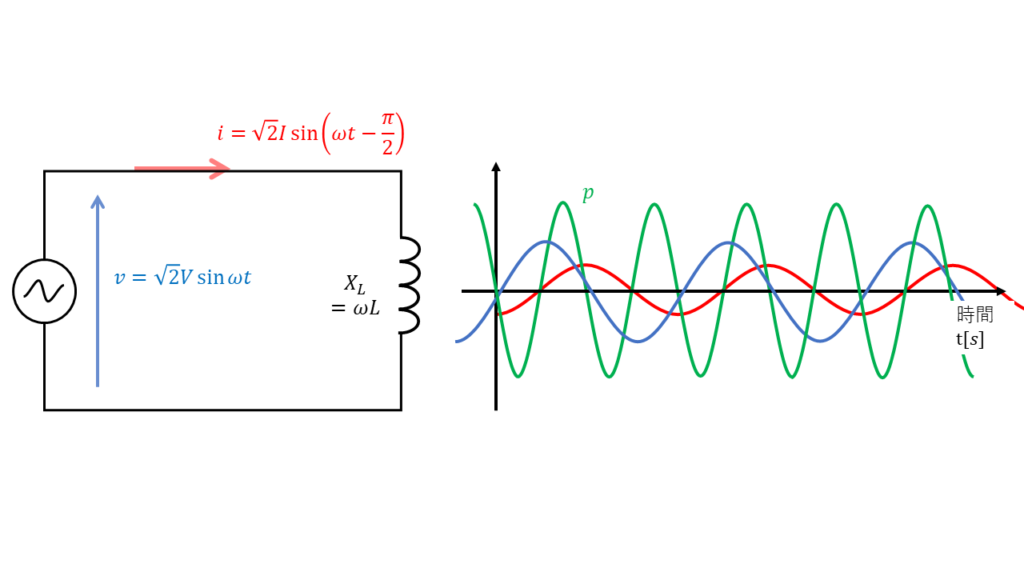
インダクタンスL[H]だけの回路に交流電圧\( v = \sqrt{2} V \sin \omega t\)を加えたとき、

遅れ電流\( i = \sqrt{2} I \sin \left( \omega t – \displaystyle \frac{\pi}{2} \right) \)が流れた場合について考える。

瞬時電力\(p\)[W] は \( p = v \times i\) なので、

\( \begin{align} p &= \sqrt{2} V \sin \omega t \times \sqrt{2} I \sin \left( \omega t – \displaystyle \frac{\pi}{2} \right) \\ &= \sqrt{2}V \sin \omega t \times \sqrt{2}I \times \left(- \cos \omega t \right) \\ &= -2VI \times \sin \omega t \times \cos \omega t \end{align} \)

ここで2倍角の公式

\( \begin{align} \sin 2\theta &= 2\sin\theta \times \cos \theta \\ \Rightarrow \sin\theta \times \cos\theta &= \displaystyle \frac{1}{2} \sin2\theta \end{align} \)

を利用して、

\( \displaystyle \begin{align} p &= -2VI \sin\omega t \times \cos \omega t \\ &= -2VI \times \frac{1}{2} \sin 2 \omega t \\ &= -VI \sin 2 \omega t \end{align} \)

\(\sin 2\omega t\)は-1~1の間を周期的に変化するだけなので、平均した値は0となる。

よってインダクタンスLのみの場合の有効電力は、

\( \begin{align} P &= 瞬時電力pの平均 \\ &= -VI \sin 2 \omega t の平均値 \\ &= 0 \end{align} \)

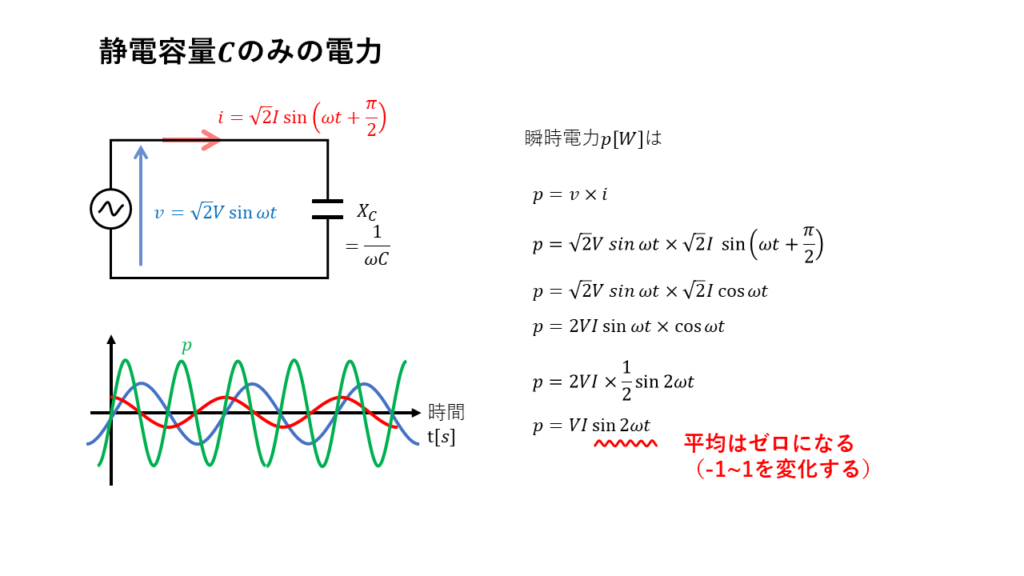
静電容量Cのみの電力

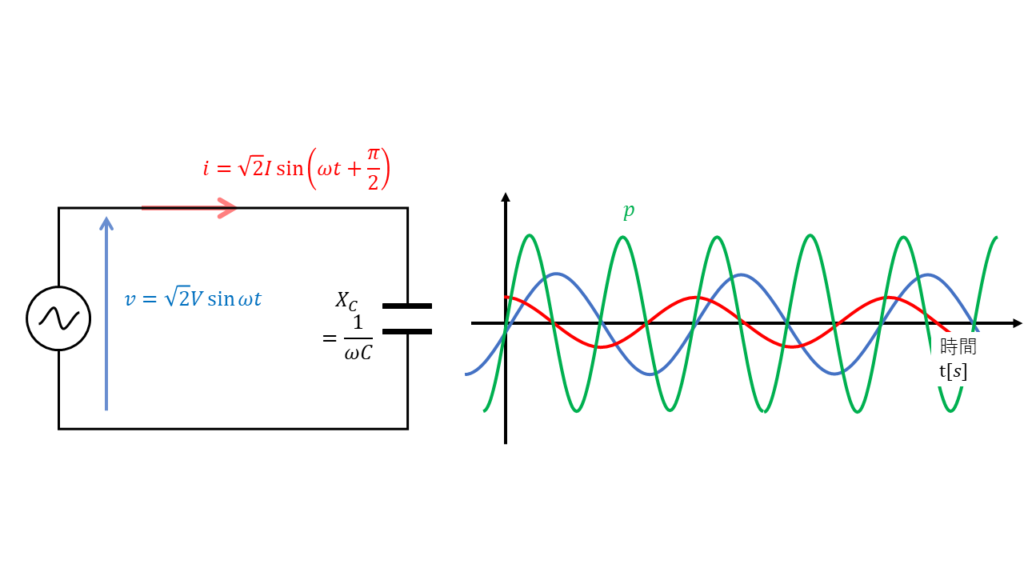
静電容量C[F]だけの回路に交流電圧\( v = \sqrt{2} V \sin \omega t\)を加えたとき、

遅れ電流\( i = \sqrt{2} I \sin \left( \omega t + \displaystyle \frac{\pi}{2} \right) \)が流れた場合について考える。

瞬時電力\(p\)[W] は \( p = v \times i\) なので、

\( \begin{align} p &= \sqrt{2} V \sin \omega t \times \sqrt{2} I \sin \left( \omega t + \displaystyle \frac{\pi}{2} \right) \\ &= \sqrt{2}V \sin \omega t \times \sqrt{2}I \times \left( \cos \omega t \right) \\ &= 2VI \times \sin \omega t \times \cos \omega t \end{align} \)

ここで2倍角の公式

\( \begin{align} \sin 2\theta &= 2\sin\theta \times \cos \theta \\ \Rightarrow \sin\theta \times \cos\theta &= \displaystyle \frac{1}{2} \sin2\theta \end{align} \)

を利用して、

\( \displaystyle \begin{align} p &= 2VI \sin\omega t \times \cos \omega t \\ &= 2VI \times \frac{1}{2} \sin 2 \omega t \\ &= VI \sin 2 \omega t \end{align} \)

\(\sin 2\omega t\)は-1~1の間を周期的に変化するだけなので、平均した値は0となる。

よって静電容量Cのみの場合の有効電力は、

\( \begin{align} P &= 瞬時電力pの平均 \\ &= -VI \sin 2 \omega t の平均値 \\ &= 0 \end{align} \)

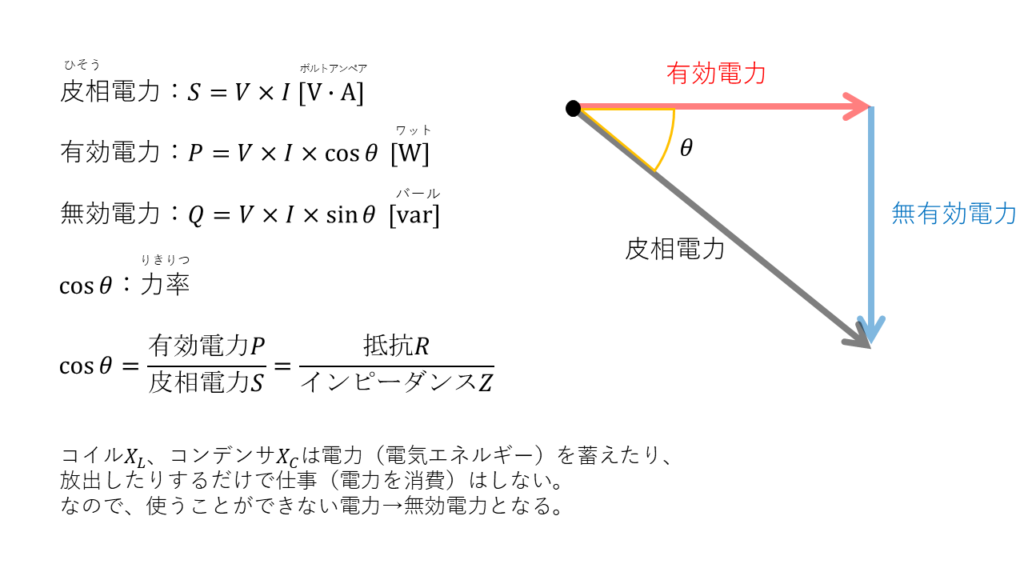
力率とは

電圧V × 電流I で求めることができる見かけ上の電力（皮相電力）のうち、有効電力 \( P = V \times I \times \cos \phi\) として働いた割合のことを力率 \(\cos \phi\) と呼びます。

無効電力の求め方

交流回路の見かけ上の電力（皮相電力）のうち熱や運動エネルギーとして取り出すことができなかった分（コイルやコンデンサに蓄えられただけで送り返されてしまった電力）を無効電力と呼びます。

別の言い方をすると、コイルやコンデンサが充電・放電するための電力のことを無効電力ということもできます。

無効電力は電源からコイル・コンデンサ間の電線を移動するため、電線の許容電流には影響を与えますが仕事をすることはありません。

まとめ