電界とは｜電気力線と電束の違い

電験三種　理論科目の問1、2の静電気の範囲では必ずと言っていいほど、コンデンサの電界に関する問題が出題されます。今回は、電界を考える基礎となる電気力線や電束について解説していきます。

電界とは

電荷（電気を帯びた粒）の周囲には、静電気の力が働く空間が存在します。この空間を電界と呼びます。

電界は目で見ることができないため、上図のように矢印を使って表します。この電界を表す矢印を「電気力線」と呼びます。

電界…静電気の力（電荷が引っ張られたり、押されたりする）空間のことを電界と呼びます。
記号：\( E \)　、　単位：\( \rm [\ V/m \ ] \)

電界中で1 [C]あたりの電荷にはたらく静電気力の大きさをと向きを電界の強さといいます。

電界の大きさ

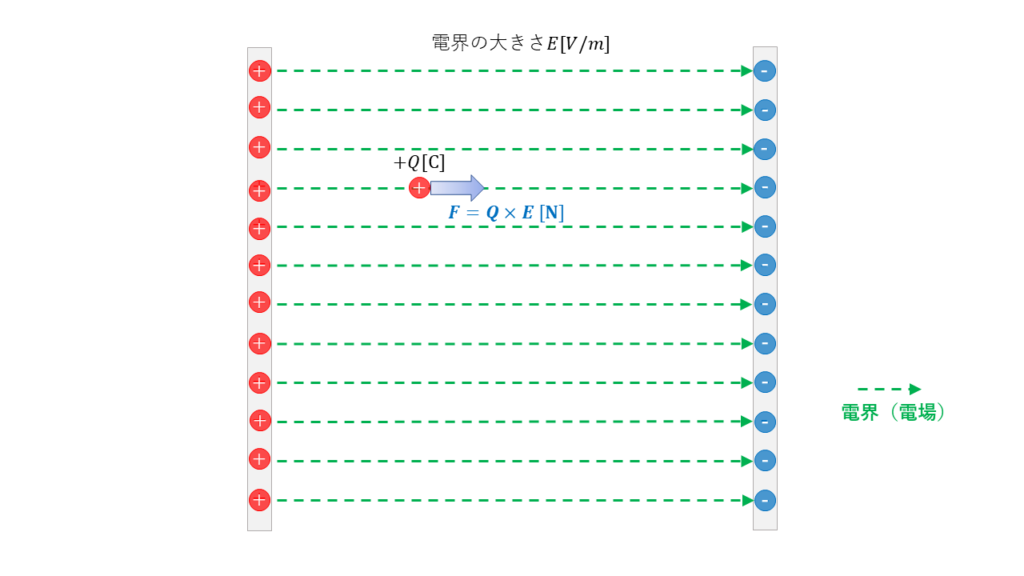
電界\(E\)[V/m]中に\(+Q\)[C]の電荷を置いた時に、電荷に働く静電気力の大きさ\(F\)[N]は、

\( \begin{align} F &= Q \times E \\ \\ 静電気力\rm [N] &= 電荷 \rm [C] \times 電界の大きさ \rm [V/m] \end{align} \)

と表せます。
また、クーロンの法則より\(+Q\)[C]の電荷に働く力\(F\)[N]は、

\( \begin{align} F &= \displaystyle \frac{ Q_1 \times Q }{ 4 \pi ε r^2 } \tag{1} \\ \\ F &= Q \times E \tag{2} \end{align} \)

この2つの式を比べると、電界\(E\)[V/m]の大きさは

\( E = \displaystyle \frac{Q_1}{4 \pi ε r^2} \)

と表すことができます。
したがって、電界の大きさを電荷\(Q\)、誘電率\( ε \)、距離\( r \)を使って、

\( E = \displaystyle \frac{Q}{ 4 \pi ε r^2 } \)

となります。

電気力線のルール

電界は目で見ることができないため、仮想の線で電界の様子を可視化したものを電気力線と呼びます。

電気力線ルール①

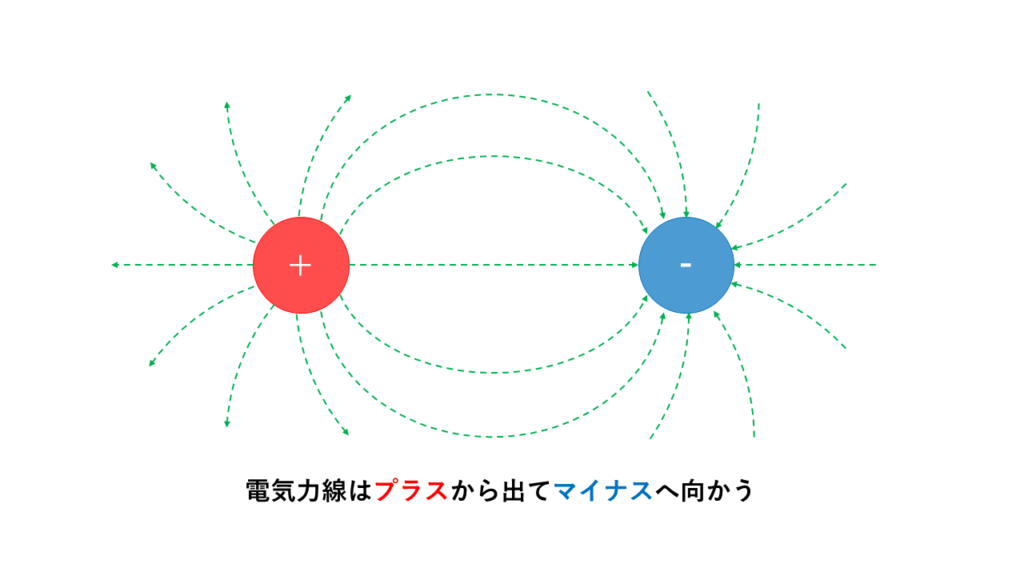
電気力線は正電荷から出て、負電荷に吸い込まれる。

点電荷から出てくる電気力線の本数は、\(\displaystyle \frac{Q}{ε}\)[本]である。

電気力線ルール②

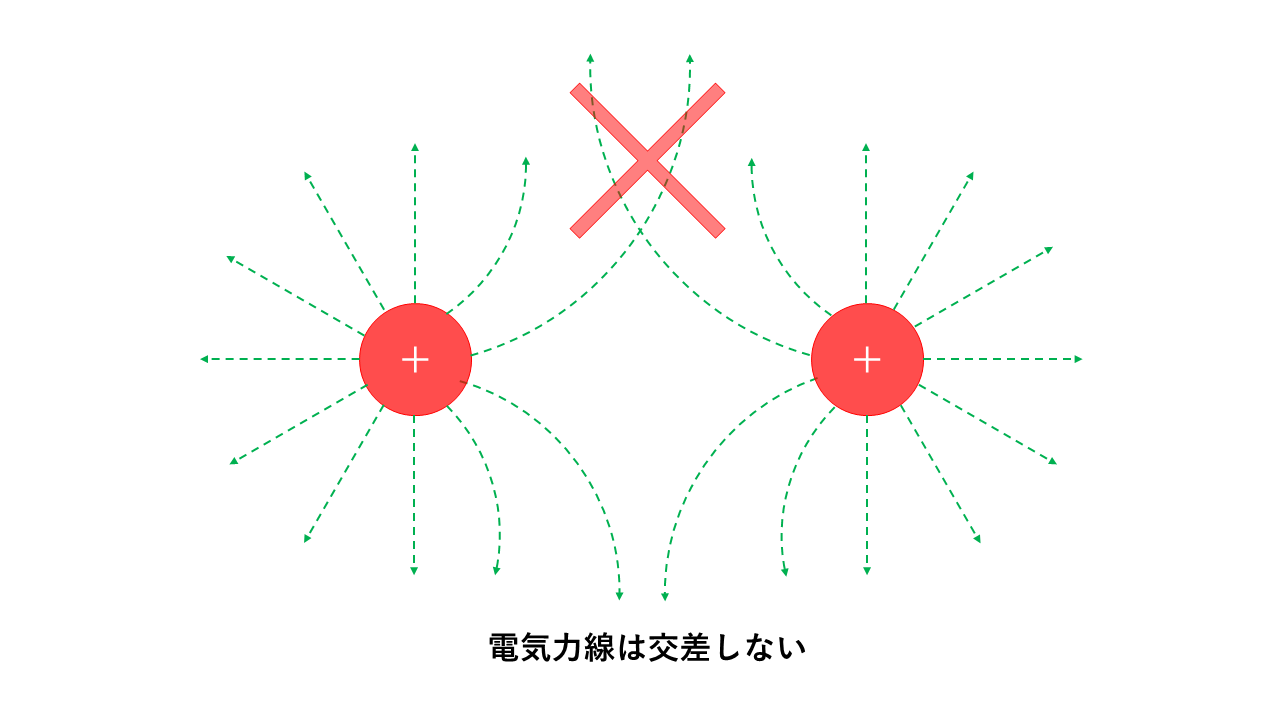
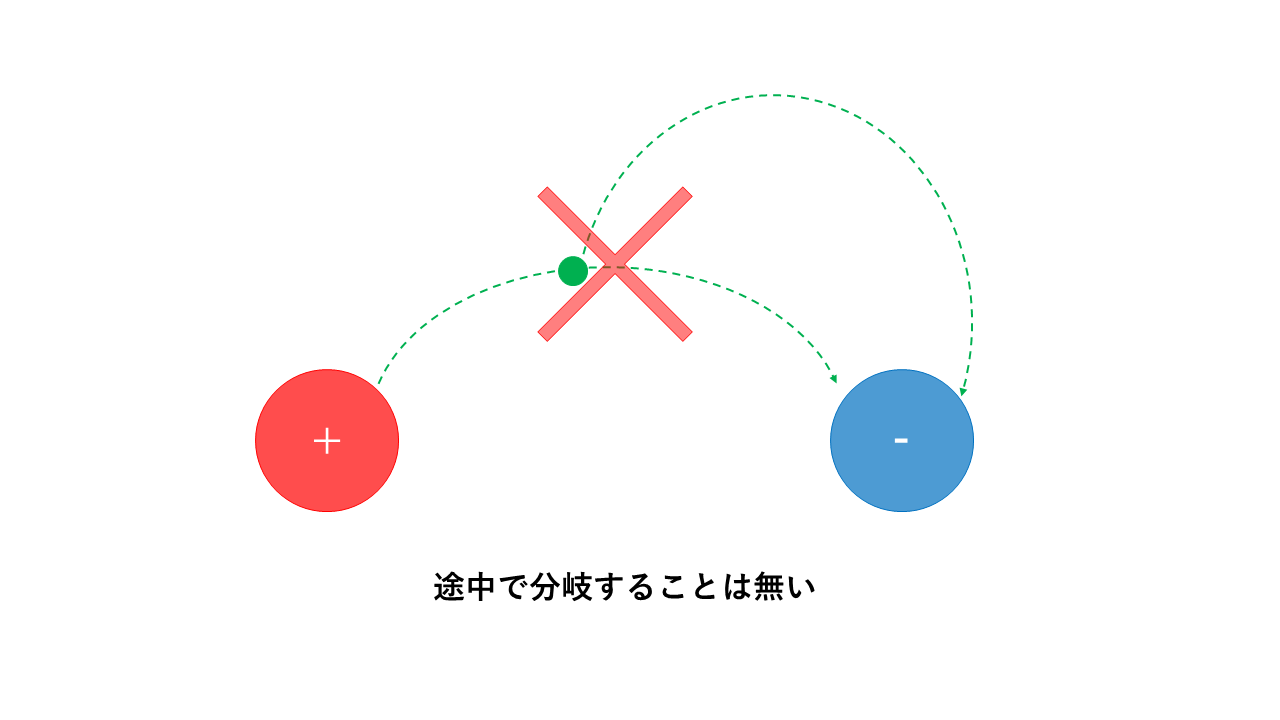
電気力線同士が交差することは無い。また、電気力線が途中で分岐したり、消えたりしない。

電気力線ルール③

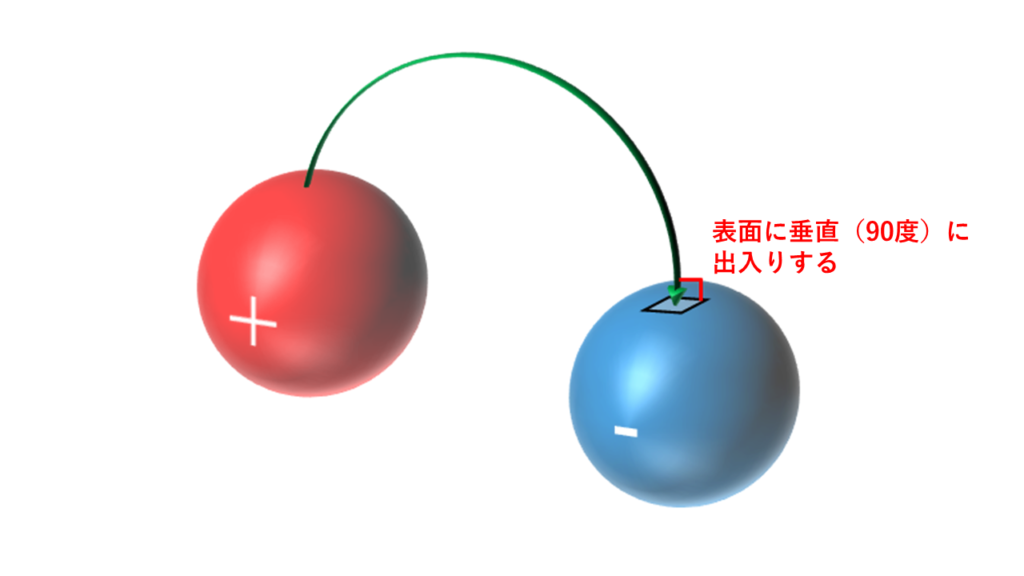
電気力線は導体の表面に垂直に出入りし、導体内部には存在しない。

電気力線ルール④

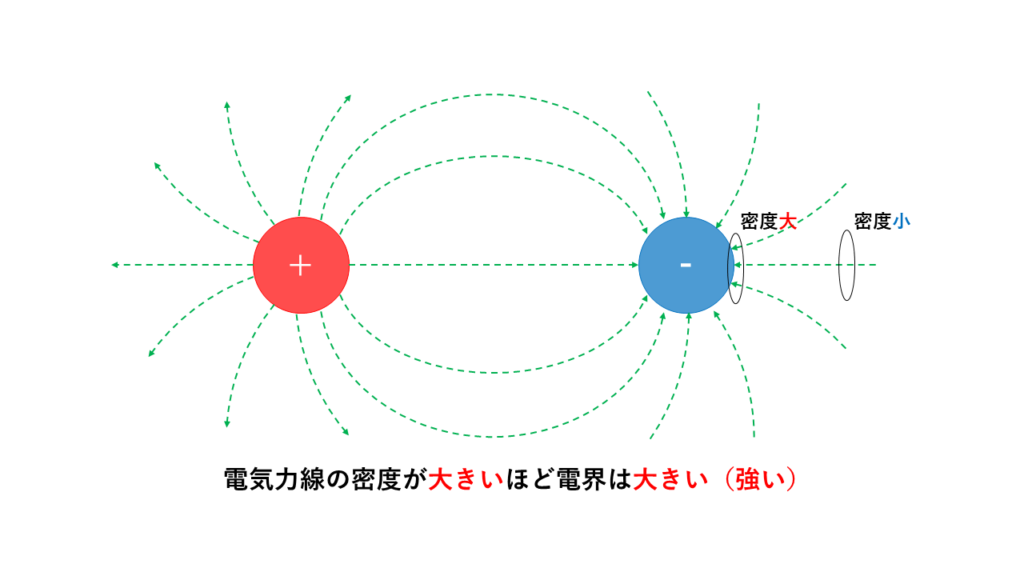
電気力線の接線の向きと、その伝の電界の向きは一致する。電気力線の\(1\)[\(m^2\)]あたりの密度は、その点の電界の大きさを表す。

点電荷の電気力線

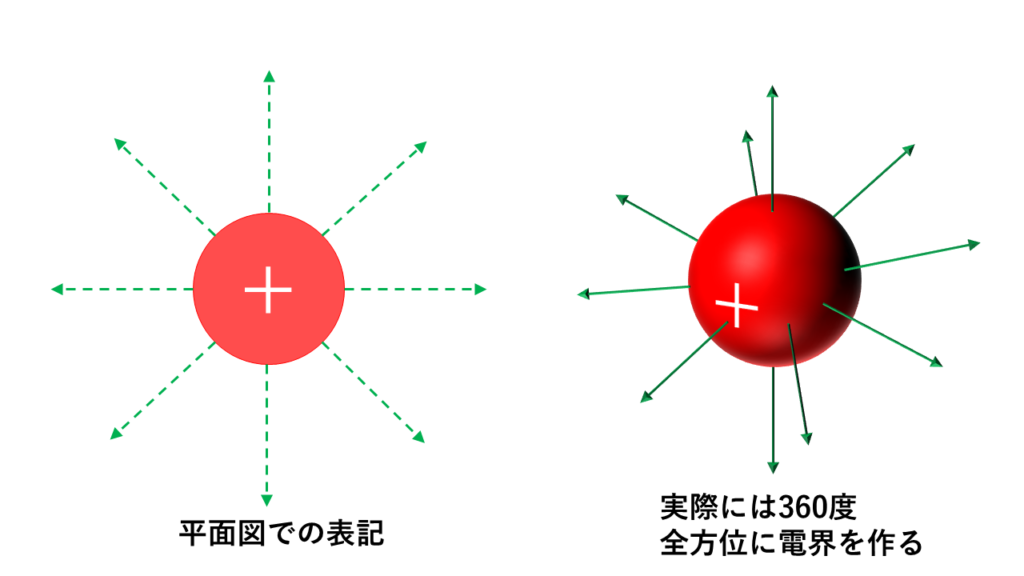
点電荷からは、全方位に電気力線が湧き出ています。

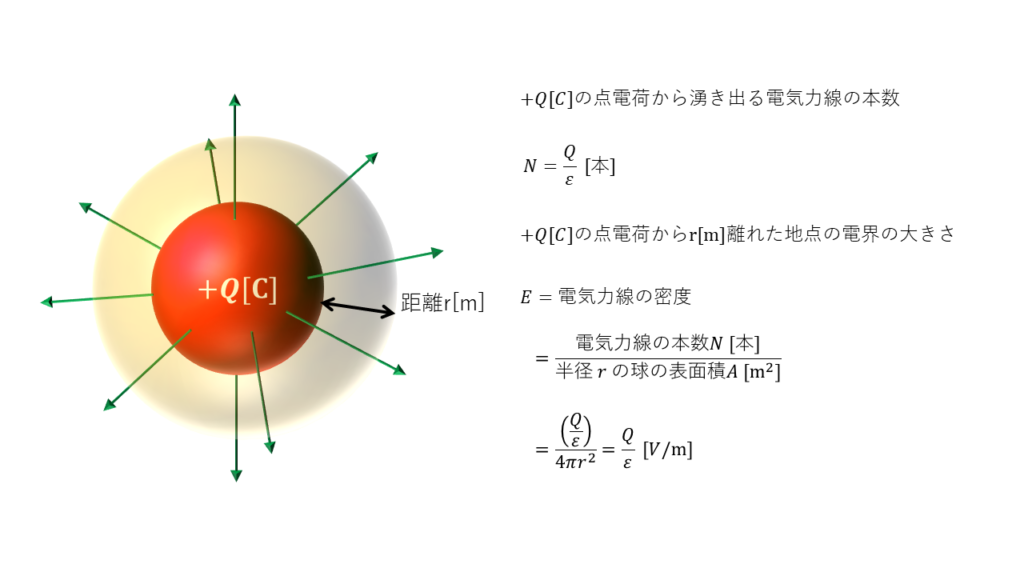
\(+Q\)[C]の点電荷から湧き出る電気力線の本数\(N\)は誘電率\(ε\)[F/m]とすると、

\( N =　\displaystyle \frac{Q}{ε} \)

また、\(+Q\)[C]の点電荷から\(r\)[m]離れた点の電界の大きさ\(E\)[V/m]は、

\( \begin{align} E &= \frac{電気力線の本数 N[本]}{半径rの級の表面積A[m^2]} \\ \\ &=\frac{\displaystyle \left(\frac{Q}{ε}\right) }{4\pi ε r^2} [V/m] \end{align} \)

となります。

2つの電荷が作る電界

2つの点電荷が直線状にあるとき

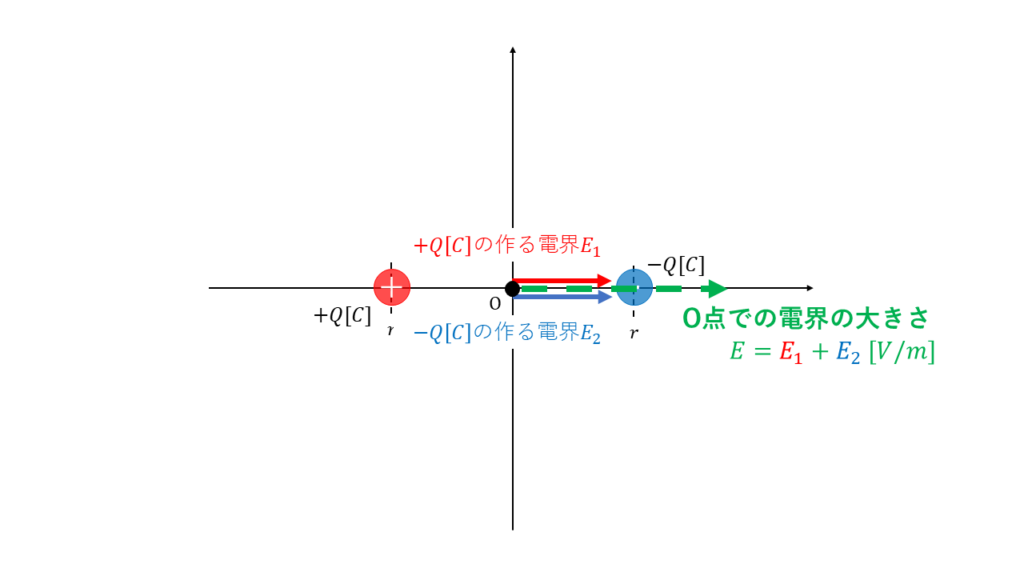
2つの点電荷が直線状にあるとき、電界は足し算で計算することができます。

+Q[C]が原点Oに作る電界\(E_1\)は、

\( E_1 = \displaystyle \frac{Q}{4\pi ε r^2} \tag{右向き} \)

また、-Q[C]が原点Oに作る電界\(E_2\)は、

\( E_2 = \displaystyle \frac{Q}{4\pi ε r^2} \tag{左向き} \)

したがって、原点Oに生じる電界の大きさ\(E\)[V/m]は、

\( \begin{align} E &= E_1 + E_2 \\ \\ &= \displaystyle \frac{Q}{4\pi ε r^2} + \displaystyle \frac{Q}{4\pi ε r^2} \\ \\ &= \displaystyle \frac{2Q}{4\pi ε r^2} = \displaystyle \frac{Q}{2\pi ε r^2} \end{align} \)

2つの電荷が直線状に無いとき

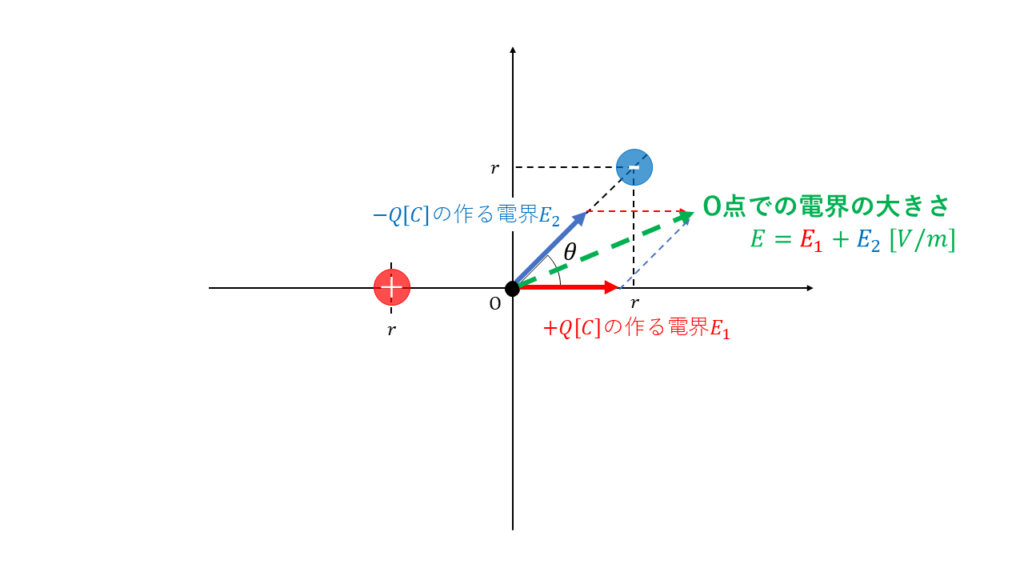
2つの電界が角度\(\theta\)で交わっているときの電界の大きさはベクトルの足し算になります。

+Q[C]の電荷が作る電界\(E_1\)

\( E_1 = \displaystyle \frac{Q}{4\pi ε r^2} \)

-Q[C]の電荷が作る電界\(E_2\)

\( E_2 = \displaystyle \frac{Q}{4\pi ε r^2} \)

ここで、電界\(E_2\)は横軸と角度\(\theta\)をなすので、横軸方向と縦軸方向のそれぞれに分解すると、次のようになります。

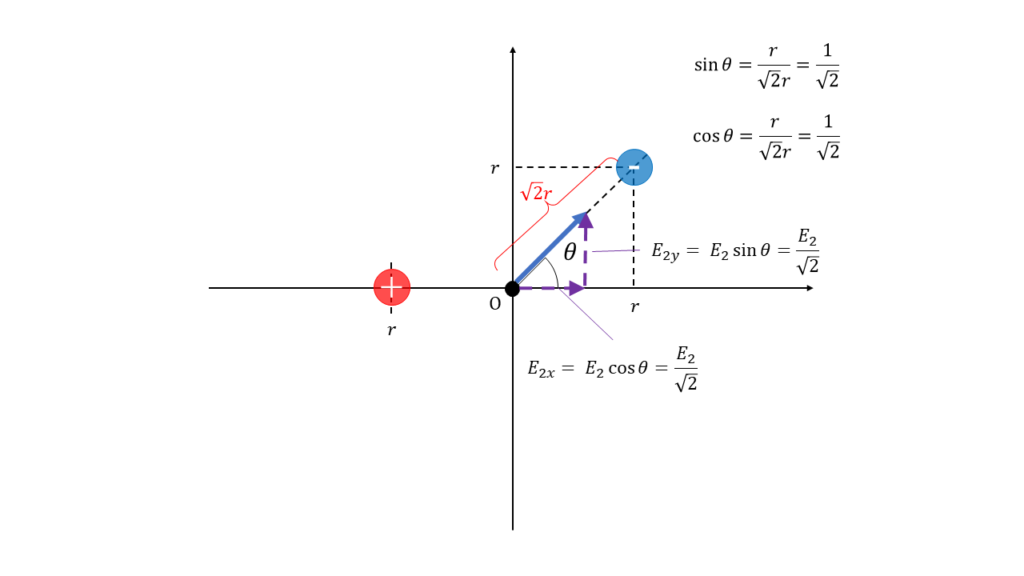
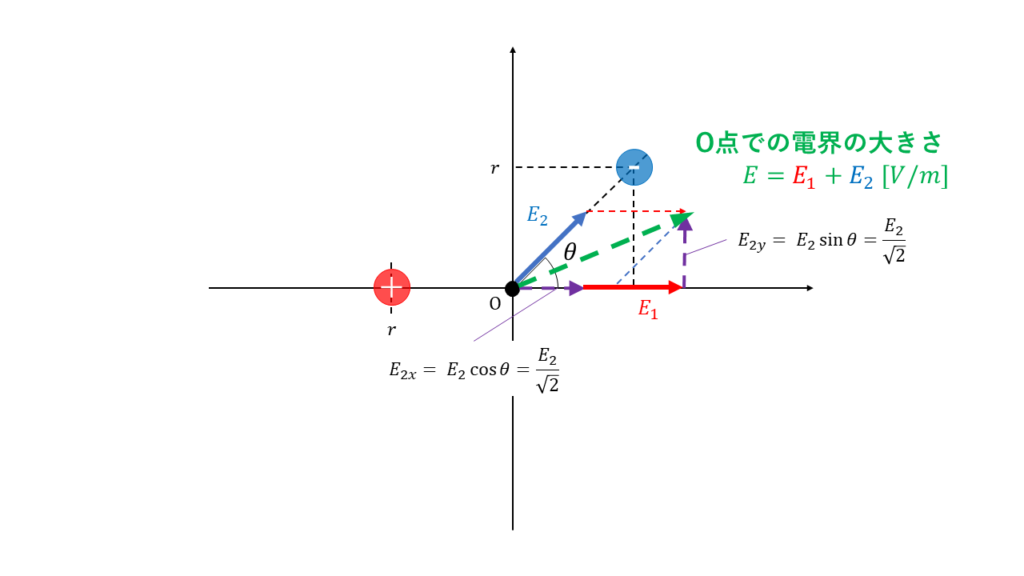
横軸方向、縦軸方向のベクトルをそれぞれ足し算します。

横軸方向\(E_x\)の電界の大きさ

\( \begin{align} E_x &= E_1 + E_{2x} \\ \\ &= \displaystyle \frac{Q}{4\pi ε r^2} + \displaystyle \frac{Q}{4\sqrt{2}\pi ε r^2} \\ \\ &= \displaystyle \frac{2Q}{8\pi ε r^2} + \displaystyle \frac{\sqrt{2}Q}{8\pi ε r^2} \\ \\ &= \displaystyle \frac{\left(2+\sqrt{2} \right) Q}{8\pi ε r^2} \end{align} \)

縦方向\(E_y\)の電界の大きさ

\( \begin{align} E_y &= E_{2y} \\ &= \displaystyle \frac{E_2}{\sqrt{2}} \\ \\ &= \displaystyle \frac{Q}{4\sqrt{2}\pi ε r^2} \\ \\ &= \displaystyle \frac{\sqrt{2}Q}{8\pi ε r^2} \end{align} \)

したがって、合計のベクトルの大きさ\(E\)はピタゴラスの定理より

\( \begin{align} E &= \sqrt{E_x^2 + E_y^2} \\ \\ &=\sqrt{\left( \displaystyle \frac{\left(2+\sqrt{2} \right) Q}{8\pi ε r^2} \right)^2 + \left( \displaystyle \frac{\sqrt{2}Q}{8\pi ε r^2} \right)^2} \\ \\ &= \displaystyle \frac{\sqrt{(8+2\sqrt{2})}Q}{8\pi ε r^2} \approx \displaystyle \frac{3.290Q}{8\pi ε r^2}\end{align} \)

静電遮へい

①導体内部の遮へい

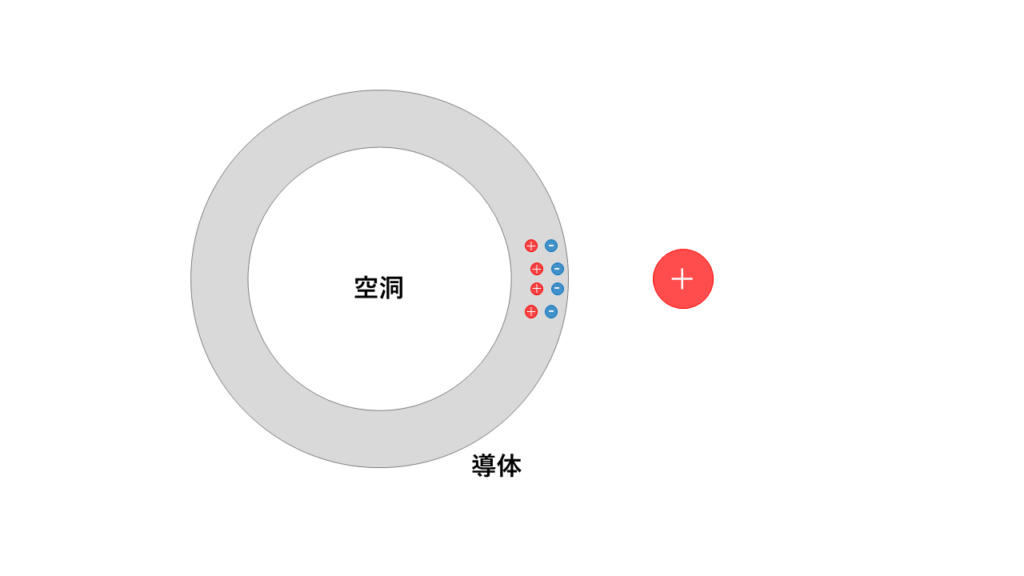
内部が空洞の導体に電荷をもった物体を近づけると、導体の中で電荷の移動が発生します。

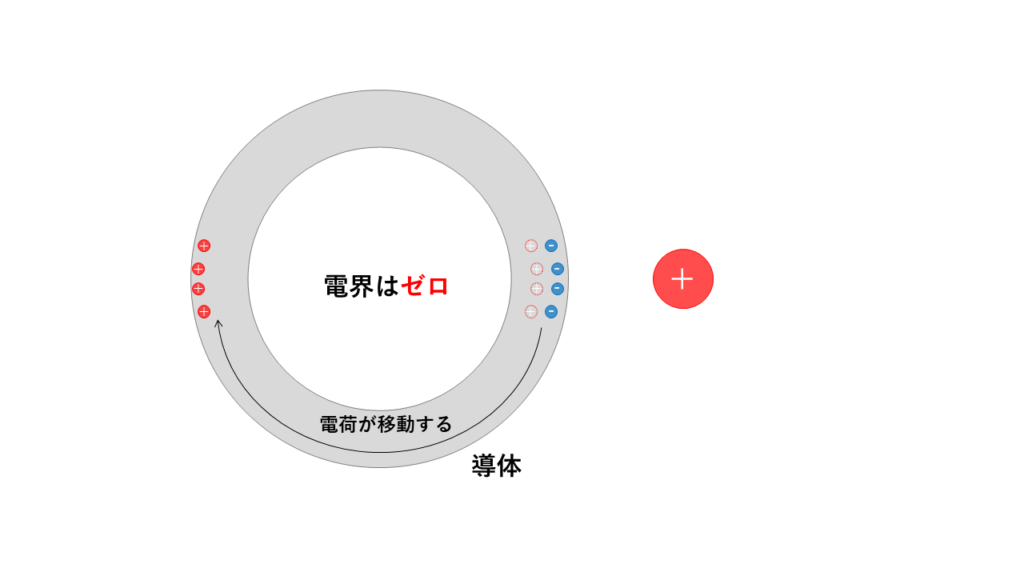
外部からの電界は導体内部の電荷の移動により打ち消されてしまうので、空洞部分には電界が発生しません。これを静電遮蔽と呼びます。

②導体内部の電界を外部に漏らさない遮へい

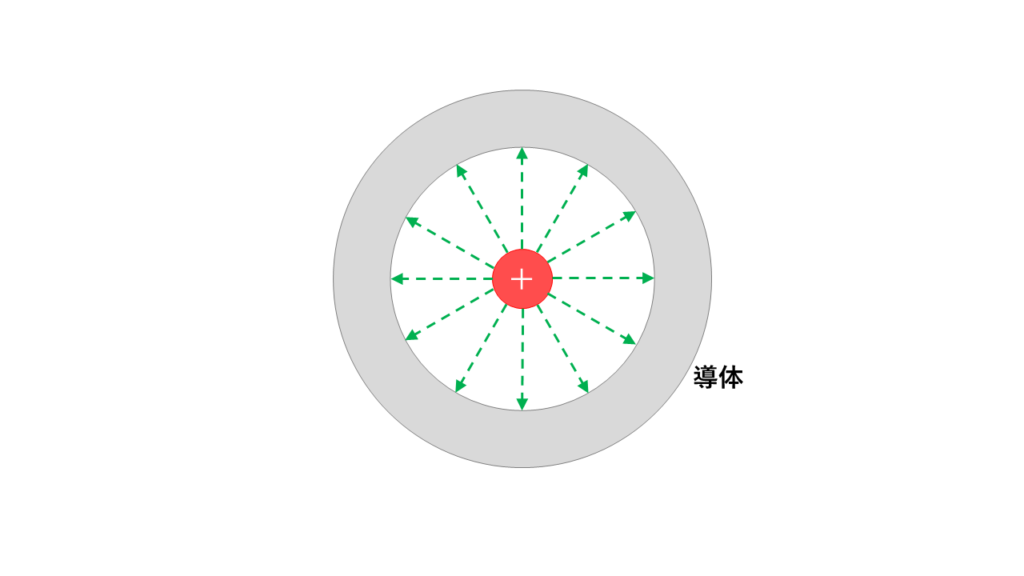
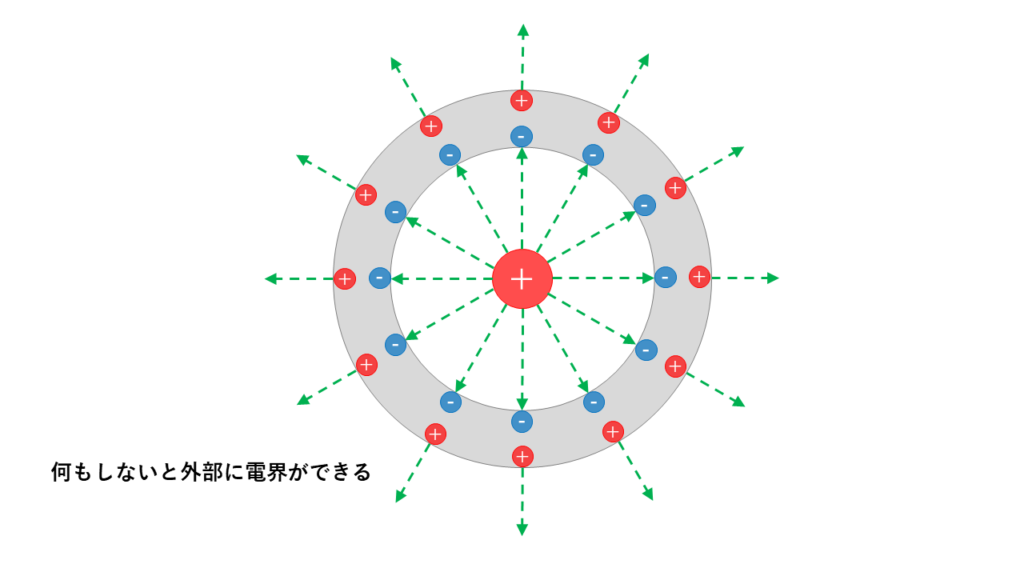
図のように導体の空洞部分に点電荷を置いた場合について考えます。通常の場合、導体内部の電荷の配列が整えられて、外部にも電界が発生してしまします。

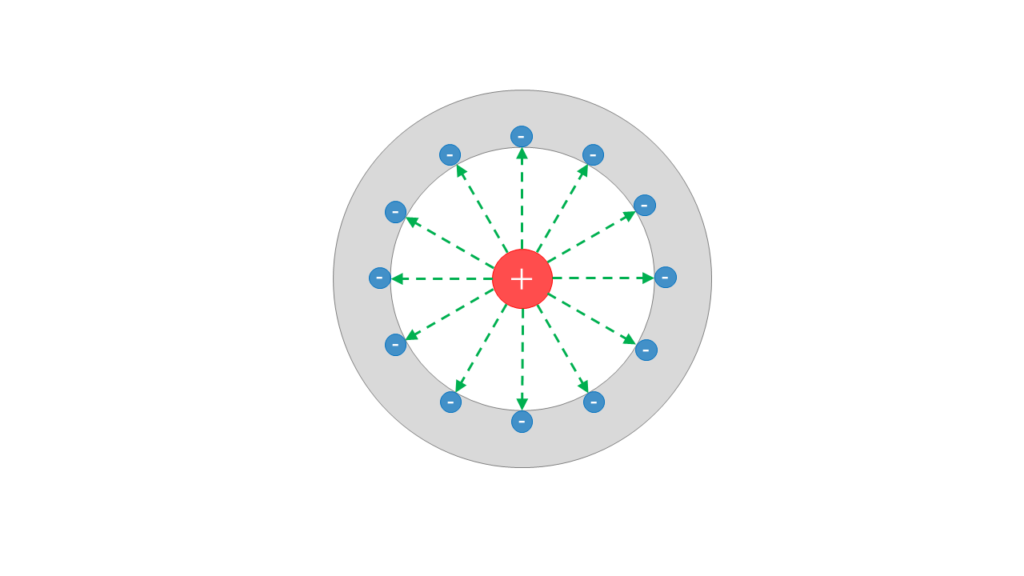
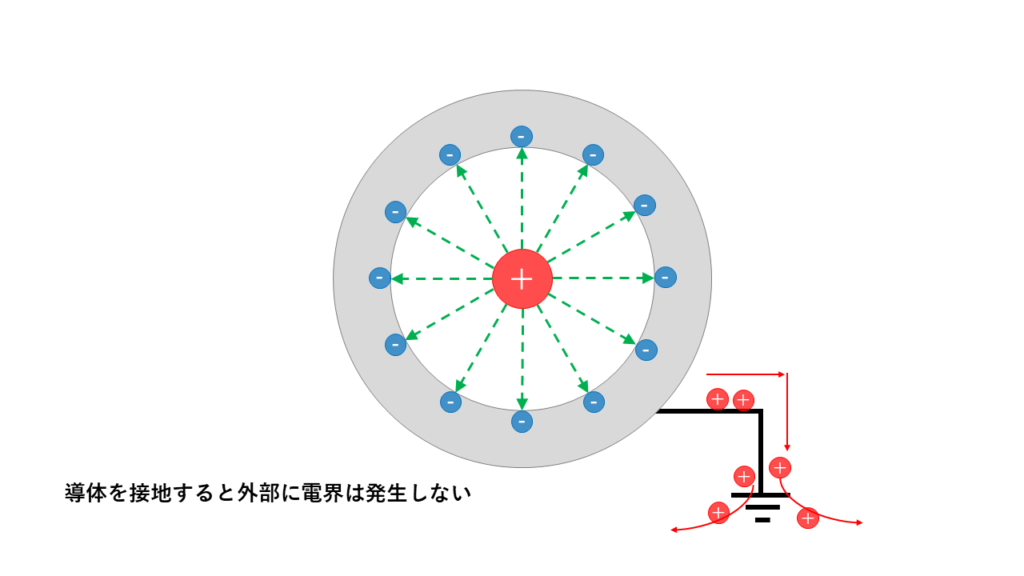
しかし、導体に接地を施した場合、電荷が接地線を通して地面へと逃げていくため外部に電界を発生させません。この状態も静電遮蔽といいます。

電束と電束密度

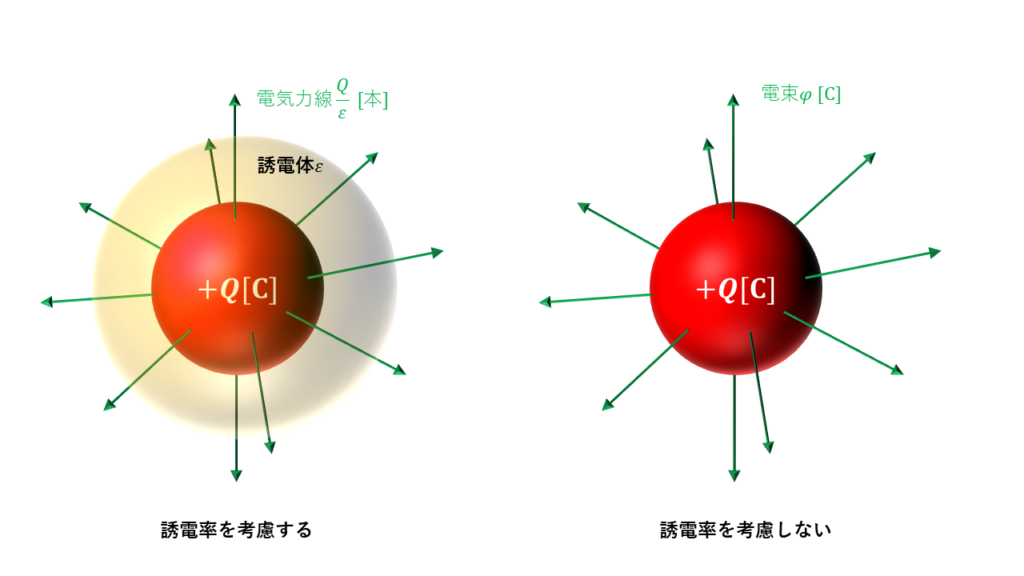
電気力線は周囲の誘電率に影響を受けるため、誘電率の異なるぶっりつが複数存在する場合の電界を考える場合に不便です。そこで、誘電率の影響を考えない電束という概念が生まれました。

電束と電気力線の主な違いは次の2点です。

• 周囲の誘電率を考慮しない
• 電荷から湧き出る線の数え方が違う
  電気力線\(\displaystyle \frac{Q}{ε}\)[本]、電束\(\phi\)[C]

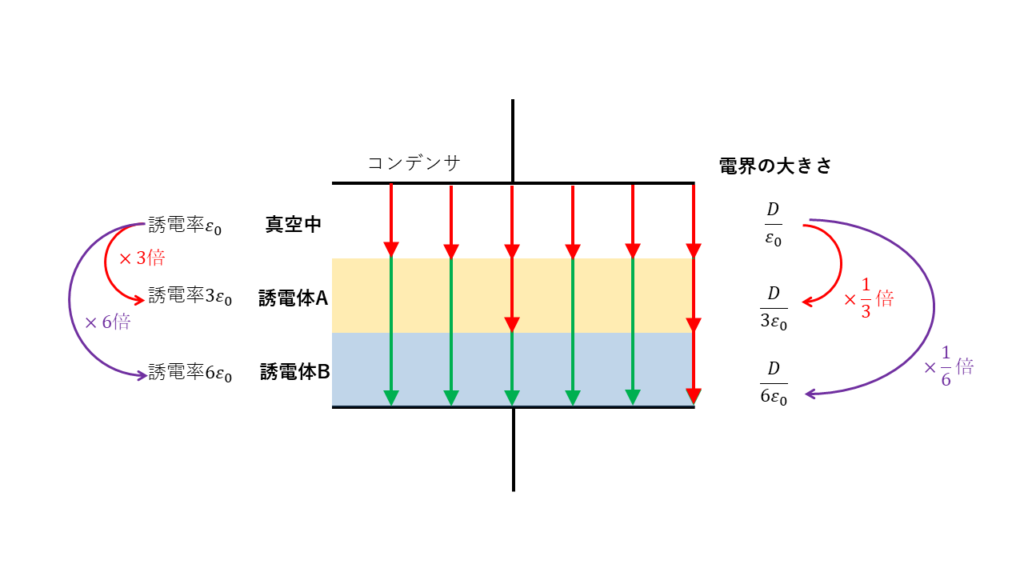
電気力線の密度を電界と呼びましたが、電束の密度は電束密度と呼びます。

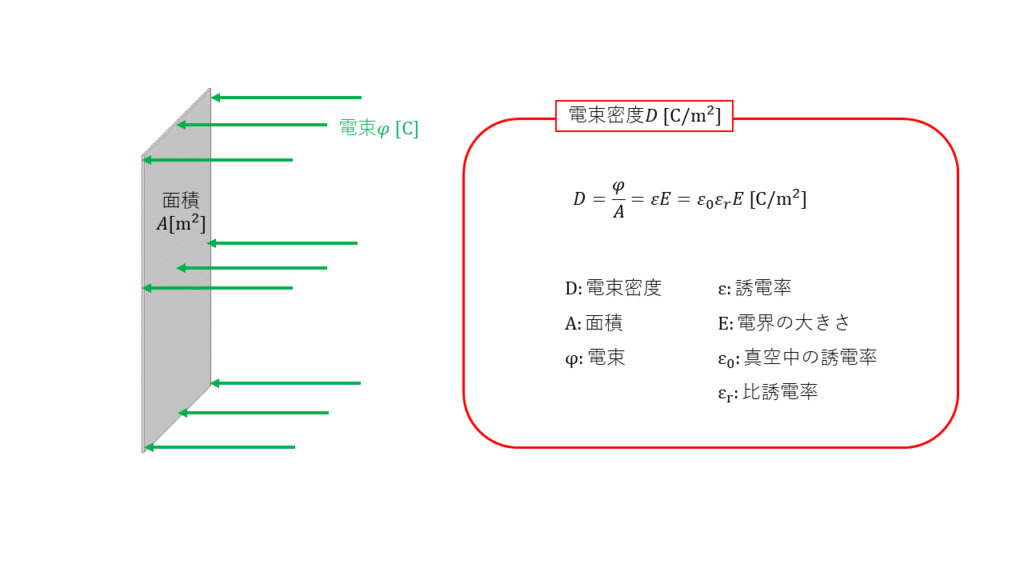
電界の大きさは、電束密度を誘電率で割ることで求めることができます。そのため、異なる誘電率の並ぶ場合でも電束密度の考え方を用いれば簡単に考えることができます。

まとめ