直流電動機は、家電などの身近なところでは多く使用されています。
電験の学習では全ての回転機械の動作原理を理解するための基礎となる内容です。
電験3種の機械科目では、必ず問1で出題されます。また、各電動機の特性を問われる問題にも度々出題されています。
覚えることの多い内容ですが、計算問題はパターン化されているため得点源にしやすテーマです。
- 直流電動機の構造
- 直流電動機の回転する原理
- 直流電動機のトルクと出力の計算
\( T = \displaystyle \frac{pZ}{2 \pi a} \phi I_a = K_2 \phi I_a \) - 各直流電動機の等価回路
- 直流電動機の速度特性とトルク特性
それでは、学習を始めましょう!
直流電動機の回転原理
直流電動機はフレミングの左手の法則を応用して回転する力を得ています。
フレミングの左手の法則とは、「磁界中を流れる電流には、磁界と電流に対して垂直な方向に力が働く」というものです。電流、磁界、働く力の向きは下の図1に示すようになります。
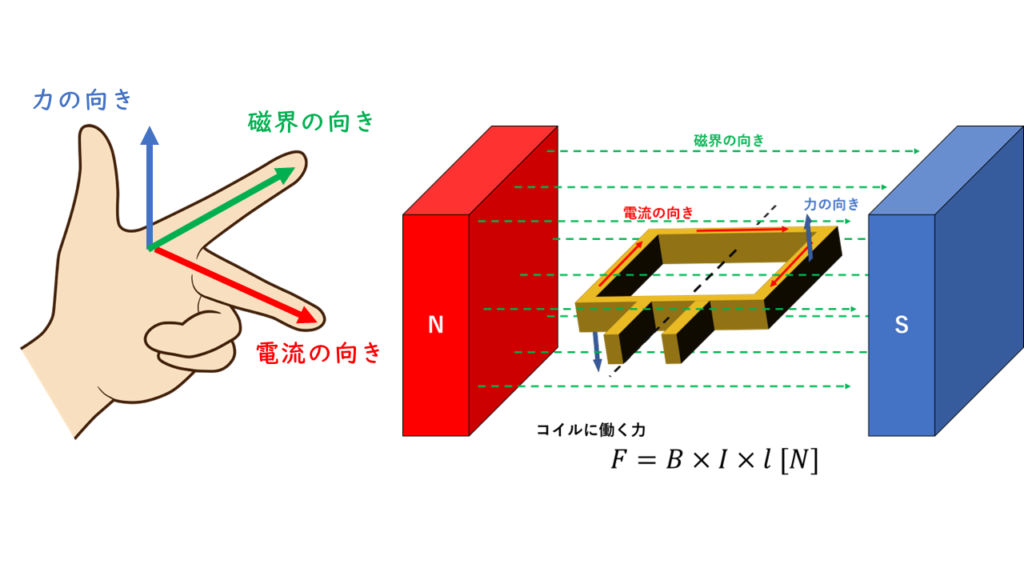
磁界の大きさ(磁束密度)をB[T]、電流の大きさをI[A]、磁界中にある導体の長さをl[m]とするとき力(電磁力)の大きさF[N]は次の式で表すことができます。
電磁力の大きさ:\( F = B \times I \times l \) [N]
実際の直流電動機は、コイル(導体)に働く電磁力を利用して回転する構造となっています。
コイルを電源と直接接続してしまうと、コイルが半周回転したときに電流の向きが逆向きになり今までとは反対方向の力が働いてしまいます。
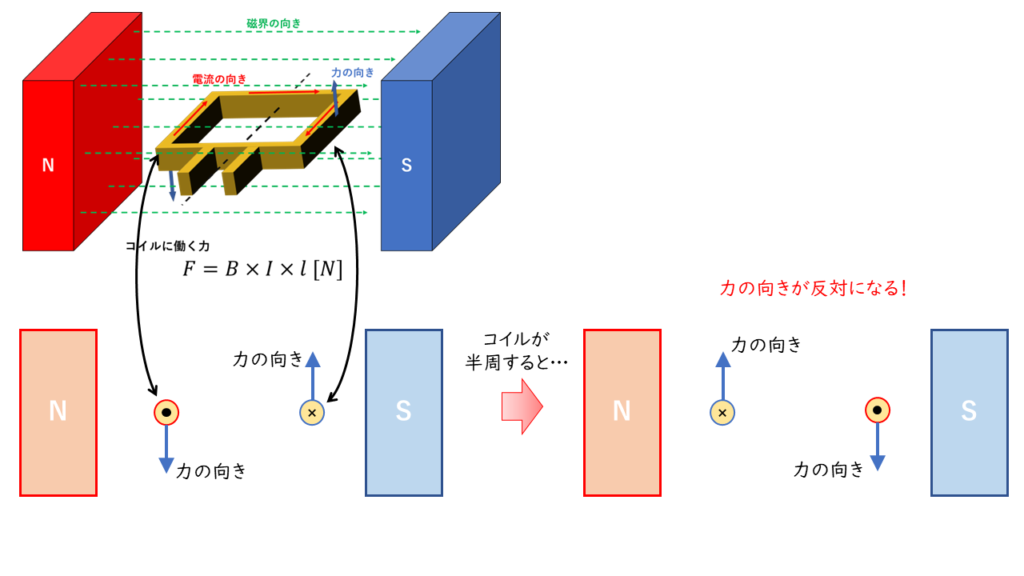
そこで、コイルに働く力を一定の方向にするために半周ごとにコイルに流れる電流の向きを入れ替える装置を取り付けます。それが、「整流子」と「ブラシ」です。
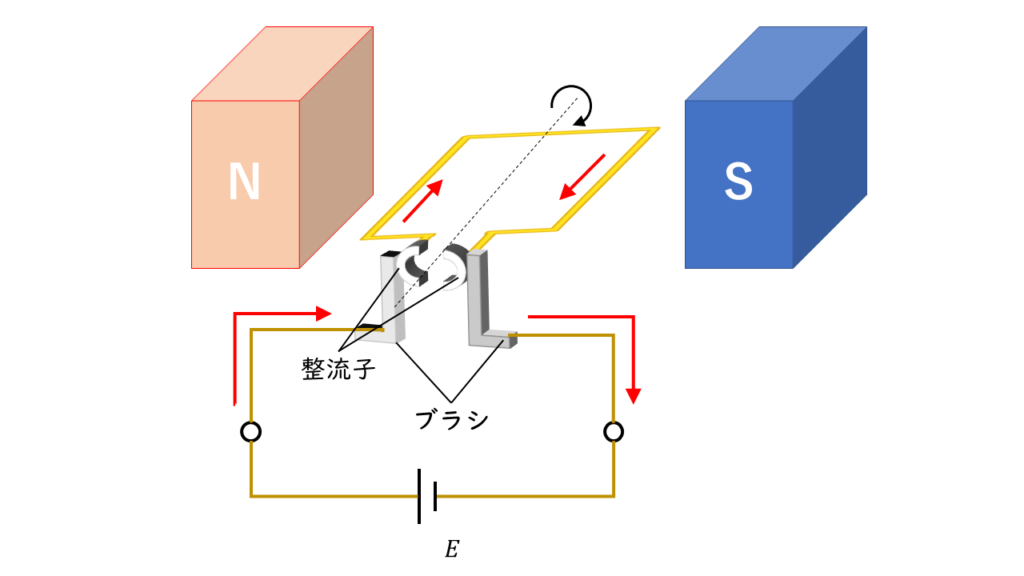
直流電動機の構造
直流電動機の基本的な構造は図2に示すような構造となっています。
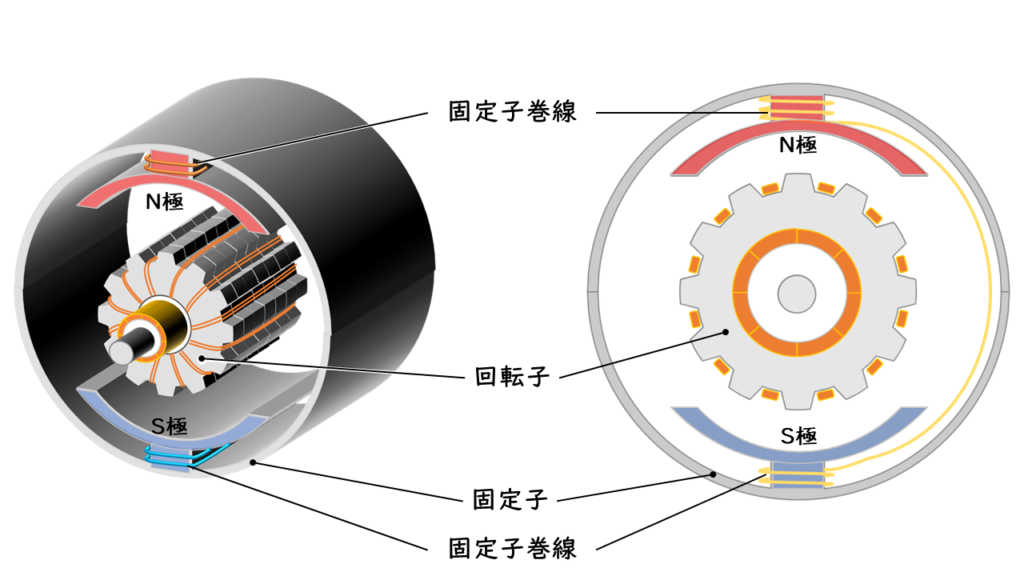
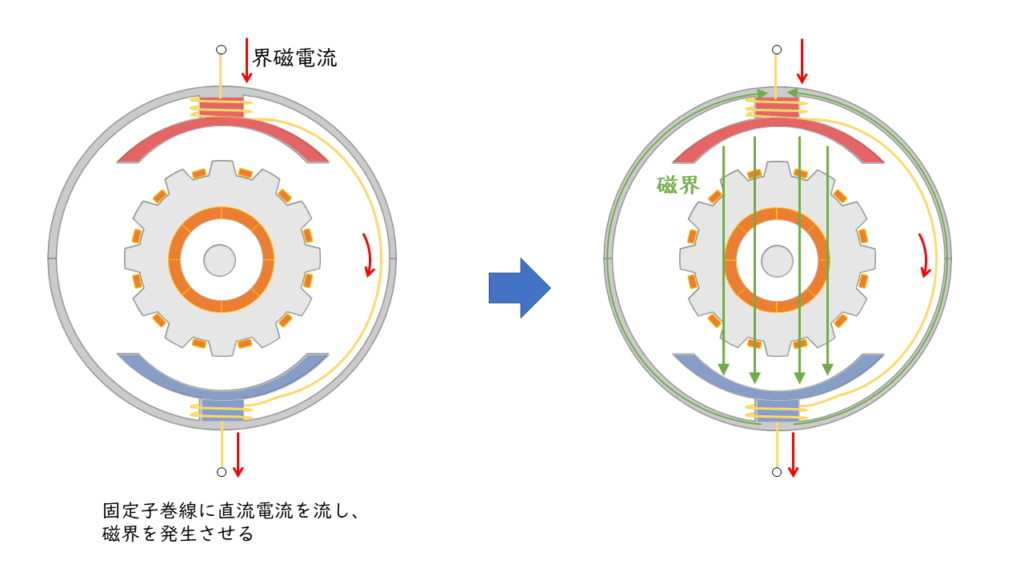
直流電動機では、固定子が磁界を作る部分になります。
固定子のコイルに電流が流れると電磁石になり、磁界を発生させます。このように磁界を作る装置のことを「界磁(かいじ)」といい、界磁に流れる電流を「界磁電流」と呼びます。
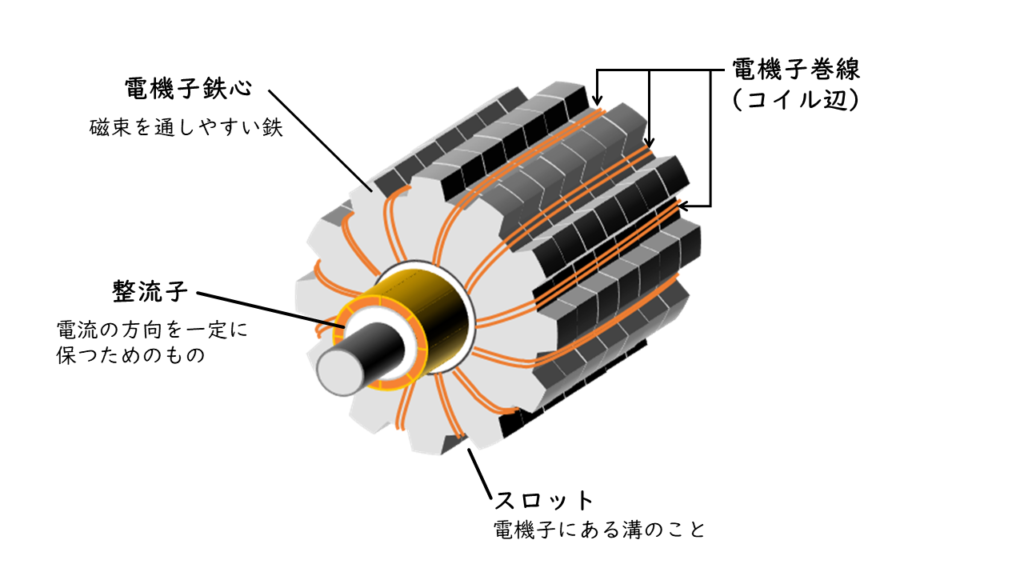
一方、回転子は「電機子」とも呼ばれ、図3のような構造をしています。
電機子巻線の巻き方は「重ね巻」と「波巻」の2種類があります。
重ね巻
重ね巻(並列巻)は初めのコイルの巻き終わりを、次のコイルの巻き始めと接続し(重ねて)、整流子片につなげて、次々に接続していく巻き方です。
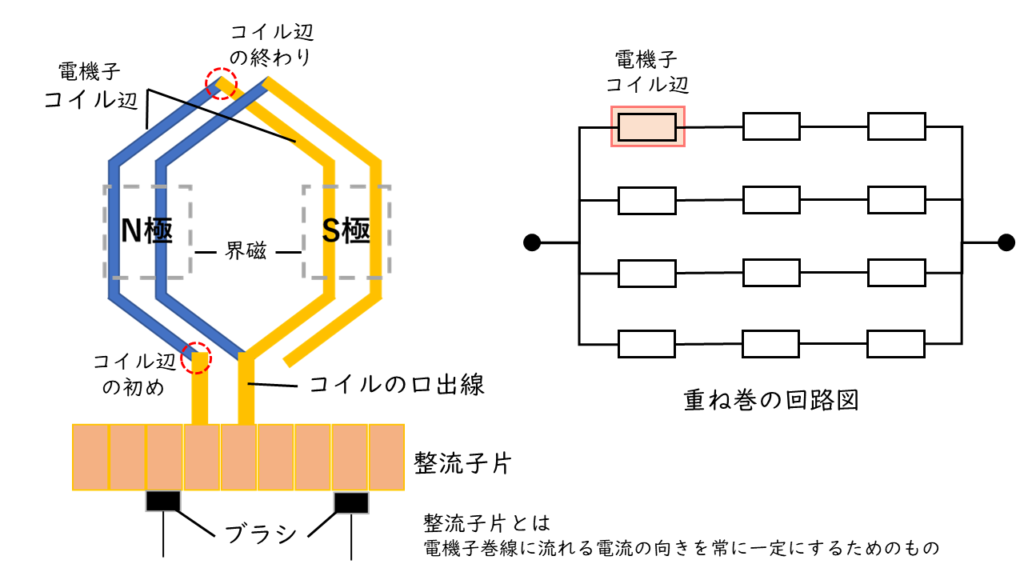
・並列回路数\(a\)と磁極数\(p\)は等しくなる \(a = p\)
・並列回路数とブラシの数は等しくなる
・低電圧、大電流に適している
波巻
波巻(直列巻)は、コイルの接続した形が波のようになっている接続方法です。
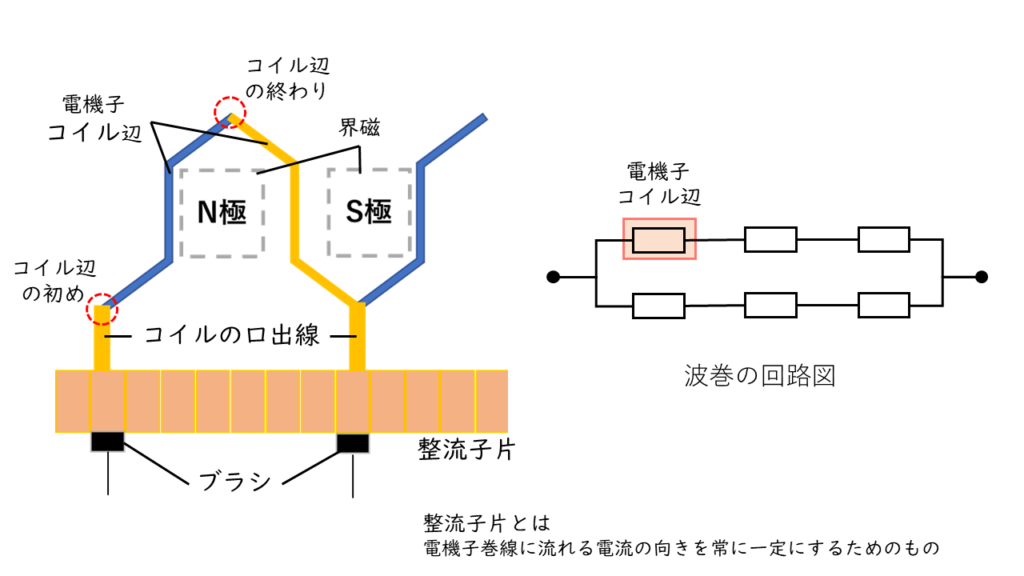
・並列回路数は常に2となる
・ブラシの数もブラシと同じ2となる
・高電圧、小電流に適している
直流電動機機の等価回路
直流電動機には主に「他励式」「分巻式」「直巻式」「複巻式」の4種類があります。
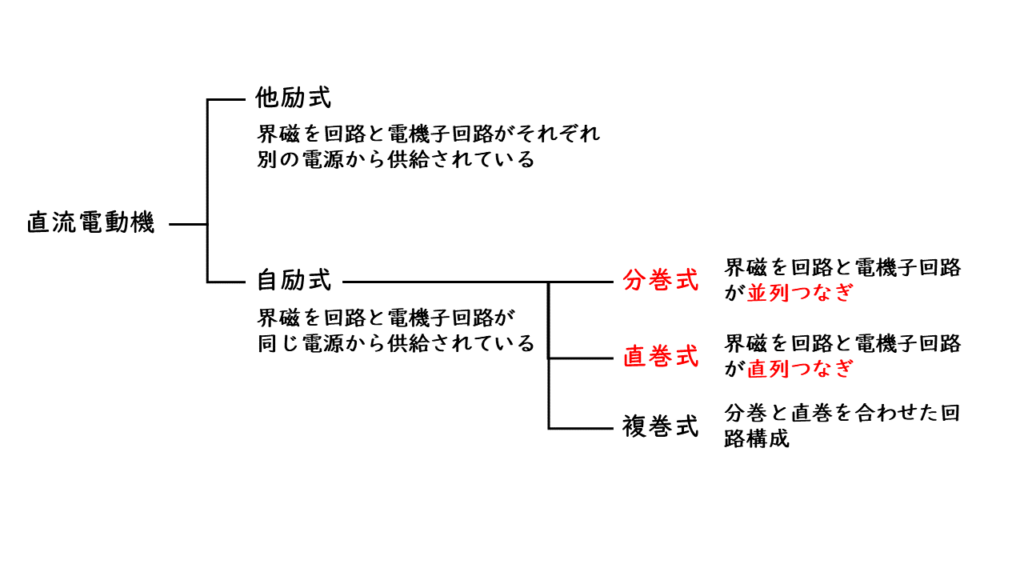
電験3種では特に分巻電動機、直巻電動機の計算問題が出題されます。しっかり覚えておきましょう!
他励式直流電動機
他励式は、磁界を発生させるための界磁回路と回転子の電気子回路がそれぞれ異なる電源から電気の供給を受ける構造の直流電送機です。
模式的に表した回路の構造は図4のようになります。
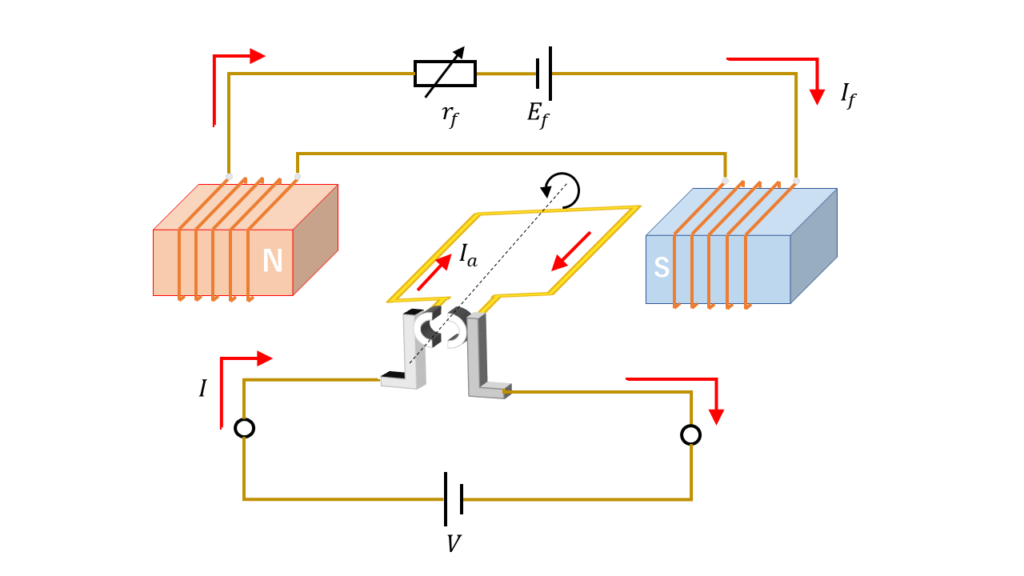
図4の回路を等価回路図に表すと図5の様になります。
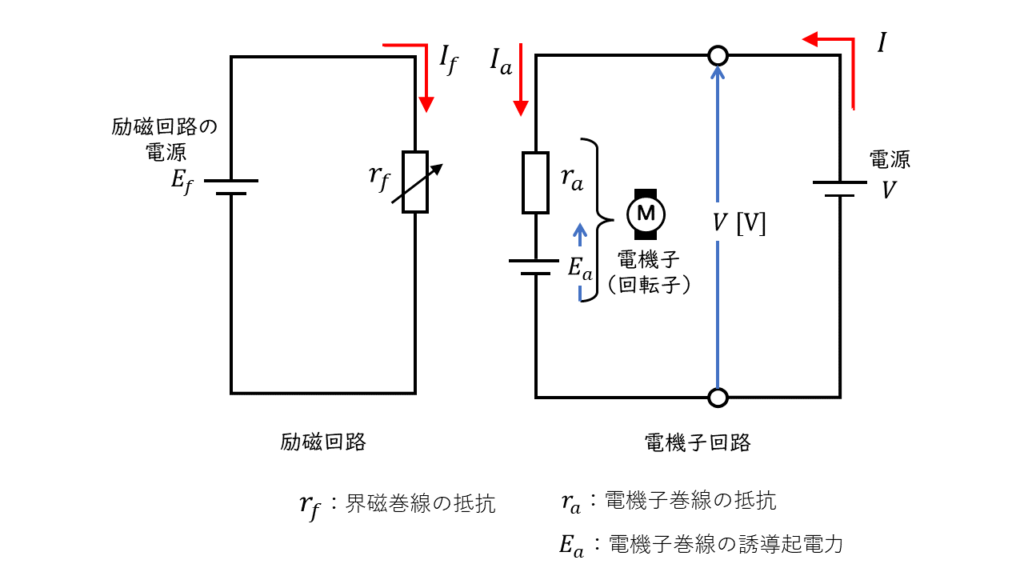
直流電動機の電気子が磁界の中を回転すると、電気子コイルで電磁誘導が起こり電源電圧とは逆向きの誘導起電力\(E_a\)[V]が発生します。回路を流れる電流と電圧の関係式は以下の様になります。
\(E_a = V – r_a \times I_a \)
\(I_f = \displaystyle \frac{E_f}{r_f}\)
\(I_a = I \)
自励式分巻直流電動機
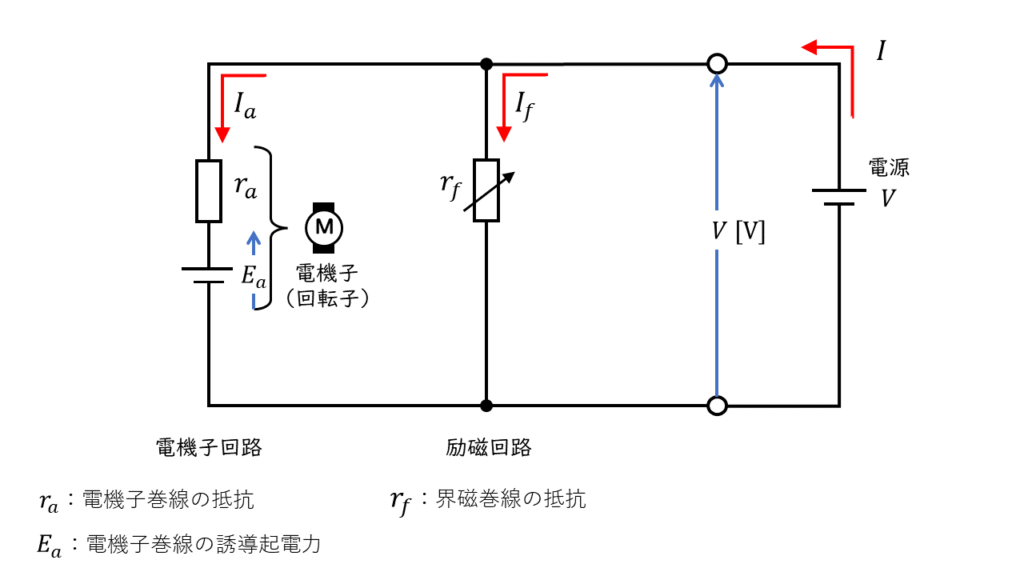
分巻電動機(ぶんまきでんどうき)は、電気子回路と界磁回路が並列接続され、同じ電源から電気の供給を受けている構造の直流電動機です。
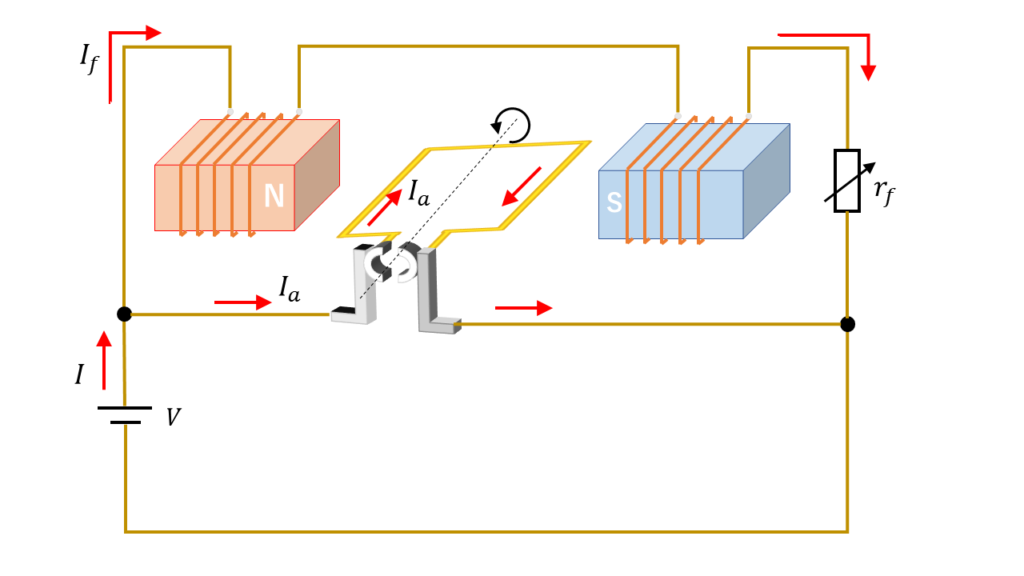
図6の回路を等価回路図に表すと図7のようになります。
\( E_a = V -r_a \times I_a \)
\( I_f = \displaystyle \frac{V}{r_f} \)
\( I_a = I – I_f \)
電機子回路と界磁回路が並列接続されているため、それぞれの回路に電源の電圧と同じ大きさの電圧が印加されます。
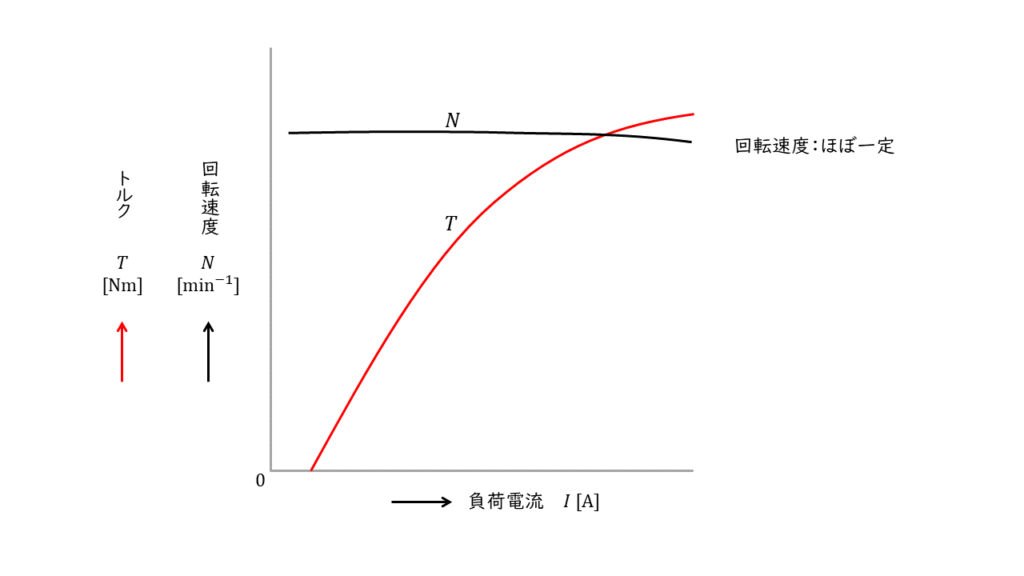
そのため、負荷電流が変化しても界磁回路には影響はなく、回転速度をほぼ一定に保つことができる特徴を持ちます。
自励式直巻直流電動機
直巻電動機(ちょくまきでんどうき)は、電機子回路と界磁回路が直列に接続されており、同じ電源から電気の供給を受ける構造の直流電動機です。
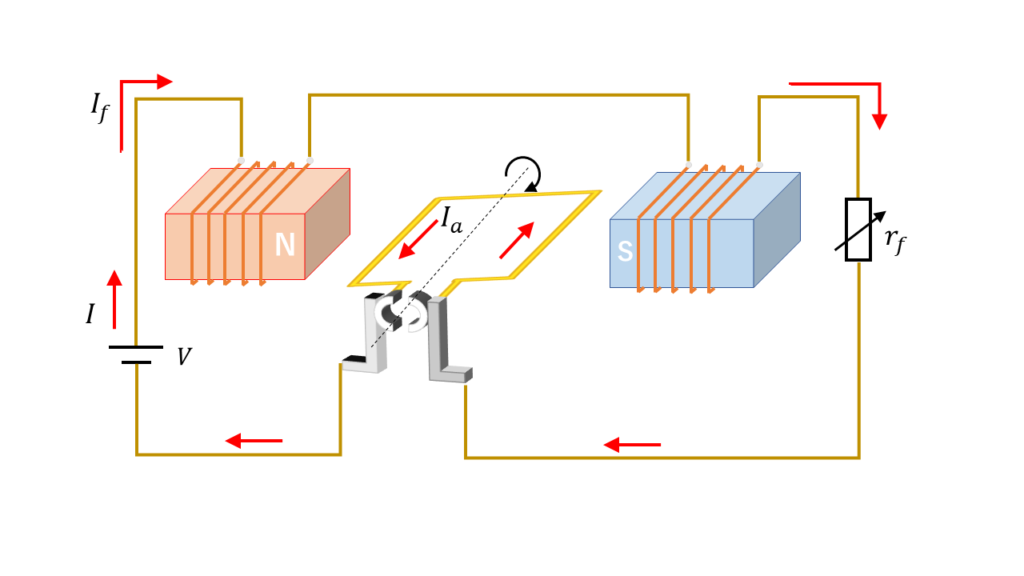
図8の回路を等価回路図に表すと図9のようになります。
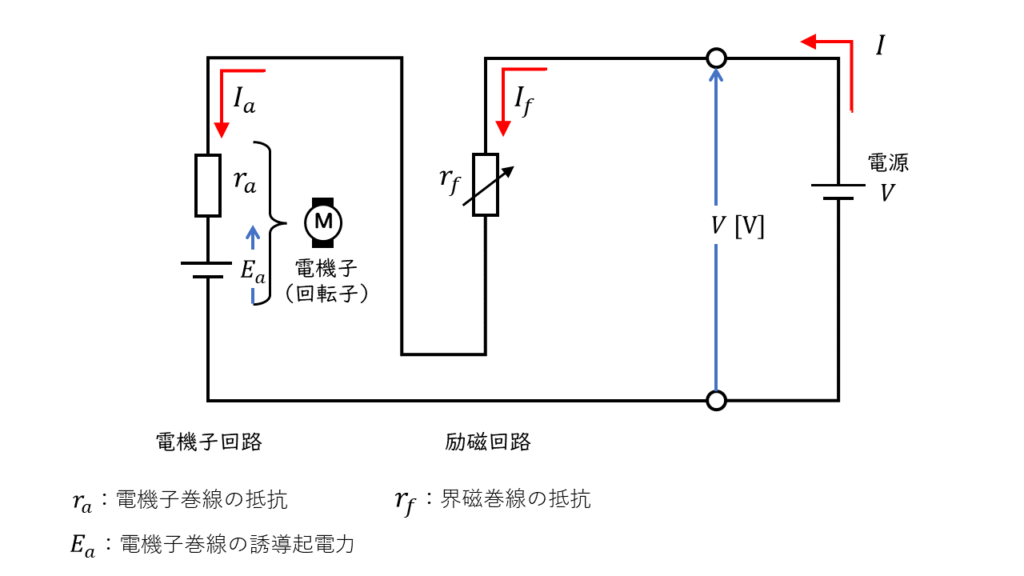
\(E_a = V – \left( r_a + r_f \right) \times I_a \)
\( I_a = I = I_f \)
電気子回路と界磁回路が直列に接続されているため、負荷が大きくなる(重たくなる)と負荷電流と界磁電流は大きくなります。そのため、トルクは大きくなりますが、回転速度は遅くなります。
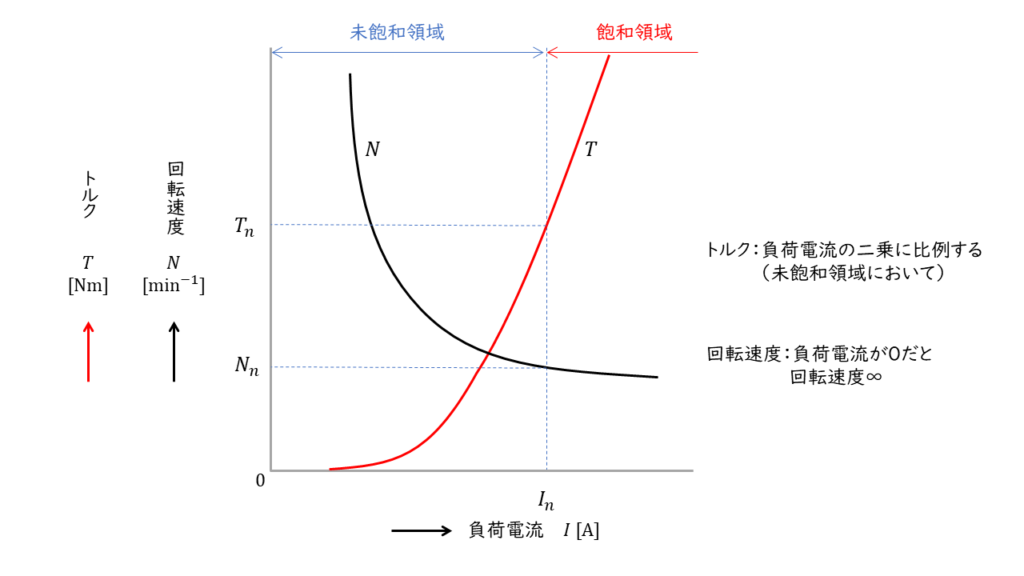
直流電動機のトルクと出力
\( T = \displaystyle \frac{pZ}{2 \pi a} \phi I_a = K_2 \phi I_a\)
\( P_o = \omega T = 2\pi \displaystyle \frac{N}{60} T = E_a I_a \)
電動機のトルク:\(T\)[N・m]
磁極数:\(p\) ,並列回路数:\(a\)
コイル辺の数:\(Z\)
1極あたりの磁束:\(\phi\)[wb]
電機子電流:\(I_a\) [A]
電動機の出力:\(P_o\)[W]
角速度:\(\omega\)[rad/s]
回転速度:\(N\)[\(\rm min ^{-1}\)]
誘導起電力:\(E_a \)[V]
定数:\(K_2\)
成り立ちを理解するにはやや複雑な解説が必要です。この公式は暗記しておきましょう!
磁極数\(p\),並列回路数\(a\),コイル辺の数\(Z\)は一度電動機を製作してしまうと変更することができないためひとまとめにして、定数\(K_2\)で表す場合があります。
トルクとは
回転させる仕事のことをトルクといいます。
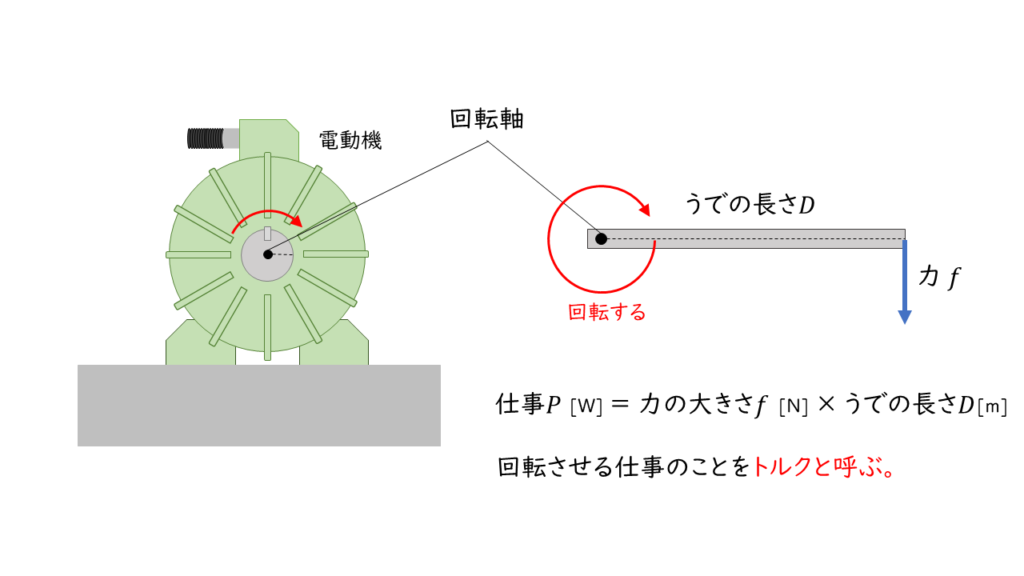
電動機は電気のエネルギーを回転する仕事に変換する機械装置と考えることができます。
電験3種の試験では、等価回路と組合わせて、トルクや出力を計算させる問題が出題されます。
公式を覚えることは大切ですが、等価回路も合わせて覚えておきましょう。



コメント