直流電動機の速度特性やトルク特性、速度制御に関する問題は直流機の計算の次に出題頻度の高いテーマです。
- 回転速度の導き方
\( \begin{align} N &= \displaystyle \frac{E_a}{K_1 \phi} \\ &= \displaystyle \frac{V-r_a Ia}{K_1 \phi} \ \ or \ \ \displaystyle \frac{V – \left( r_a + r_f \right) I_a}{K_1 \phi} \end{align}\) - 分巻電動機、直巻き電動機の特性
- 始動・制動方法
- 速度制御方法
各電動機の特性は等価回路を使用することで簡単に考えることができます。
一つずつ整理していけば、決して難しい内容ではないので得点源となります。
それでは、学習を始めてきましょう。
直流電動機の回転速度
他励式:\( N = \displaystyle \frac{E_a}{K_1 \phi} = \displaystyle \frac{V – r_a I_a}{K_1 \phi} \)
分巻式:\( N = \displaystyle \frac{E_a}{K_1 \phi} = \displaystyle \frac{V – r_a I_a}{K_1 \phi } \)
直巻式:\( N = \displaystyle \frac{E_a}{K_1 \phi} = \displaystyle \frac{V – \left( r_a + r_f \right) I_a }{K_1 \phi} \)
直流電動機の回転速度は、誘導起電力の式を変形していくことで導き出すことができます。
誘導起電力:\( E_a = \displaystyle \frac{pZ}{60a}\phi N \)
磁極数p ,コイル辺の数Z ,並列回路数a は直流電動機を製作した時点で変更することができないため、定数とみなして扱います。
\( \displaystyle \frac{pZ}{60a} = K_1 \)
定数\(K_1\)は直流電動機の構造上の定数となります。この定数を誘導起電力の式に当てはめると、
\( \begin{align} E_a &= K_1 \phi N \\ \\ N &= \displaystyle \frac{E_a}{K_1 \phi} \end{align} \)
となります。
誘導起電力\(E_a\)は等価回路図より、それぞれ以下のようになります。
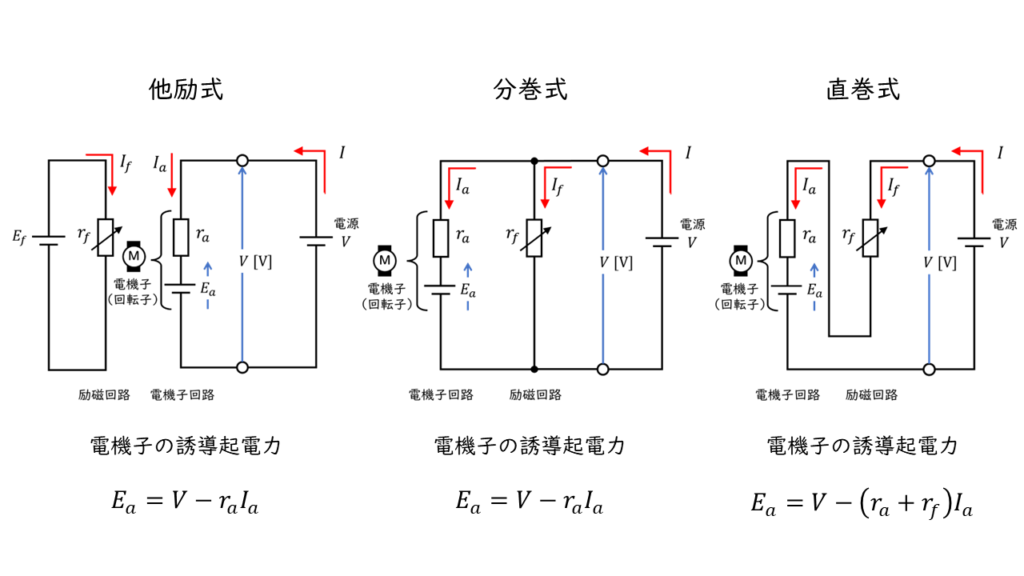
したがって、各直流電動機の回転速を表す式は
他励式:\( N = \displaystyle \frac{E_a}{K_1 \phi} = \displaystyle \frac{V – r_a I_a}{K_1 \phi} \)
分巻式:\( N = \displaystyle \frac{E_a}{K_1 \phi} = \displaystyle \frac{V – r_a I_a}{K_1 \phi } \)
直巻式:\( N = \displaystyle \frac{E_a}{K_1 \phi} = \displaystyle \frac{V – \left( r_a + r_f \right) I_a }{K_1 \phi} \)
となります。
分巻電動機の特徴
負荷電流と回転速度の関係
分巻電動機の回転速度は、
\( N = \displaystyle \frac{V – r_a I_a}{K_1 \phi } \)
と表すことができました。
電動機に接続する電源電圧\(V\)[V]と界磁抵抗\(r_f\)[Ω]が一定であるという条件で考えると
\( I_f = \displaystyle \frac{V}{r_f} \)
となり、界磁電流の大きさも一定になります。
磁束\(\phi\)を作り出す磁気回路において、コイルの巻数\(n\) ,固磁気抵抗\(R_m\)は一定であると考えられるので、界磁磁束は
磁束:\( \phi =\displaystyle \frac{n I_f }{R_m} =\) 一定
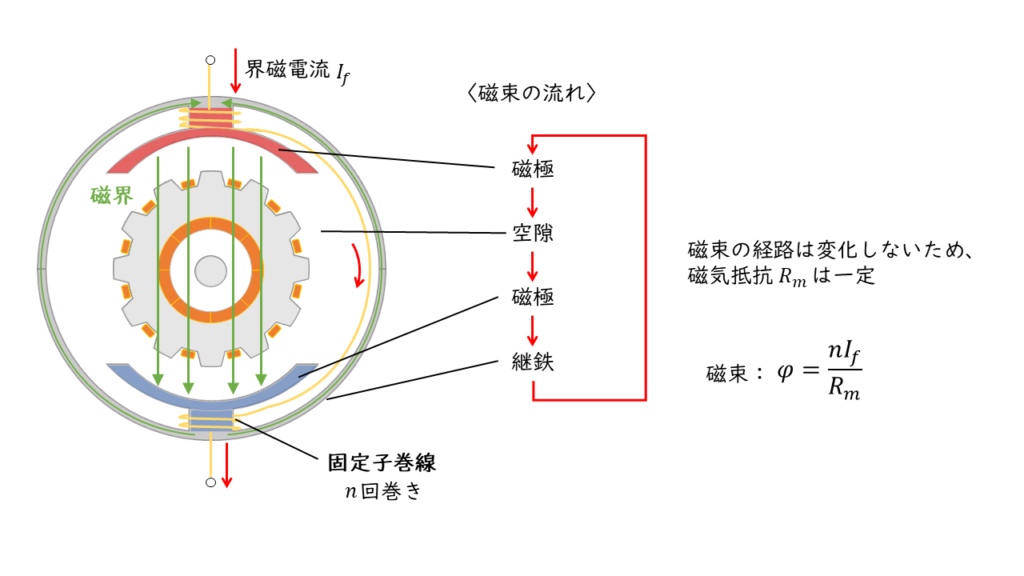
となるため、回転速度Nは電気子電流\(I_a\)の変化のみによって回転数が変化します。
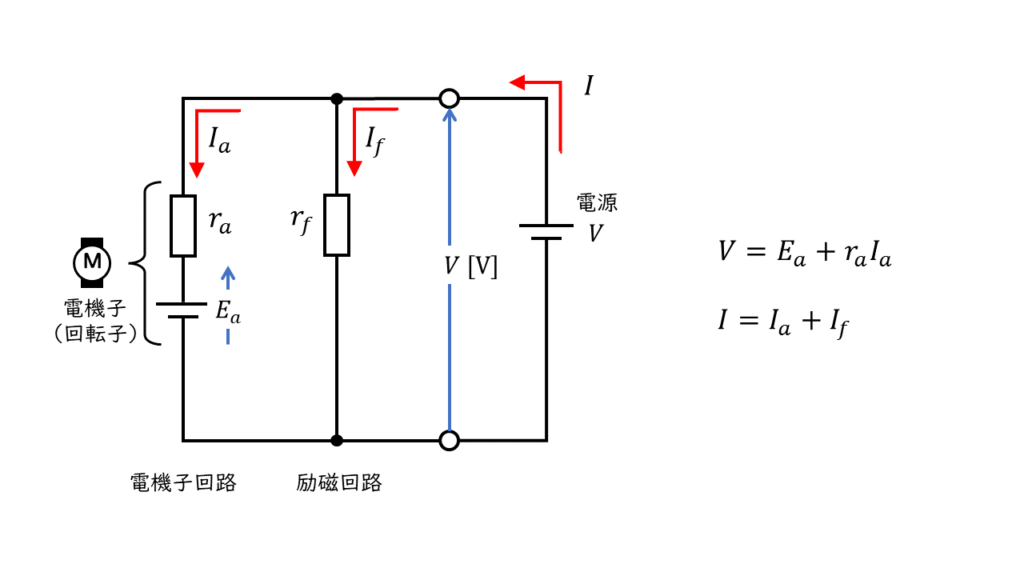
\( \begin{align} N &= \displaystyle \frac{V – r_a I_a }{K_1 \phi} = \displaystyle \frac{V – r_a \left( I-I_f \right)}{K_1 \phi} \\ \\ &= \displaystyle \frac{V-r_a I}{K_1 \phi}+\frac{V-r_a I_f}{K_1 \phi} \end{align} \)
と書き表すことができるため、回転速度Nは負荷電流が増加すると、わずかに回転速度が減少します。
負荷電流とトルクの関係
直流電動機のトルクの公式は
\( T = \displaystyle \frac{pZ}{2 \pi a}\phi I_a = K_2 \phi I_a \)
で表すことができました。
先ほどの回転速度でも確認したように、磁束\(\phi\)は一定の大きさであるため、トルク\(T\)の大きさは電機子電流\(I_a\)に比例します。

負荷電流との関係を表すために、トルク\(T\)の式を変形すると
\( \begin{align} T = K_2 \phi I_a &= K_2 \phi \left( I – I_f \right) \\ \\ &= K_2 \phi I – K_2 \phi I_f \end{align} \)
となりトルクは負荷電流に比例する式が得られます。
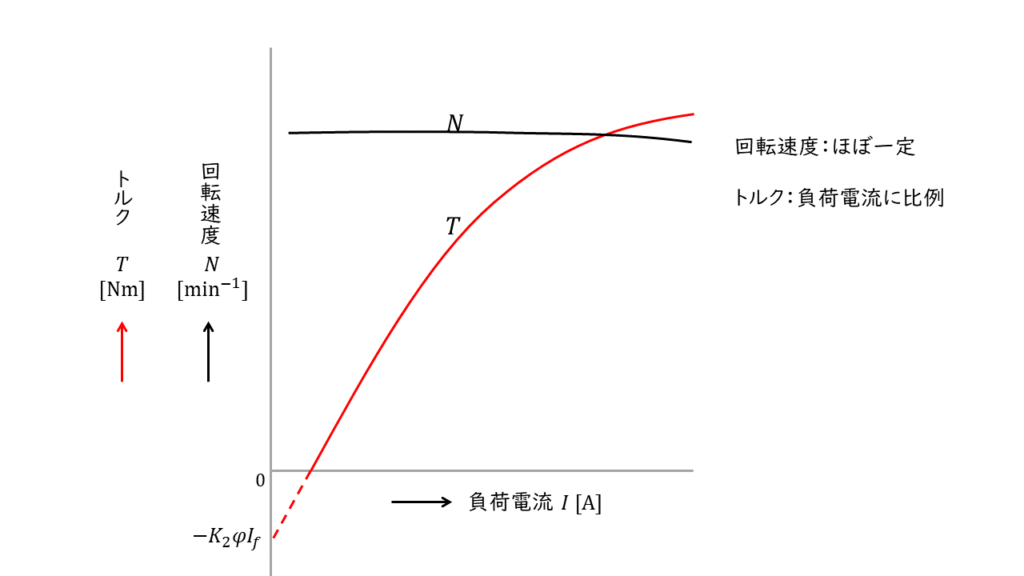
・回転速度はほぼ一定
※負荷電流の増加によりわずかに減少する
・トルクは電機子電流の大きさに比例する
直巻電動機の特徴
負荷電流と回転速度の関係
直巻き電動機の回転速度を表す式は、
\( N = \displaystyle \frac{E_a}{K_1 \phi} = \displaystyle \frac{V-\left(r_a+r_f \right)I_a}{K_1 \phi} \)
です。
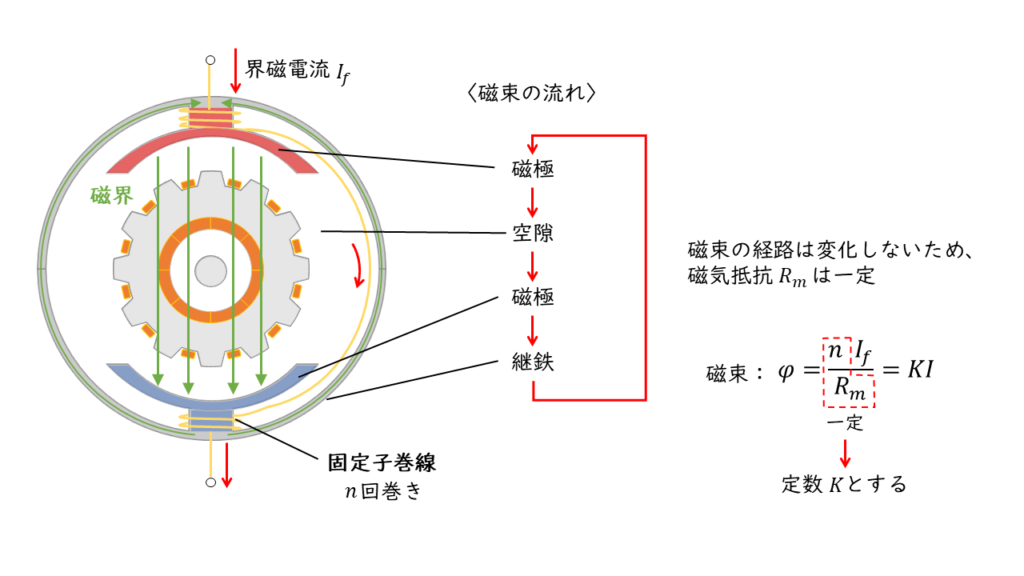
磁束\(\phi\)は界磁巻線の巻数を\(n\) ,界磁回路の磁気抵抗を\(R_m\)とすると
磁束:\( \phi = \displaystyle \frac{n I_f}{R_m} \)
と表すことができます。直巻き電動機では、界磁回路と電機子回路が直列に接続されているので、
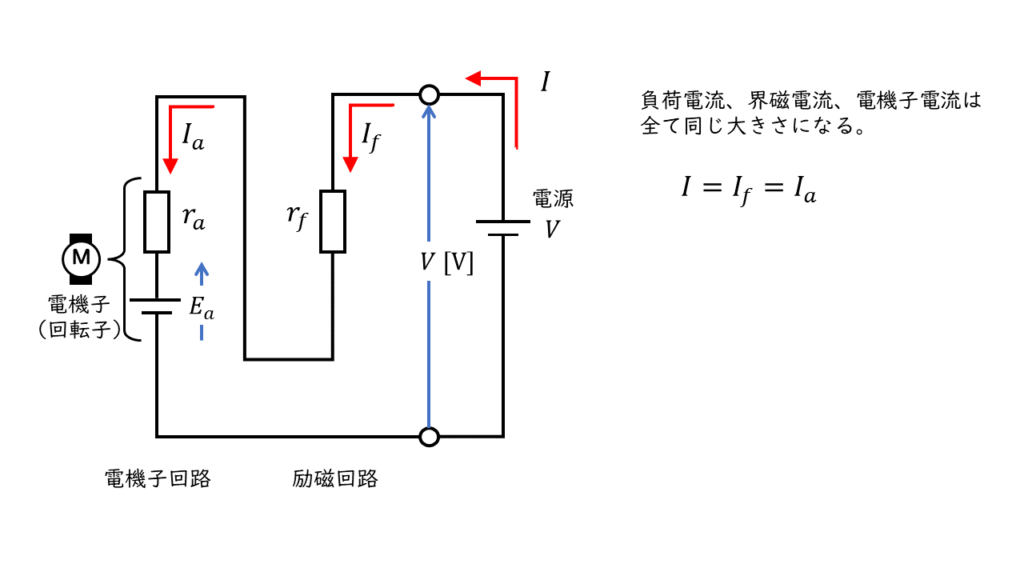
となります。
ここで、電源電圧\(V\)[V]と界磁抵抗\(r_f\) [\( \rm \Omega\)]は一定という条件とすると回転速度の式は次のように考えることができます。
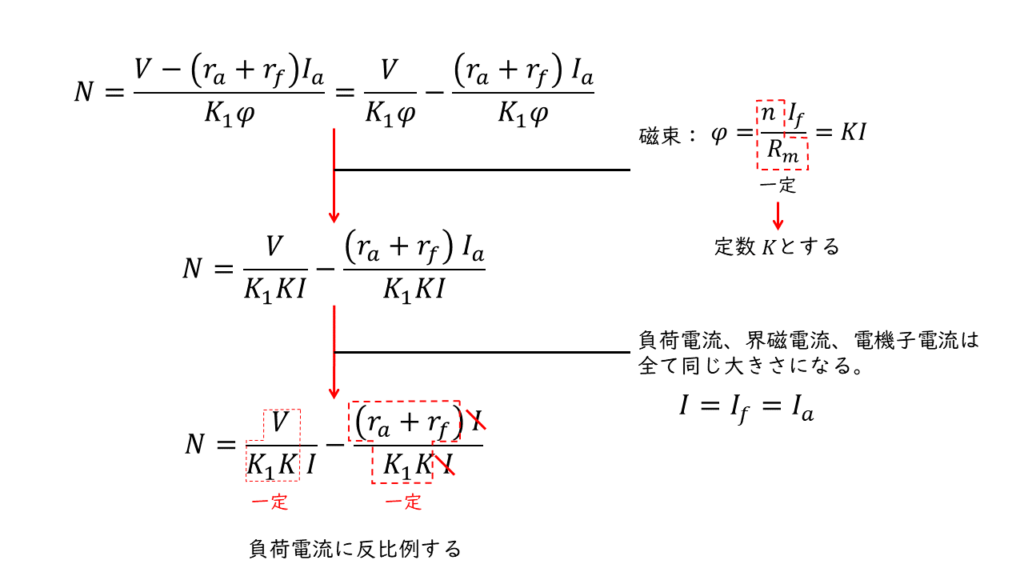
したがって、直巻電動機の回転速度は負荷電流に反比例します。
負荷電流とトルクの関係
直流電動機のトルクの公式は
\( T = \displaystyle \frac{pZ}{2 \pi a}\phi I_a = K_2 \phi I_a \)
で表すことができました。
界磁磁束\(\phi\)は回転速度の時と同じように考えることができるため、
磁束:\( \phi = \displaystyle \frac{nI}{R_m} = KI\)
と表すことができます。
したがって、トルク\(T\)は
\(T = K_2 \phi I_a = K_2 \times K I \times I_a \)
となります。
直巻電動機では、負荷電流と電機子電流の大きさは同じであるため、
\( T = K_2 K I^2 \)
と表すことができ、トルクは負荷電流の二乗に比例することが分かります。
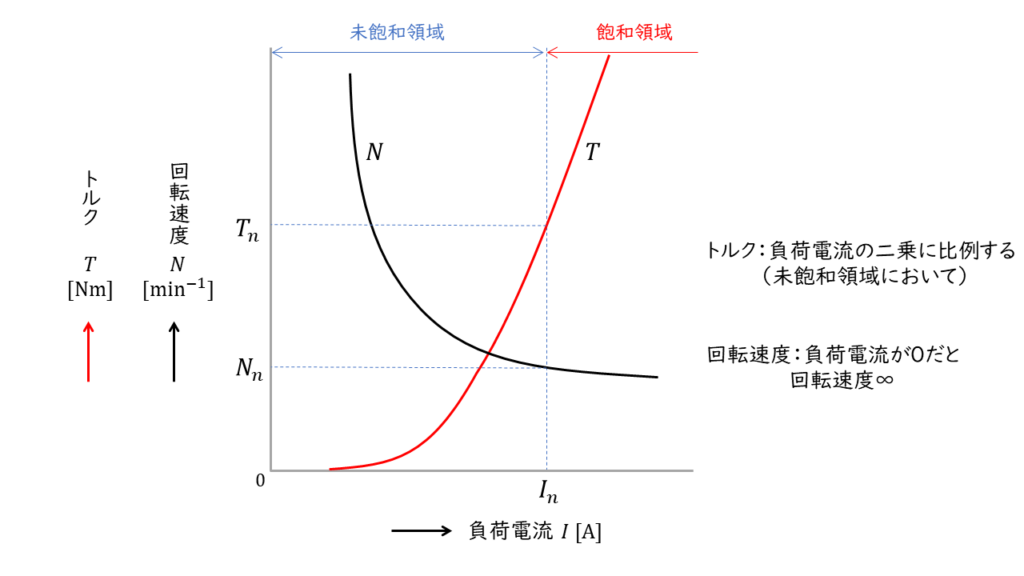
・負荷電流が無い時は、回転速度は \( \infty \)
・トルクが負荷電流の二乗に比例する
直流電動機の始動と制動
始動方法
直流電動機は、始動時には電機子が回転していないため、電機子の誘導起電力(逆起電力)\(E_a\)が0[V]になります。
また、電機子抵抗\(r_a\)も小さい値のため、始動時に大きな電機子電流が流れます。
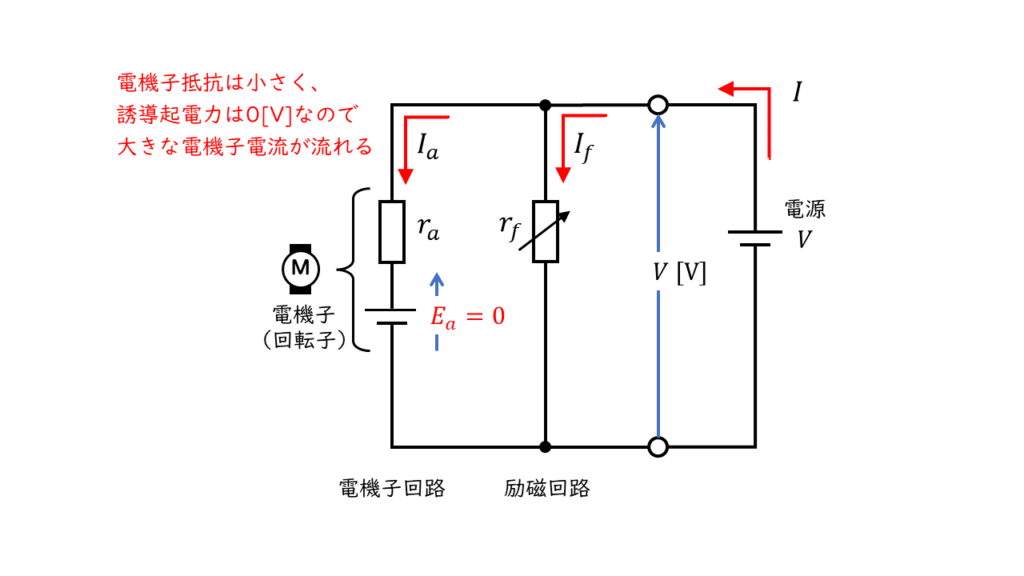
始動時の電機子電流:\( I_a = \displaystyle \frac{V}{r_a} \)
始動時に流れる大きな電機子電流のことを「始動電流」といいます。
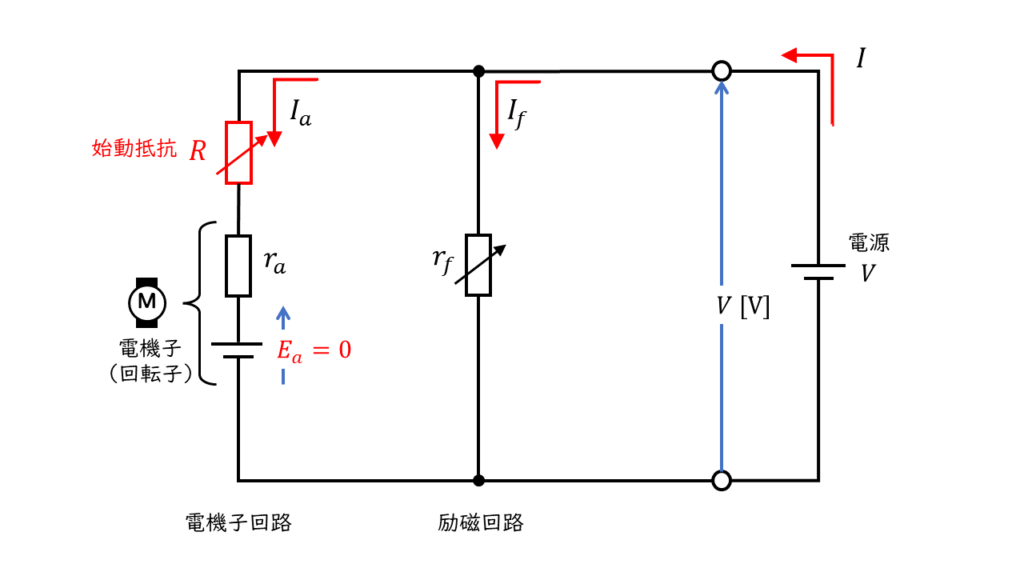
このままでは、過電流継電器が動作して始動できなかったり、始動電流によって巻線が焼損したりする恐れがあります。そこで、始動電流を小さく抑えるために、始動時には電機子抵抗に直列に「始動抵抗」を挿入します。
制動方法
制動とは電動機を停止させるブレーキのことを言います。電気的な制動方法には以下の3があります。
- 発電制動
- 回生制動
- 逆転制動
発電制動
電源から切り離して抵抗を接続する方法です。
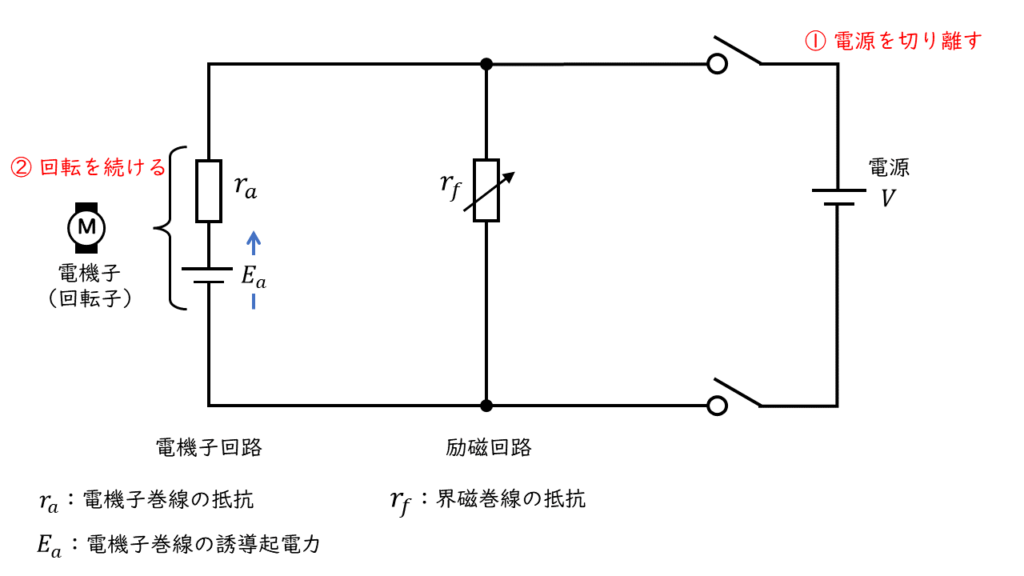
電源をOFFにしてもしばらくの間は惰性で回転し続けます。
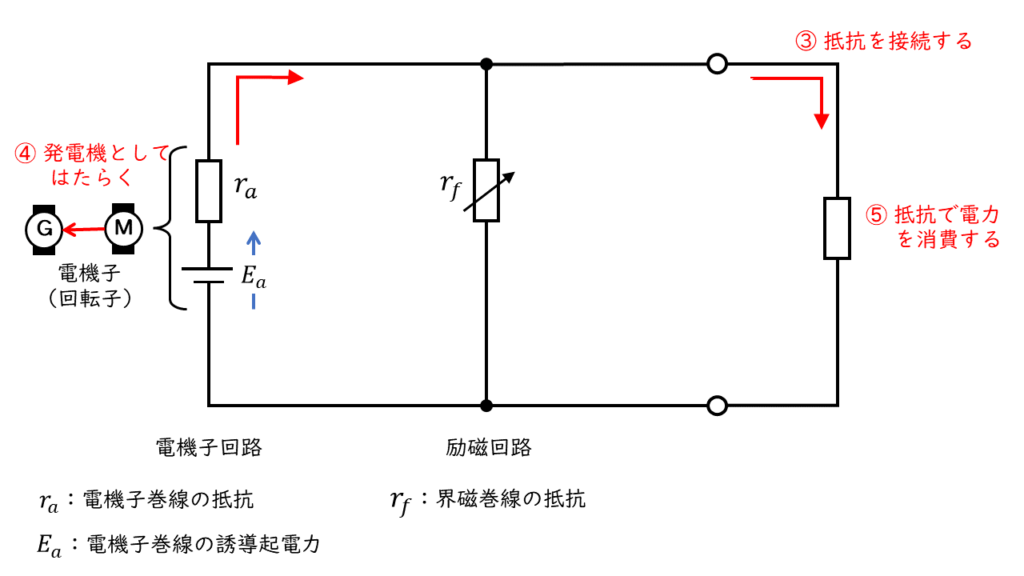
回転を続けいる間、電機子は逆起電力(誘導起電力)を発生させ続けるので、電動機を発電機として運転し、発電した電力を接続した抵抗で消費させてブレーキを掛ける方法です。
回生制動
電動機を発電機として運転し、発電した電力を電源に戻して他の用途で電力を消費するブレーキ方法です。
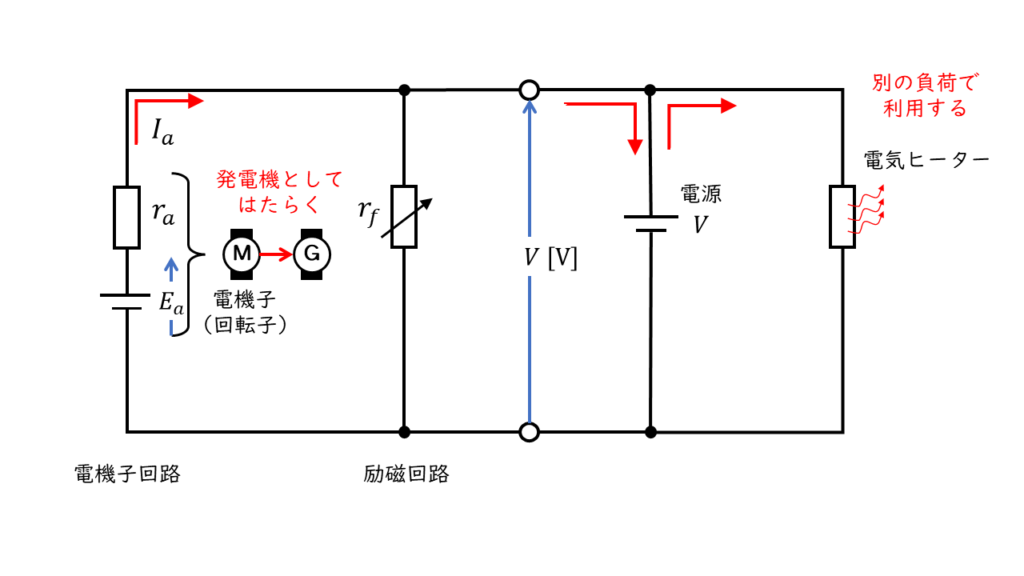
発電制動との違いは、電源から切り離していないことです。
逆転制動
電機子端子を逆向きに接続して、逆回転方向のトルクを発生させてブレーキをかける方法です。
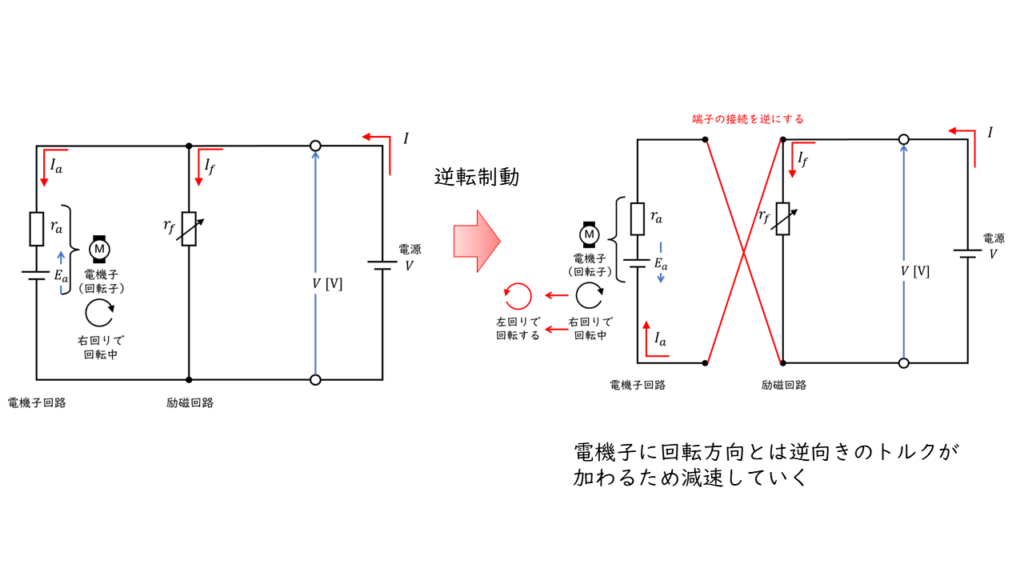
直巻き電動機が回転中の速度制御
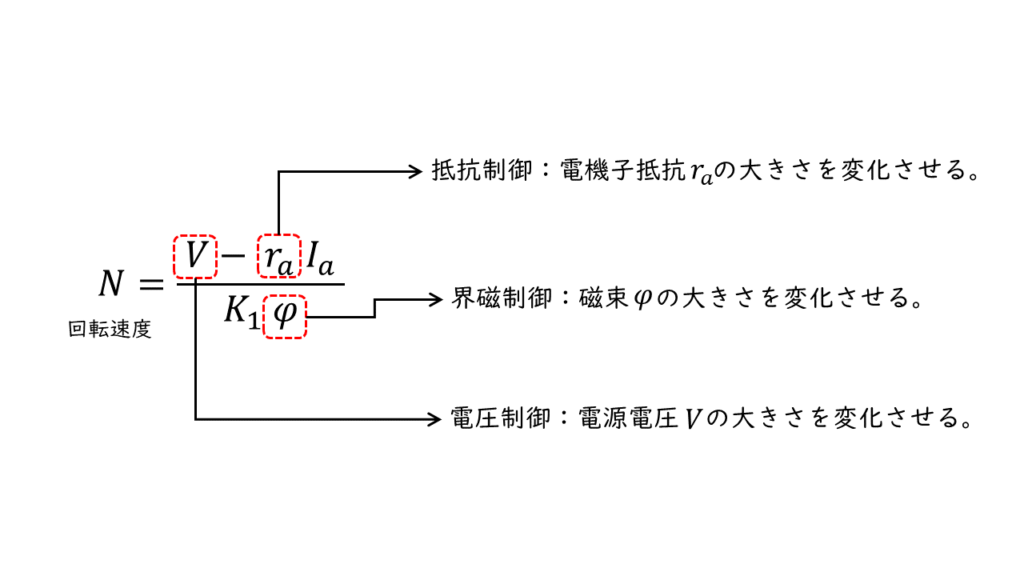
電動機の回転速度を変化させることを「速度制御」といいます。直流電動機の回転速度は公式より
\( N = \displaystyle \frac{V – r_a I_a}{K_1 \phi} \)
で表されるため、以下の要素を変化させることで回転速度変化が可能になります。
抵抗制御:電機子と直列に抵抗を挿入して電気子抵抗\(r_a\)の大きさを変化させることで、
回転速度を変化させる方法です。
界磁制御:界磁電流の大きさ\(\phi\)を変化させて、
磁束の大きさを変化させることで回転速度を変化させる方法です。
電圧制御:電源電圧の大きさ\(V\)を変化させることで、回転速度を変化させる方法です。
電圧制御には、「ワードレオナード方式」、「静止レオナード方式」、
「直流チョッパ方式」の3つがあります。




コメント