
鳳-テブナンの定理てどんな時に役立つの?
こんばんは、ももよしです。
理論の参考書に必ず登場する『鳳-テブナンの定理』について解説します。
要点
・鳳⁻テブナンの定理とは
複雑な回路を内部抵抗をもつ電圧源とみなし計算を簡単にする手法
複雑な回路を内部抵抗をもつ電圧源とみなし計算を簡単にする手法
主な使用場面としては、任意の場所の電流を求める場合、二端子間の電圧を求める場合及び地絡電流計算などがあります。
目次
鳳⁻テブナンの定理の使用例
例1複数の電源が並列接続されている回路の電流を求める
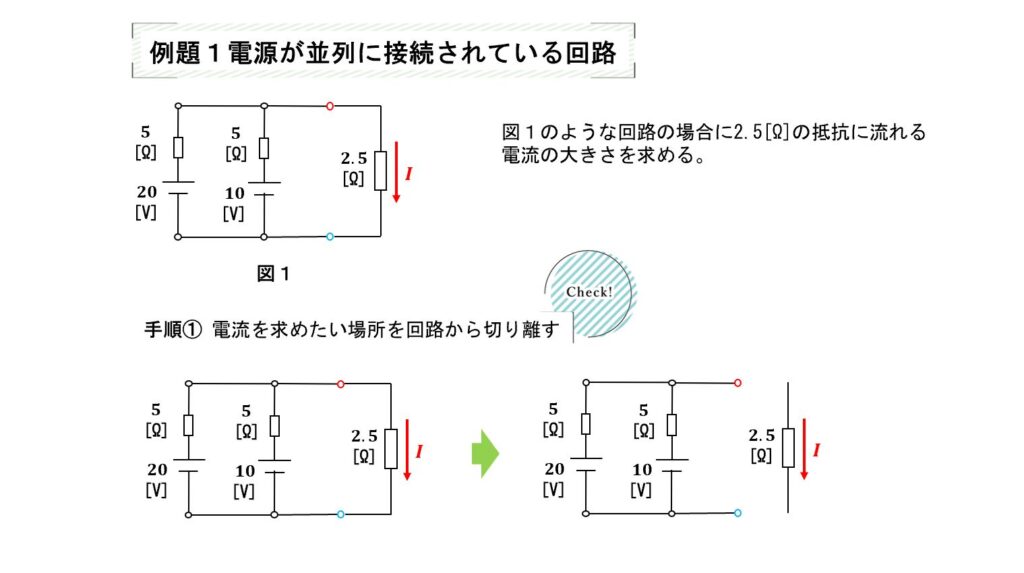
例題1
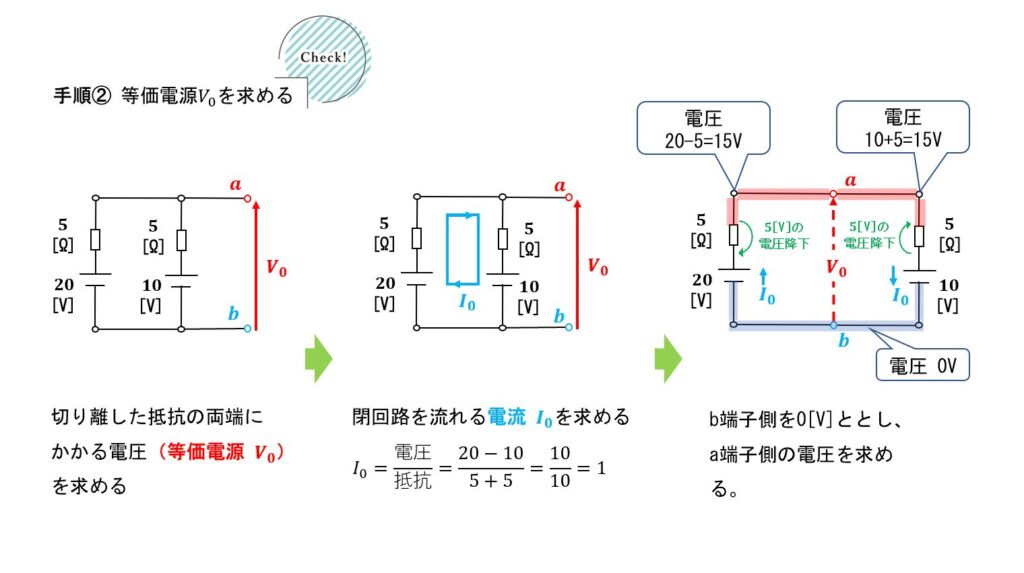
解法手順1-1
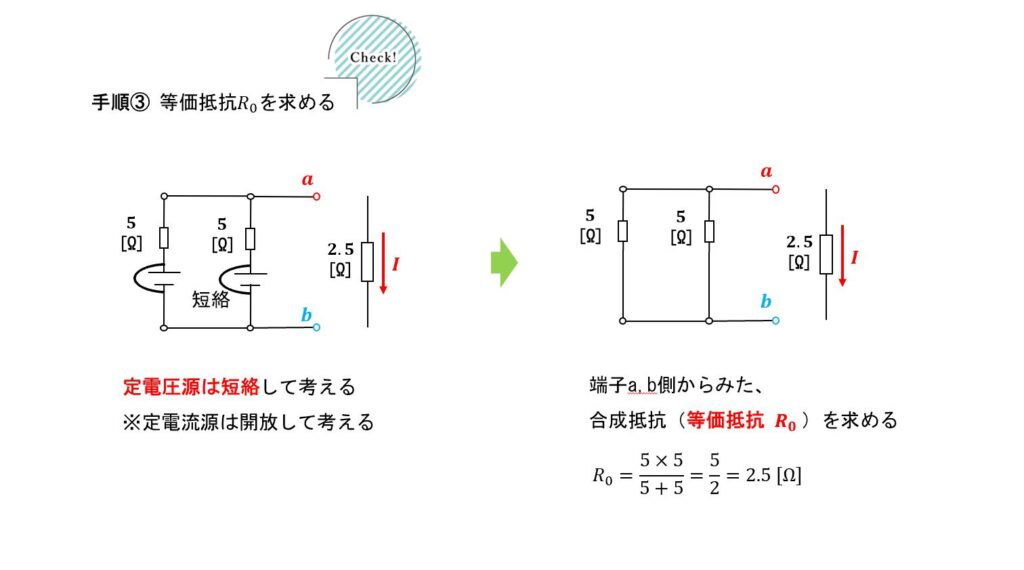
解法手順1-2
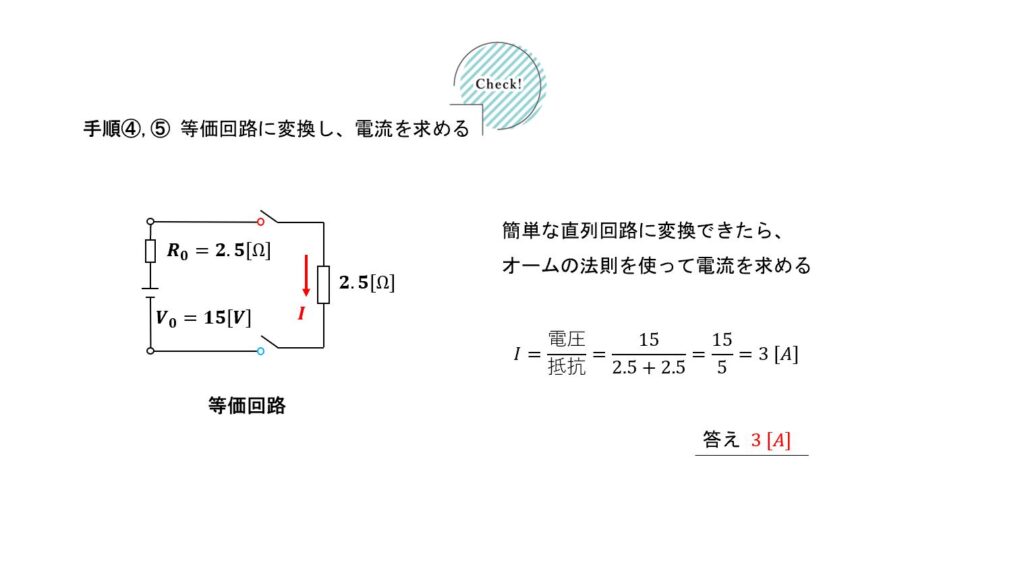
解法手順1-3
例2ブリッジ回路を流れる電流を求める
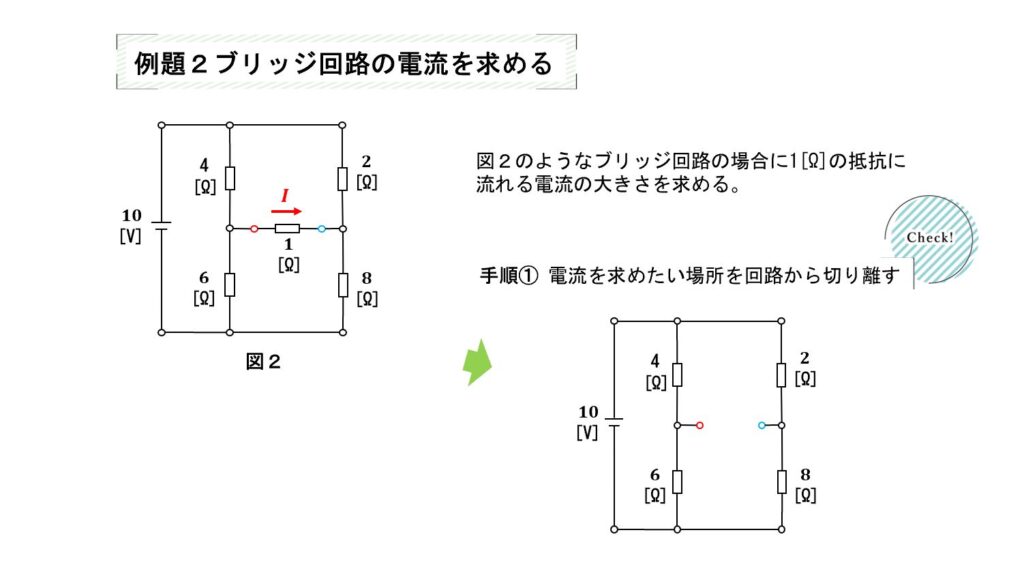
例題2
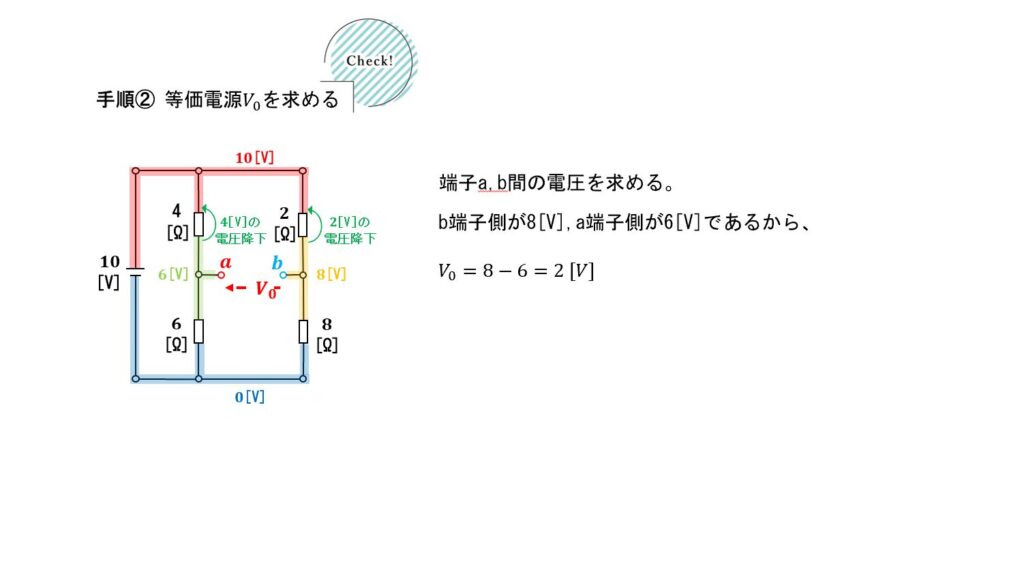
解法手順2-1
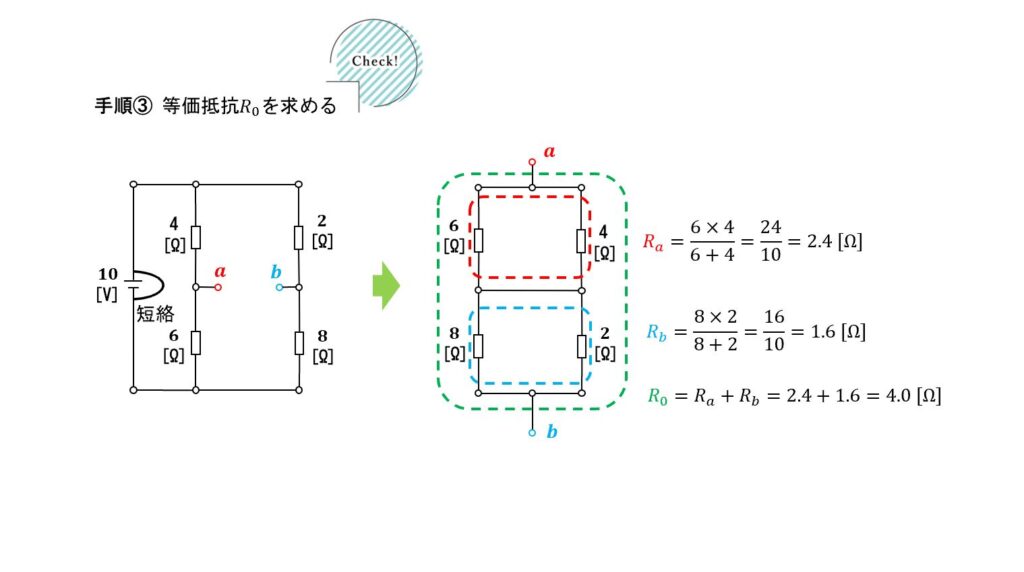
解法手順2-2
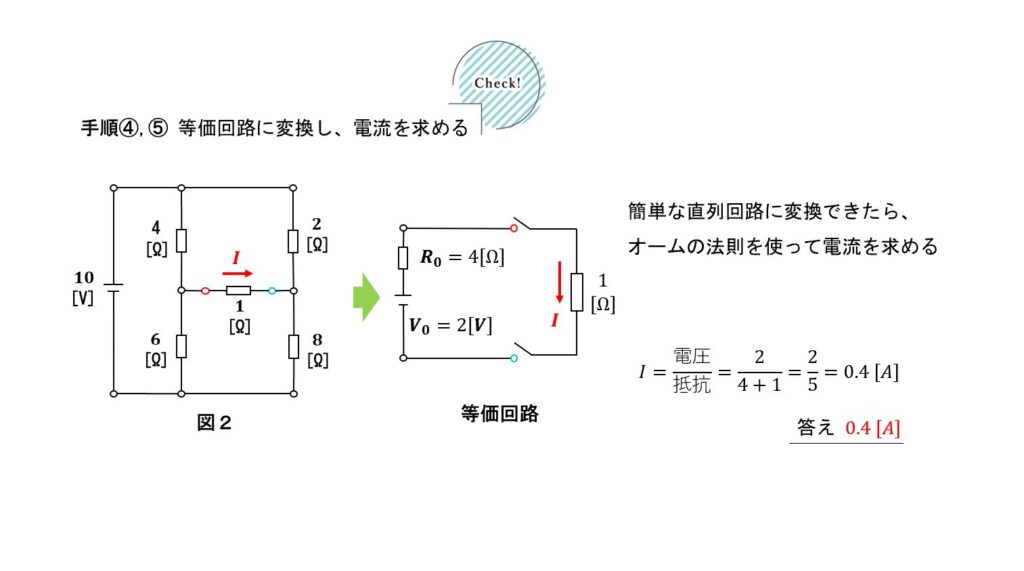
解法手順2-3
例3一線地絡電流を求める
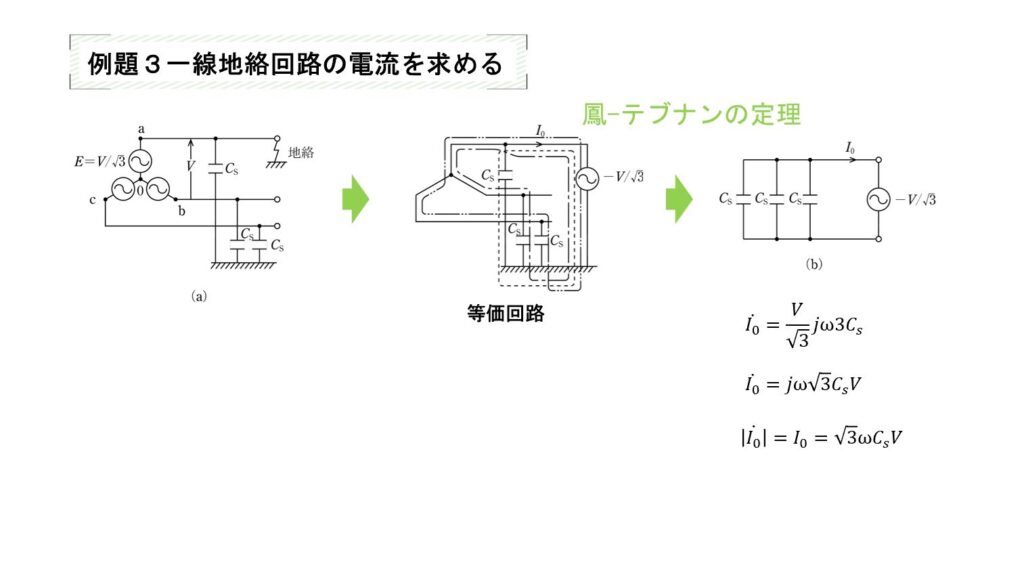
一線地絡電流での利用例
一線地絡電流の計算については、正相、逆相、零相のインピーダンスを考慮しなければいけない場合は、ここで紹介したものよりもさらに複雑になります。
まとめ
まとめ
鳳⁻テブナンの定理は任意の場所を電流を求める場合に有効です。
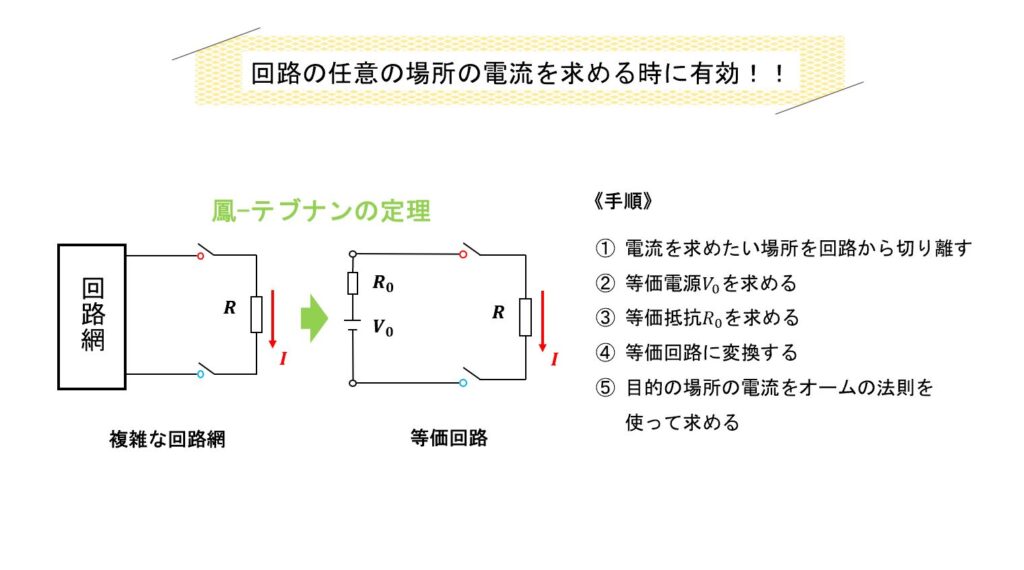
定理の内容は、複雑な回路を内部抵抗をもつ電圧源に変換し簡単な回路にしてしまうという方法。《手法》
① 電流を求めたい場所を回路から切り離す
②等価電源\({}V_0\)を求める
③ 等価抵抗(内部抵抗)\({}R_0\)を求める
④ 等価回路に変換する
⑤ 電流を計算する
定理の内容は、複雑な回路を内部抵抗をもつ電圧源に変換し簡単な回路にしてしまうという方法。《手法》
① 電流を求めたい場所を回路から切り離す
②等価電源\({}V_0\)を求める
③ 等価抵抗(内部抵抗)\({}R_0\)を求める
④ 等価回路に変換する
⑤ 電流を計算する
私も、電験三種を受験していたころは「よくわかんないけど、やり方を覚えておけば使えるからいいや」くらいに思っていました。
二種の勉強するようになり、ようやく鳳-テブナンの定理って特定の場面で、すごく便利だということに気づきました。
導出方法を暗記するだけでも、問題は解けますが理屈をわかっていると自信をもって回答できます。
電験合格を目指して頑張りましょう!!ではまた。






コメント