増幅回路
増幅回路とは、入力信号の振幅を大きくして出力することのできる回路を言います。
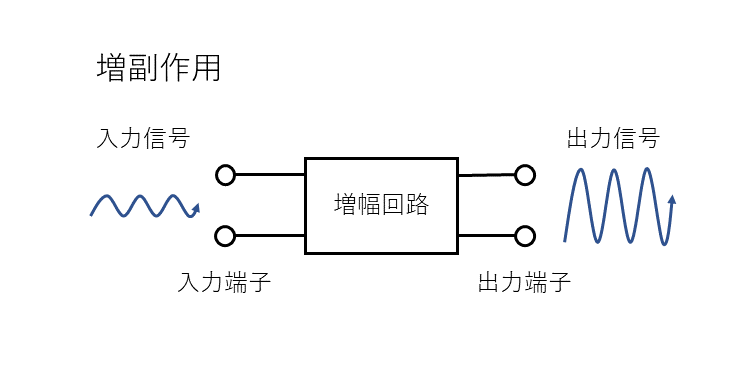
この時、入力信号に対する出力信号の比を増幅度と呼び以下の式で表します。
$$A=\frac{出力信号}{入力信号}$$
また、複数の増幅回路が接続されているときの増幅度は次のように求めます。
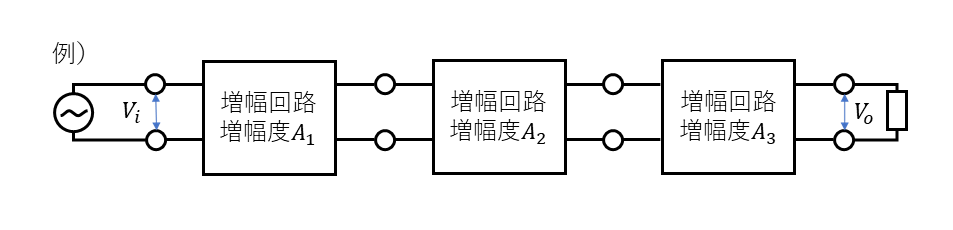
\(A{}_{oll}=A{}_1\times A{}_2\times A{}_3\)
ゲインとは
ゲイン(利得)とは、増幅度を\(\log_{10}\)(常用対数)を使って表したものです。
ゲイン\(G=\log_{10} \left(増幅度A\right)\)
増幅回路が複数ある場合は、増幅度の数値が大きくなり計算が大変になるのでゲインが利用されています。
電験三種で使用されるのは主に次の3つです。
\(G{}_P=10\log_{10}\frac{P{}_{out}}{P{}_{in}}\) [dB]
\(G{}_V=20\log_{10}\frac{V{}_{out}}{V{}_{in}}\) [dB]
\(G{}_I=20\log_{10}\frac{I{}_{out}}{I{}_{in}}\) [dB]
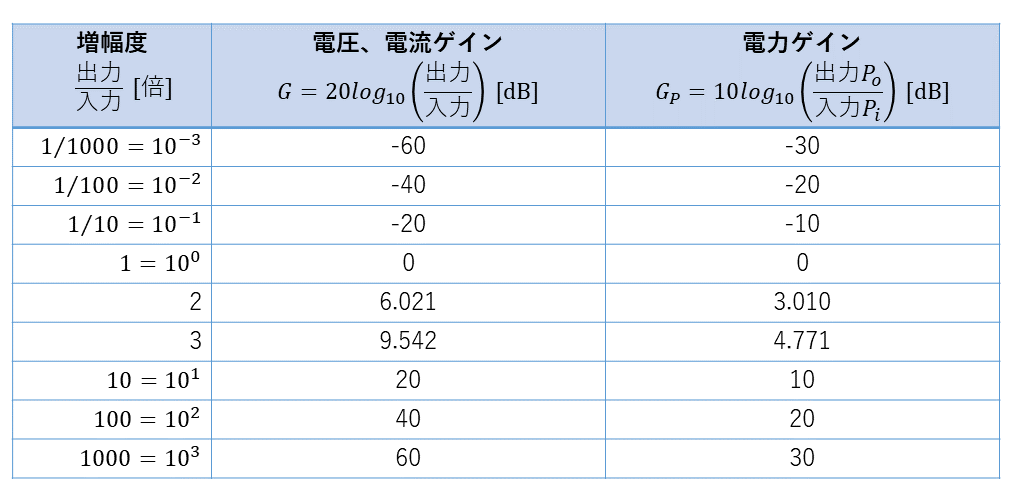

ところで、なんで電力は10でそれ以外は20が付くんだ?
logの前に10や20が付く理由
10が付く理由
単位 [dB]デシベル とは振動のレベルを表すときに使用します。
単位の基準は[B]ベルです。
\(1\) [B]\(=10\) [dB]
なので、\(\log_{10} \)[dB]表記にすると\(\log_{10}\)の前に\(10\)が現れるようになります。
20が付く理由
電圧や電流では、\(\log_{10}\)の前に\(10\)ではなく\(20\)が付いています。
これは、電力が電圧もしくは電流を二乗することで得られる値だからです。
電力のゲインを基準に考えてみましょう。
電力=抵抗\(\times\)電流の二乗
\(P = R\times I{}^2\)
で表されます。これを電力のゲインの式へ代入すると
\(G{}_P=10\log_{10}\frac{P{}_{out}}{P{}_{in}}\)
\(G{}_P=10\log_{10}\frac{RI{}^2{}_{out}}{RI{}^2{}_{in}}\)
\(G{}_P=10\log_{10}\left(\frac{I{}_{out}}{I{}_{in}}\right){}^2\)
\(G{}_P=2\times 10\log_{10}\frac{I{}_{out}}{I{}_{in}}\)
\(G{}_P=20\log_{10}\frac{I{}_{out}}{I{}_{in}}=G{}_I\) [dB]
これで、電力のゲインの式が求めることができました。
電圧でも同様に考えることができます。

理屈が分かってスッキリした!






コメント