同期発電機の端子電圧[V]や出力[kW]を計算する問題を解くうえで、等価回路を理解することは非常に重要です。
また、誘導機の場合と異なりベクトルを用いての出題も多いため電圧・電流の関係を表すベクトル図についてもどのように表してくのかを理解する必要があります。
計算が苦手な方にも理解しやすいように、極力、計算過程や言葉を省略せずに解説していきます。
同期発電機の等価回路
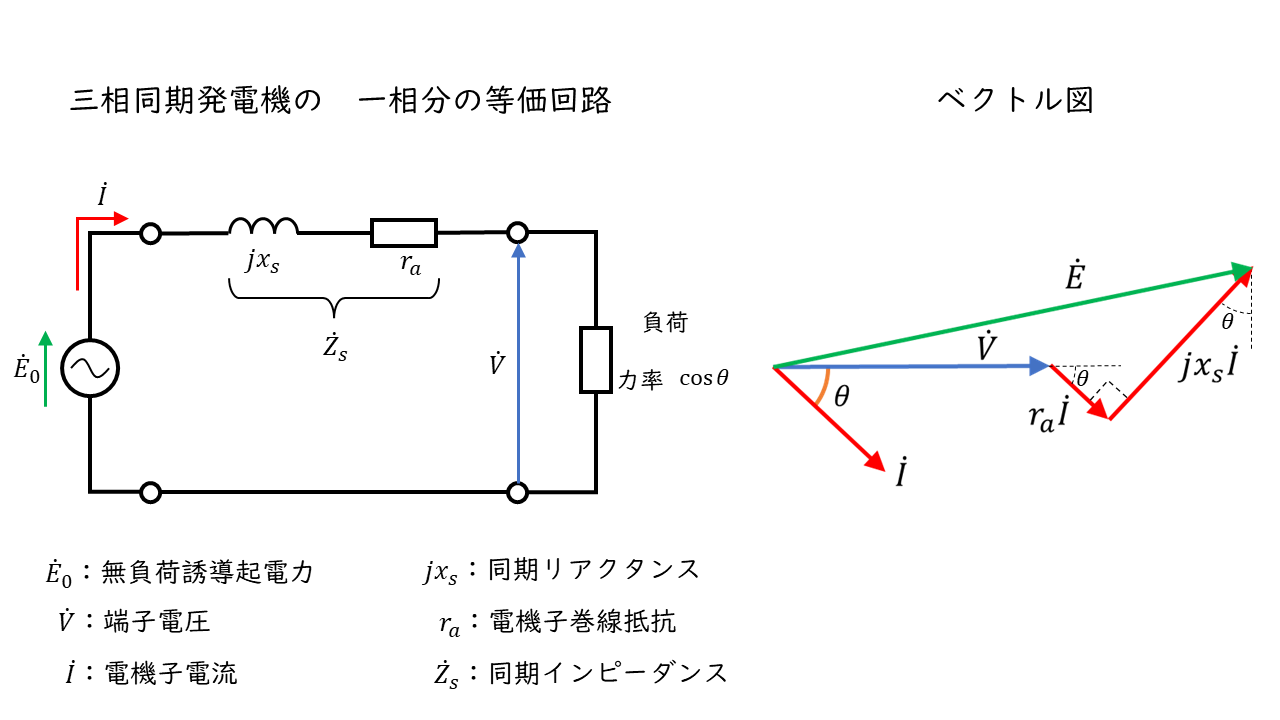
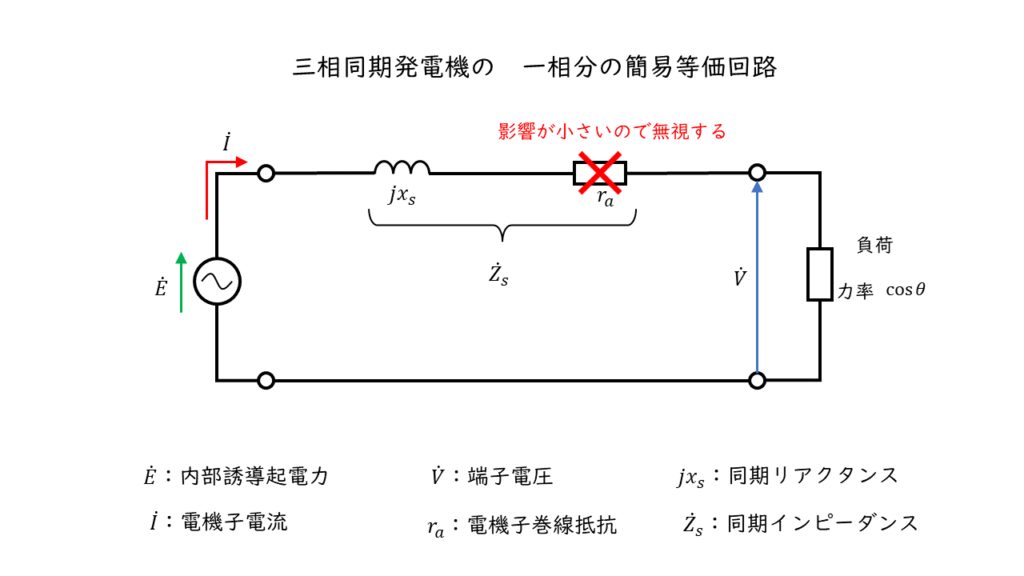
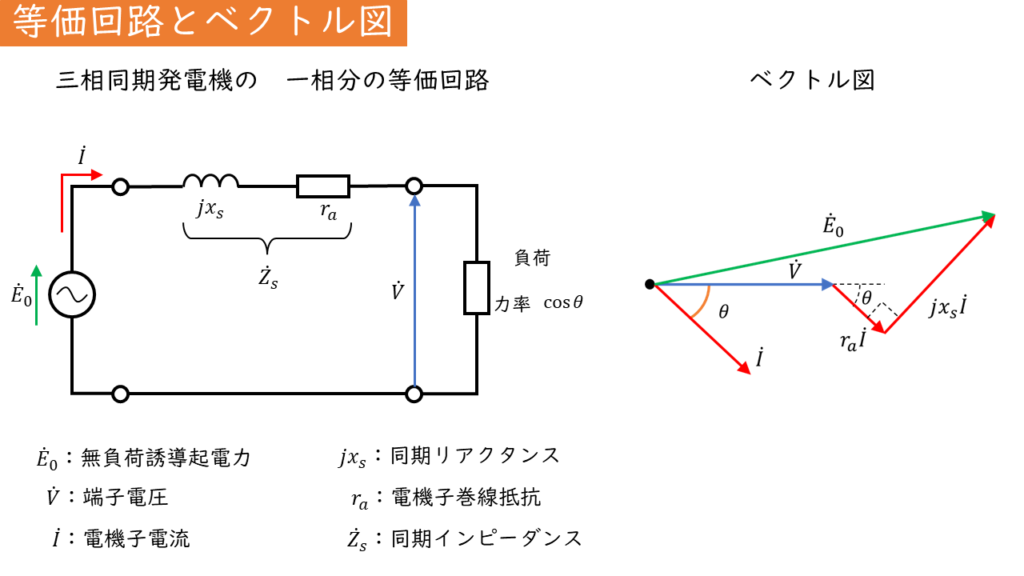
三相同期発電機の一相分の等価回路とベクトル図は、上図のように表されます。
等価回路における電源
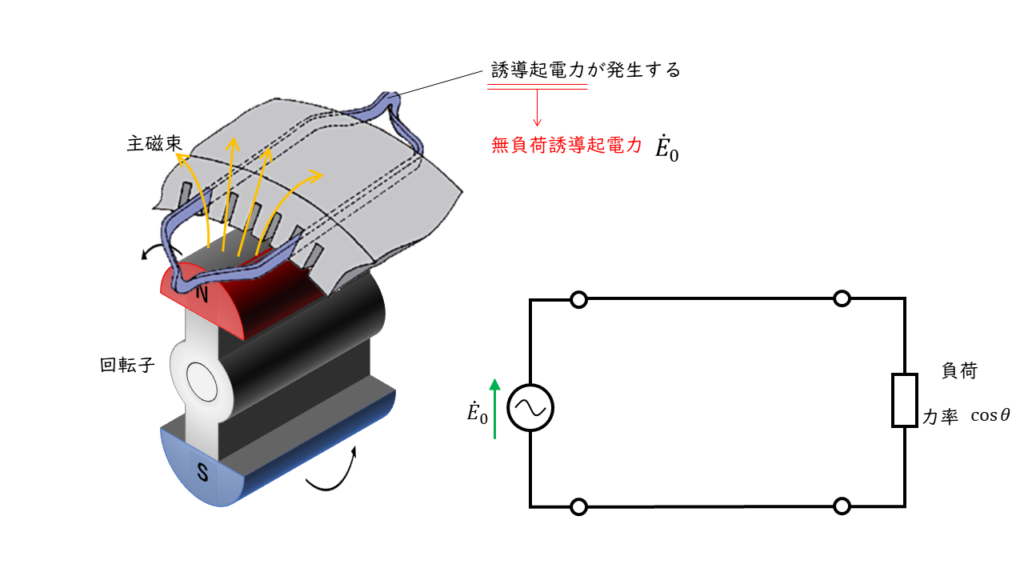
界磁巻線(主磁束)と電機子巻線による電磁誘導が発生します。この時の誘導起電力を\(\dot{E}_0\)[V]とし、等価回路における電源として表します。
この誘導起電力は、負荷の有無にかかわらず、発電機を運転していれば発生するので「無負荷誘導起電力」と呼びます。
等価回路におけるインピーダンス
三相同期発電機の等価回路を書く際には、次の3つを影響を考慮する必要があります。
- 電機子反作用によるリアクタンス
- 漏れリアクタンス
- 電機子巻線の抵抗
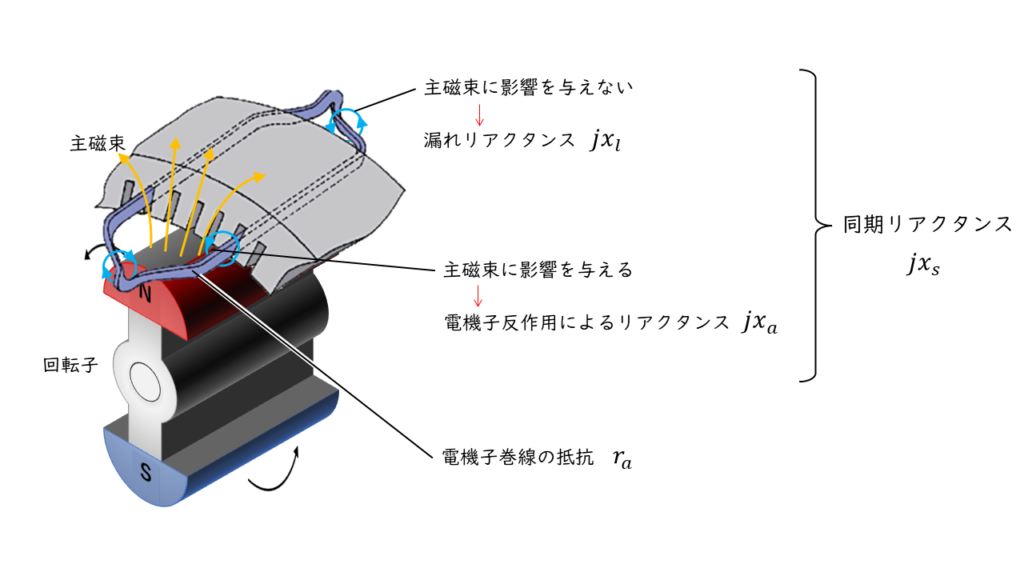
3つの影響を全てまとめたものを同期インピーダンス\(\dot{Z}_s\)[\(\Omega\)]と呼びます。
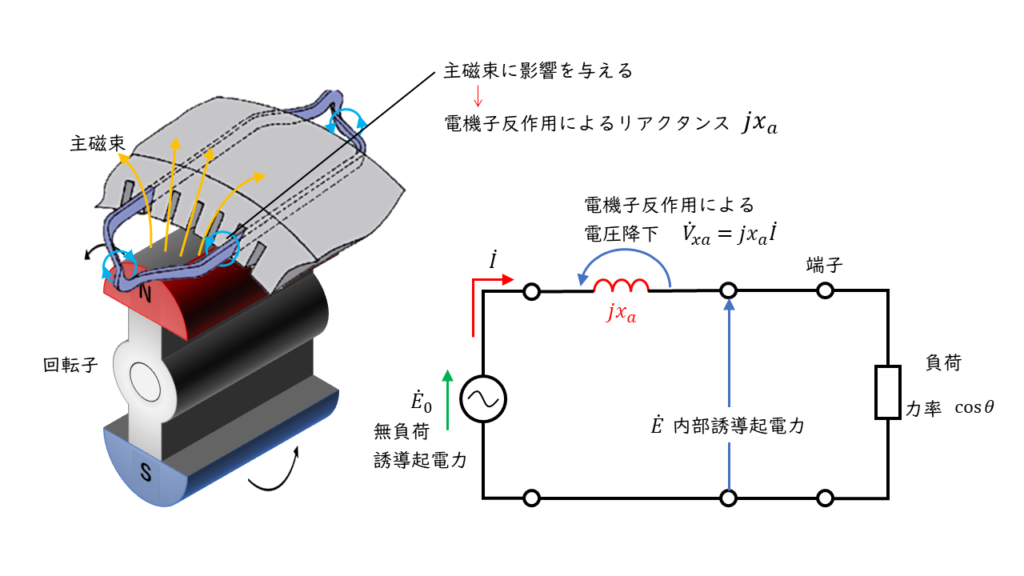
電機子反作用によるリアクタンス
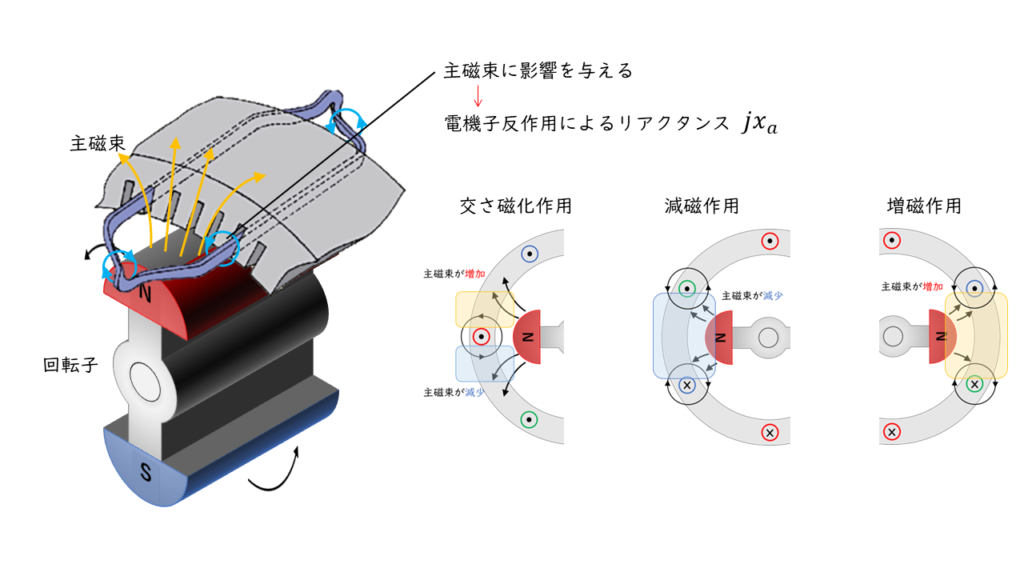
電機子反作用が発生すると、主磁束(界磁巻線が発生させる磁束)は増減するため、電機子巻線で発生する起電力も増減します。
この起電力の増減を電機子巻線のリアクタンス\(x_a\)[\(\Omega\)]によって生じる電圧降下と解釈して考えます。
負荷の影響によって電気子反作用は増磁作用、減磁作用など変化します。
そのため、発電機の内部で発生する電圧は、発電機運転中は常に発生する無負荷誘導起電力と電気子反作用のリアクタンスによる電圧降下を考慮しなければいけません。
無負荷誘導起電力から、電気子反作用のリアクタンスによる電圧降下を引いた値を「内部誘導起電力」\(\dot{E}\)[V]といいます。
漏れリアクタンス
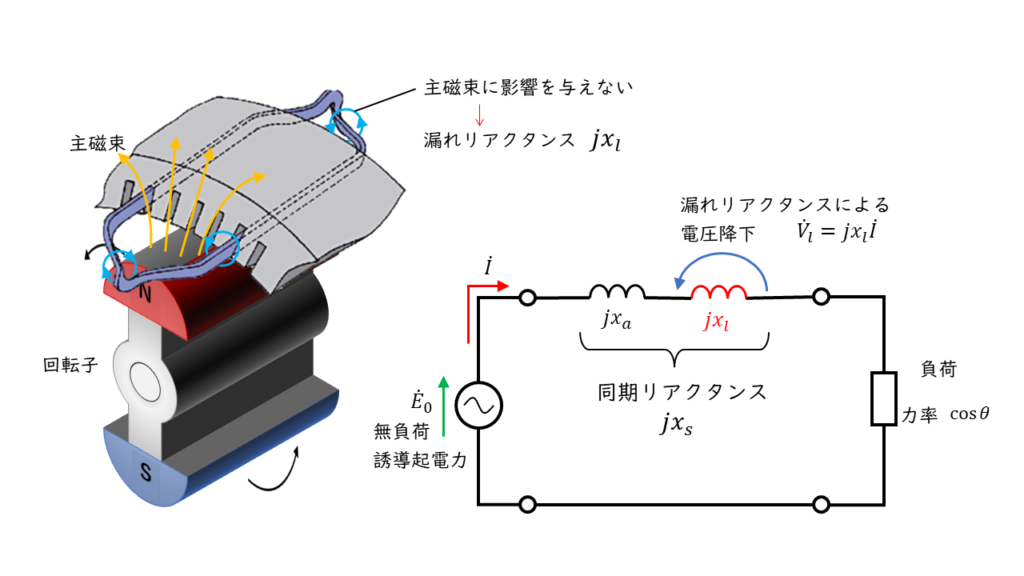
電機子巻線の周りに発生する磁束のうち主磁束に影響を与えない磁束を漏れ磁束\(\phi _l\)と呼んでいます。漏れ磁束\(\phi _l\)は、電機子巻線と鎖交するだけですが、大きさが変化するとコイルの磁束の変化を嫌う性質が働くため、誘導起電力に電圧降下が発生します。
この電圧降下を発生させるものを漏れリアクタンス\(x_l\)[\(\Omega\)]と解釈します。
また、漏れリアクタンスと電気子反作用によるリアクタンスを合わせて同期リアクタンス\(x_s\)[\(\Omega\)]と呼びます。
電機子巻線抵抗
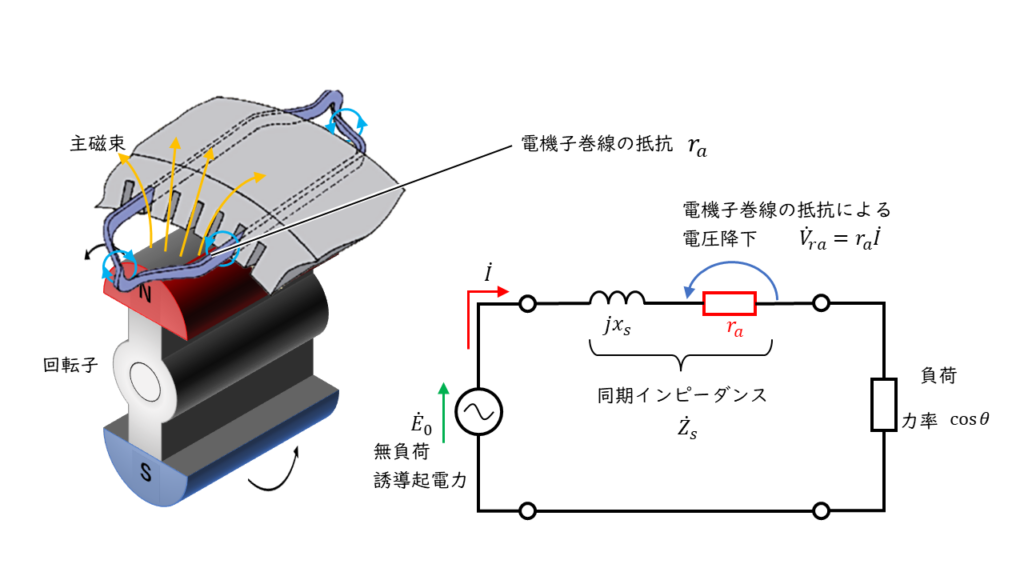
電機子巻線は、回転子鉄心に巻き付けられている導体です。導体には、電気抵抗が存在すため、これを電機子巻線抵抗\(r_a\)[\(\Omega\)]と呼びます。
同期発電機のベクトル図
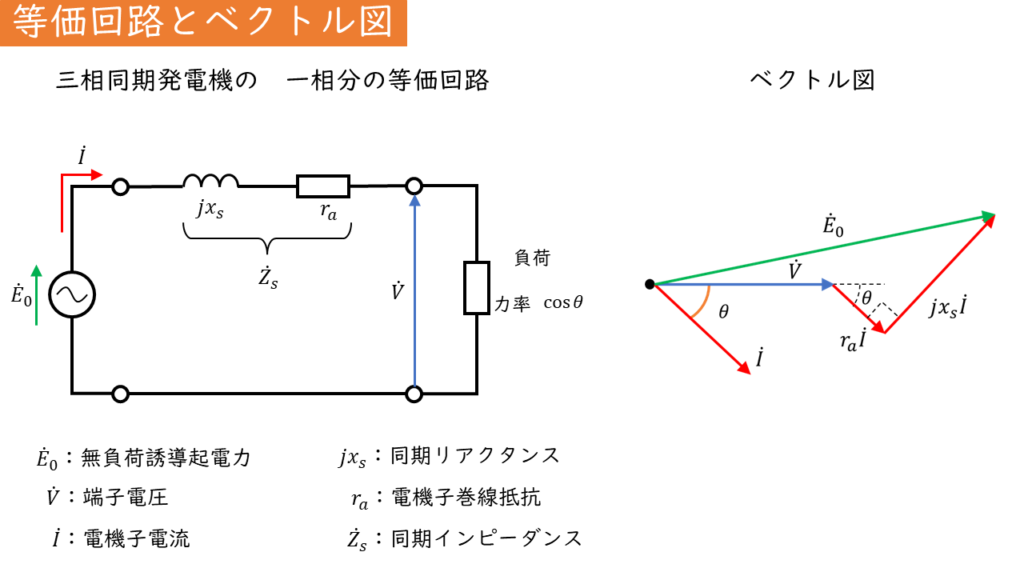
同期発電機の回路図をもとに電流、電圧を関係を表すベクトル図を書いていきます。
無負荷誘導起電力\(\dot{E}_0\)[V]、同期リアクタンス\(x_s\)[\(\omega\)]、電機子巻線抵抗\(r_a\)[\(\Omega\)]、端子電圧\(\dot{V}\)[V]、電機子巻線を流れる電流\(\dot{I}\)[A]、力率角\(\theta\)[rad]で表すことにします。
無負荷誘導起電力、電機子巻線を流れる電流を書く
一般的に、端子電圧を基準のベクトルとして考えることが多いです。
今回も端子電圧を基準ベクトルとしてベクトル図を作成していきます。
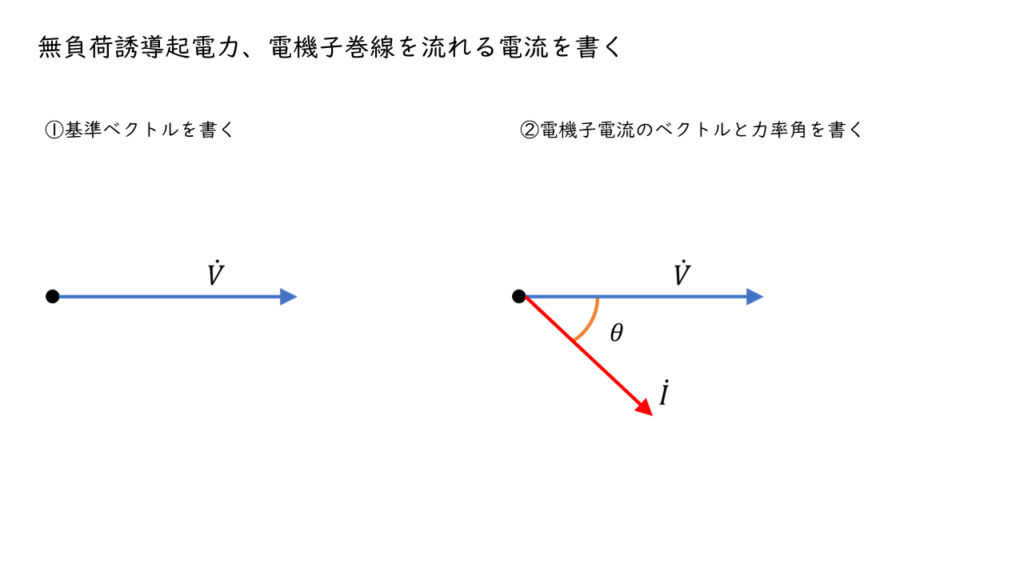
電機子巻線抵抗及び同期リアクタンスによる電圧降下を書く
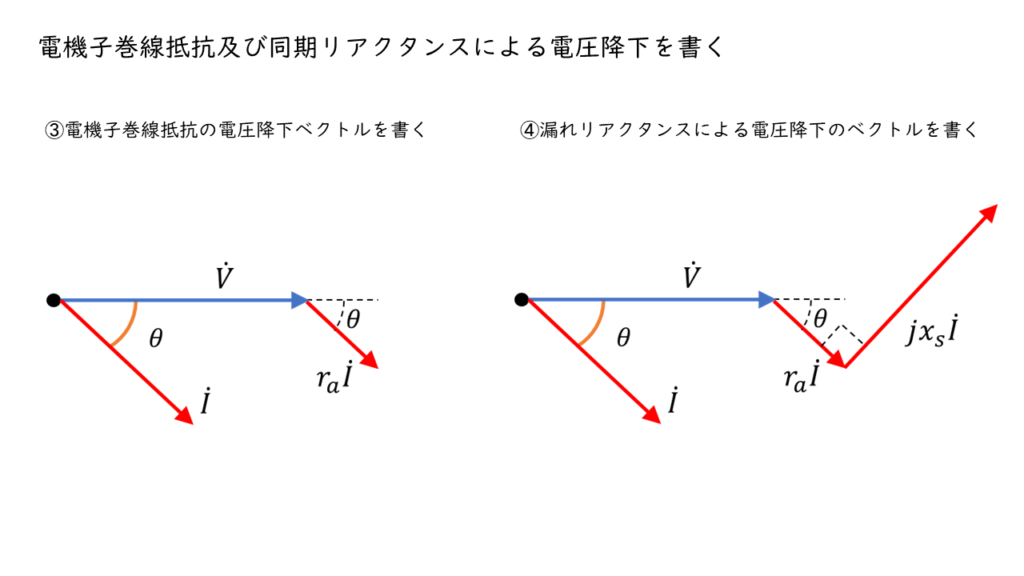
回路図より電機子巻線と同期リアクタンスを流れる電流は、どちらの場合も\(\dot{I}\)[A]です。よって、それぞれの電圧降下は以下のようになります。
電機子巻線抵抗の電圧降下:\( \dot{V}_a = r_a \times \dot{I} \) [V]
同期リアクタンスの電圧降下:\( \dot{V}_s = j x_s \times \dot{I} \) [V]
抵抗を流れる電流はとリアクタンス(コイル)を流れる電流の位相は90度ずれているため、ベクトル図で表す場合には垂直になるように書き表します。
無負荷誘導起電力のベクトルを書く
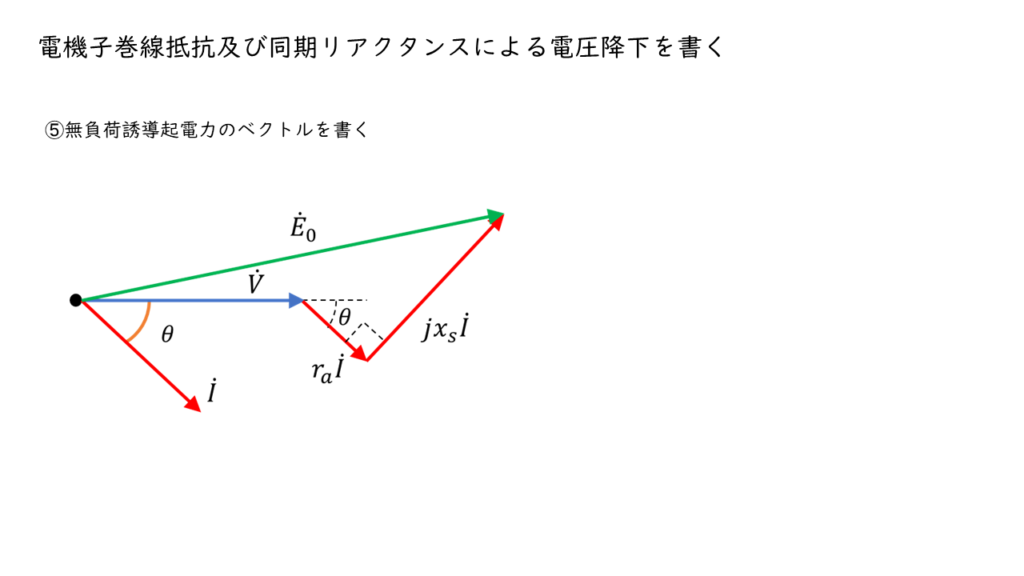
以上が同期発電機における1相分のベクトル図を作図する手順です。
同期発電機の出力計算
同期発電機において、一般的に同期リアクタンス\(x_s\)[\( \Omega\)]は電機子巻線抵抗\(r_a\)[\(\Omega\)]よりもかなり大きな値となります。
そのため試験問題では、電機子巻線抵抗を無視して計算する場合が多いです。
三相同期発電機の内部起電力\(\dot{E}\)[V]、端子電圧\(\dot{V}\)[V]、電機子電流\(\dot{I}\)[A]、同期リアクタンス\(x_s\)[\(\Omega\)]、負荷力率\(\cos \theta\)と表すことにします。
電圧と電流、インピーダンスの関係を式に表すと以下のようになります。
(キルヒホッフの電圧則より)
\( \dot{E} = jx_s \dot{I} + \dot{V} \) [V]
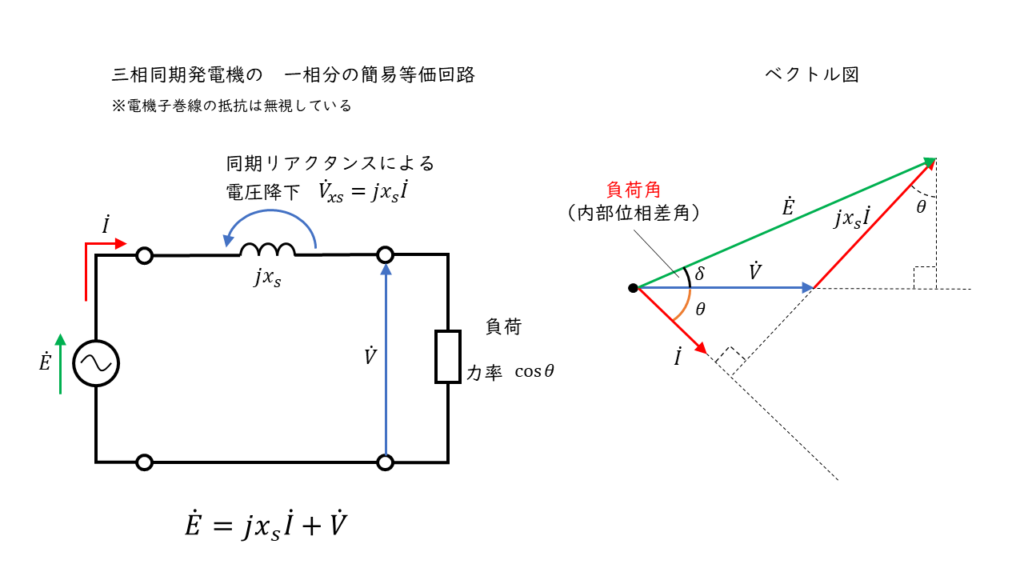
内部誘導起電力と端子電圧の位相差(2つのベクトルが作る間の角)を負荷角(内部位相差角)といい、\( \delta\)(デルタ)で表します。
発電機の出力は、端子電圧\(\dot{V}\)[V]と電機子電流\(\dot{I}\)[A]、力率角\(\cos \theta\)の積で求めることができます。
一相分の出力:\( P_1 = V \times I \cos \theta \approx \displaystyle \frac{VE}{x_s} \sin \delta \) [W]
三相分の出力:\( P_3 = 3 \times P_1 \approx \displaystyle \frac{3VE}{x_s}\sin \delta \) [W]
同期発電機の出力\( P_1 = VI\cos \theta\)をどのようにすれば、\( \displaystyle \frac{VE}{x_s}\sin \delta \)と置き換えることができるのでしょうか。
2つの式の変形は、ベクトル図を用いて考えることができます。
※ただし、電機子巻線抵抗を無視したベクトル図を用います。
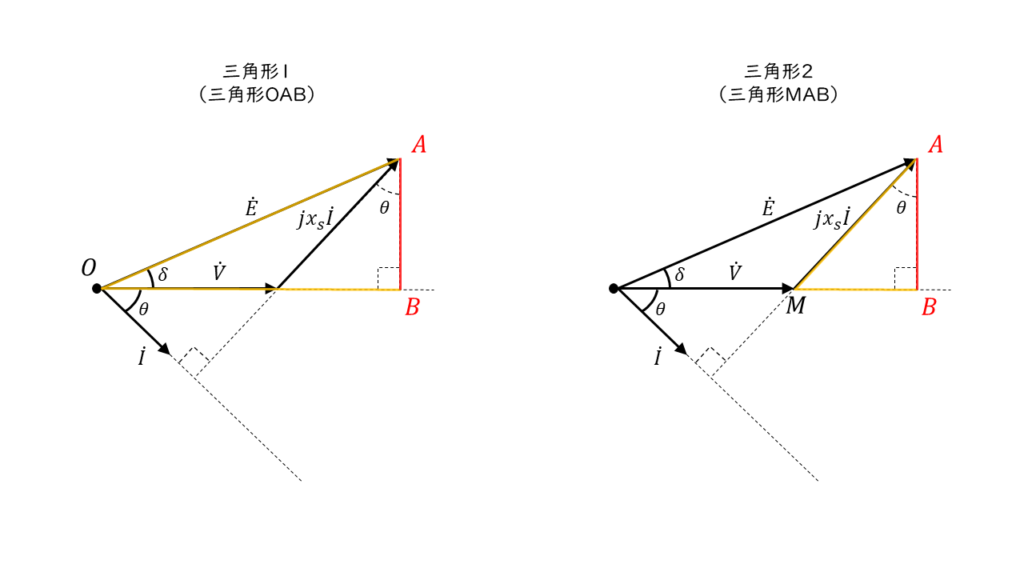
三角形1の辺ABに注目すると、\(辺AB = E \sin \delta \)…①
三角性2の辺ABに注目すると、\(辺AB = x_s I \cos \theta \)…②
①と②は同じ辺ABを表した式なので、
\( E \sin \delta = x_s I \cos \theta \)…➂
となります。式➂の関係を利用して、同期発電機の出力\( P_1 = VI\cos \theta\)を変形していきます。
\( \begin{align} P_1 &= VI \cos \theta \\ &= V \times \displaystyle \frac{E}{x_s} \sin \delta \\ &= \displaystyle \frac{VE}{x_s} \sin \delta \end{align} \)
以上のようにして公式を導くことができます。
三相分の公式については、一相分の式を3倍するだけで求めることができます。
試験問題には、「損失は無視するものとする」あるいは「電機子巻線抵抗は無視するものとする」と記載されている場合があります。
上記の2つはどちらも同じ意味として使用されています。問題文の一番最後に書かれることが多いため、注意しておきましょう。
三相同期発電機の並行運転
最後に、三相同期発電機の並行運転について解説します。
並行運転(並列運転)とは、複数台の発電機を同じ母線(導体)に並列接続して、共通の負荷に電力を供給することを言います。
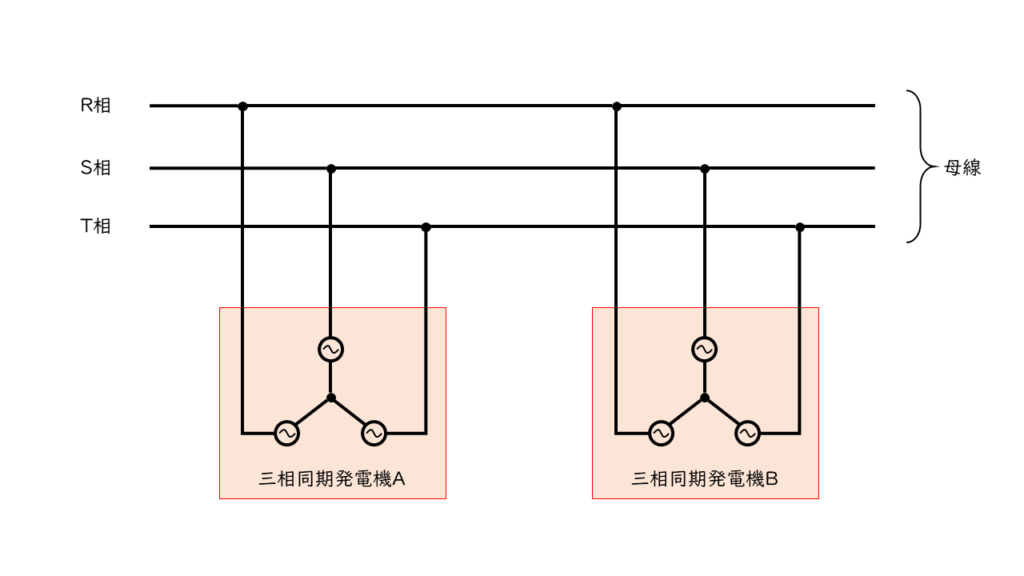
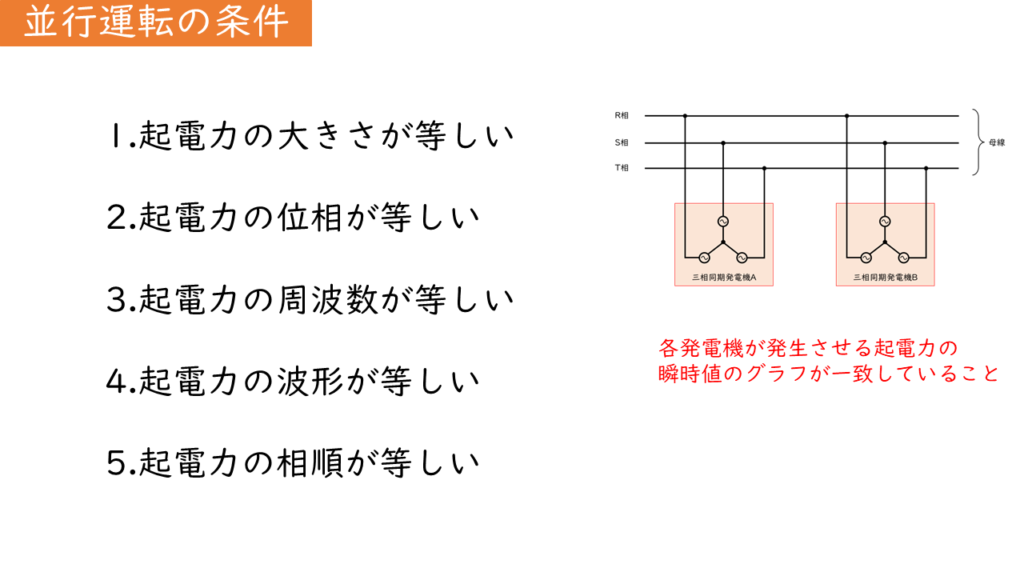
並列運転を行うためには、以下の条件を満たす必要があります。
- 起電力の大きさが等しいこと
- 位相が一致していること
- 周波数が等しいこと
- 波形が等しいこと
- 相順が等しいこと
起電力の大きさについては、界磁電流を制御することで主磁束の大きさが変化するため、起電力の大きさも変化します。
位相、周波数については、回転速度を制御することで調整が可能です。位相の確認には、「同期検定器」を使用します。
まとめ

過去の出題実績
H16年度 問6
H20年度 問5
H22年度 問15
H23年度 問4
H28年度 問15
H30年度 問6
R元年度 問15
R4年度上期 問4








コメント