静電気分野の出題はコンデンサが中心になります。コンデンサに関する問題は、公式と解き方さえ覚えることができれば解答を導くことができます。しかし、コンデンサを正しく理解するためには電位やクーロン力といった内容の理解も必要になります。静電気は電験三種において頻出のテーマですから、合格するために得点源にしておきたい内容です。
- 電位、電界、静電力の違いを理解する
- 電気力線と電束の違いを理解する
- コンデンサに蓄えられる電荷と電界、電圧の関係を理解する
- 静電容量と静電エネルギーの計算ができる
電位、電界、クーロン力の違い
点電荷の作る電位、電界と2つの点電荷の間に働く静電力(クーロン力、静電気力)の公式は非常に似通ったものです。
電位 : \( \displaystyle V = \frac{Q}{4 \pi ε r} \rm [V] \)
電界 : \( \displaystyle E = \frac{Q}{4 \pi ε r^2} \rm [V/m] \)
静電力 : \( \displaystyle F = \frac{Q_1 \ Q_2}{4 \pi ε r^2} \rm [N] \)
公式が似ているということは、電位、電界、クーロン力はとても関連性が高いということです。試験本番で、公式を間違って使いことがないようにどういった意味を持つ式なのか整理しておきましょう。
電位とは
電気的な位置(高さ)を表すものです。一般に、地面(大地)を基準の0[V]として考えます。電気は水と同じで高い場所から低い場所へ向かって流れます。そのため、電位に差がない場所では自然に電気が流れることはありません。
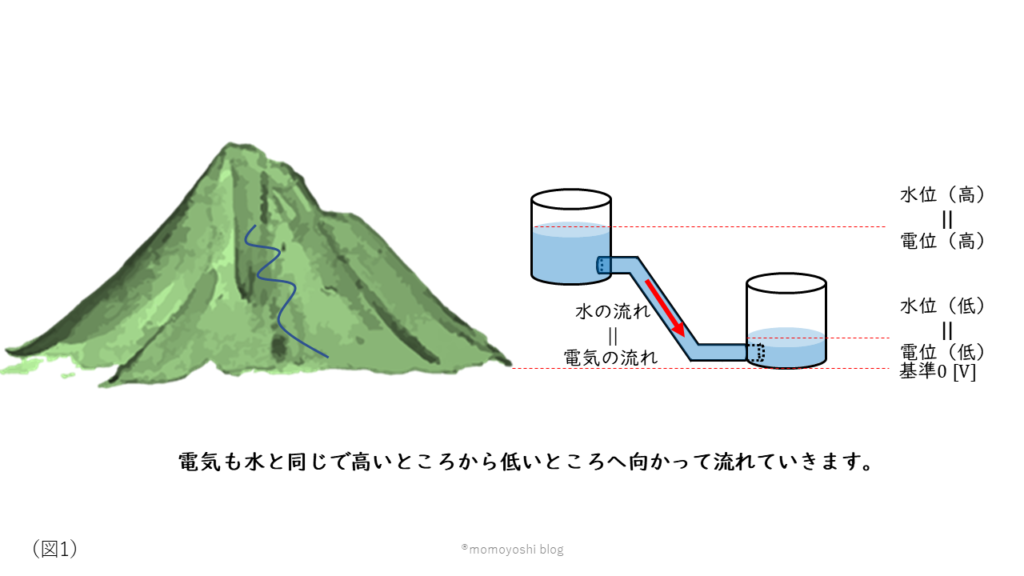
電位の差が同じであっても、落差の傾き具合には違いがあります。この電位差の傾き具合の大きさを表すのが電界(電場)です。電位差の傾きが多きほど電荷を移動させるときに必要なエネルギーが大きくなります。
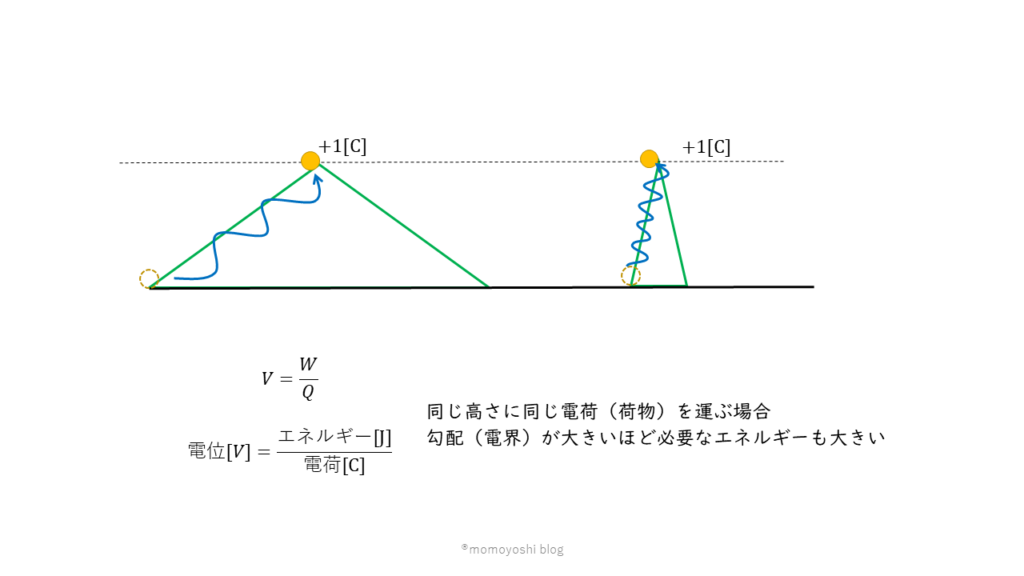
電界とは
電荷の周囲には電気的な力(静電力、クーロン力)が働く空間があります。この静電力のはたらく空間を電界と呼びます。電荷から離れるほど電界は弱くなっていきます。
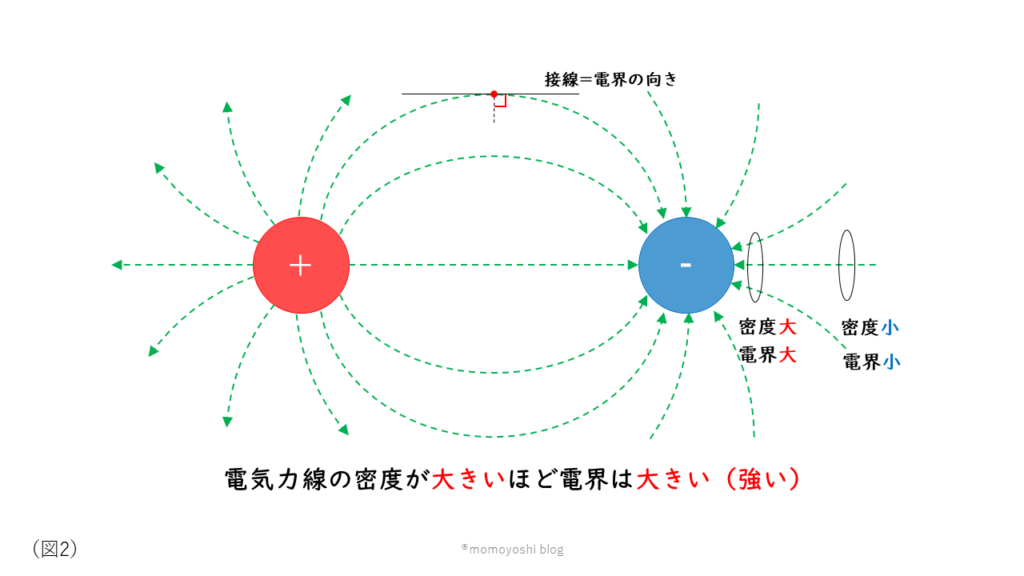
電界は力の働く空間を表すものであるため、大きさだけでなく向きも重要です。目で見ることのできない電界の様子は、矢印を使って表します。この電界の様子を表す矢印のことを電気力線と呼びます。電気力線の矢印は電界の向き、密度(密集度合い)は電界の大きさを表します。
静電力とは
電界中で電気を帯びた物体に働く力のことです。磁石と同じように、同符号(+同士、ー同士)では反発力、異符号(+とー)では引き付けあう(吸引)力が働きます。
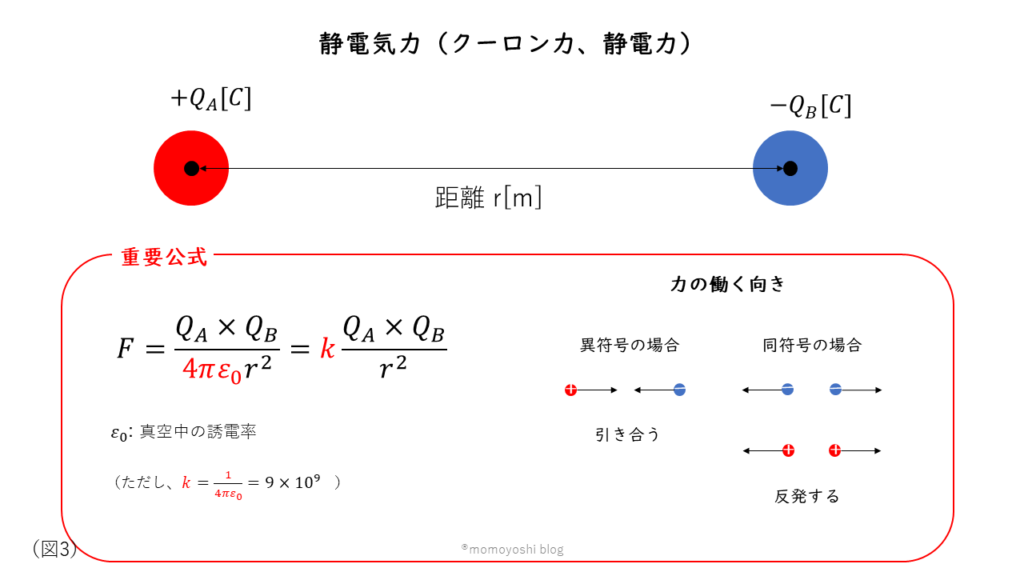
電験三種では、物体の大きさを無視した点(点電荷)が2つもしくは3つある場合での静電力に関する問題がほとんどです。点電荷のまわりには電界が存在するため、2つの点電荷の間に生じる力として参考書で紹介されることが多いです。
電気力線と電束の違いを理解する
静電気分野の本題であるコンデンサの学習に入る前に、電束という言葉を覚えておきましょう。コンデンサの問題を解くうえで、電気力線しか知らないと非常に苦労する場面が多いです。電気力線と電束の違いは図4に示す内容です。
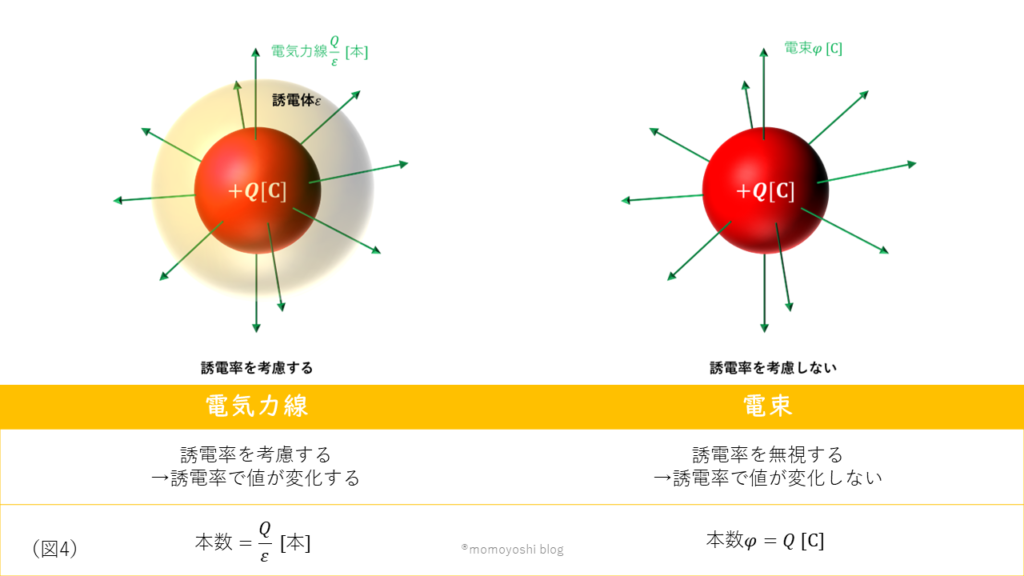
コンデンサに関する問題では誘電率\(ε\)の値を変化させる問が多く出題されてます。そのため誘電率の影響を受ける電気力線では計算が複雑になり、解答時間が足りなくなってしまいます。解答時間の短縮、計算ミス削減のためにも電束の理解は必須といえるでしょう。
コンデンサに蓄えられる電荷と電界、電圧の関係理解する
コンデンサの基礎となる、極板に蓄えられる電荷、極板間の電界、電圧の関係を整理していきましょう。
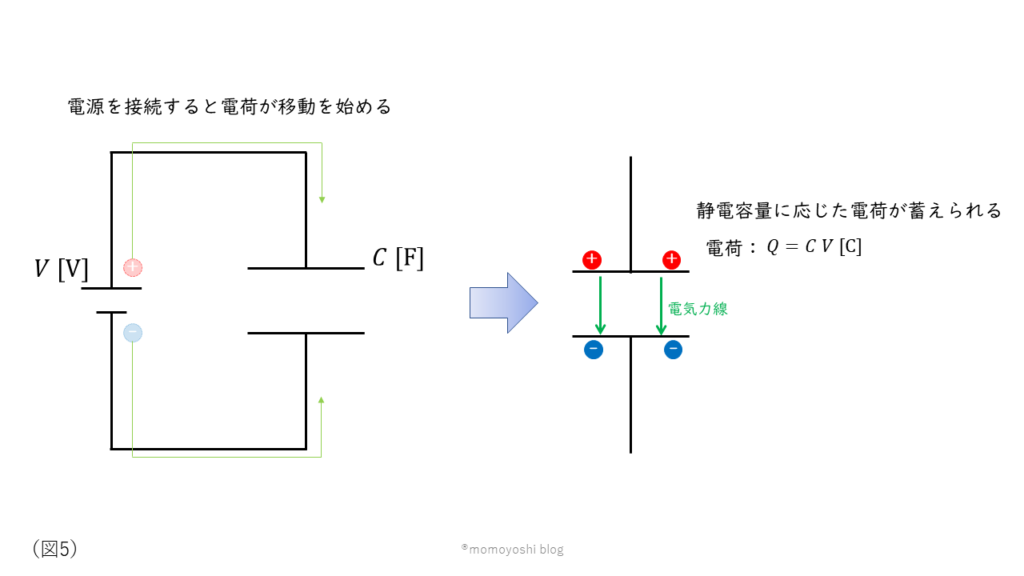
図5に示すようにコンデンサの両端に電圧を加えることで、金属極板に電荷が蓄えられていき、コンデンサの内部に電界が発生していきます。コンデンサに蓄えることができる電荷の量(静電容量)は極板の大きさ(面積)と極板間の距離、極板間の誘電率で決定されます。
静電容量: \( C = μ \displaystyle \frac{S}{d} \rm [F] \)
蓄えられる電荷: \( Q = C \times V \rm [C] \)
平行平板コンデンサの場合、極板上に蓄えられる電荷は均一に分布しているため、内部の電気力線の密度も均一になります。※注1
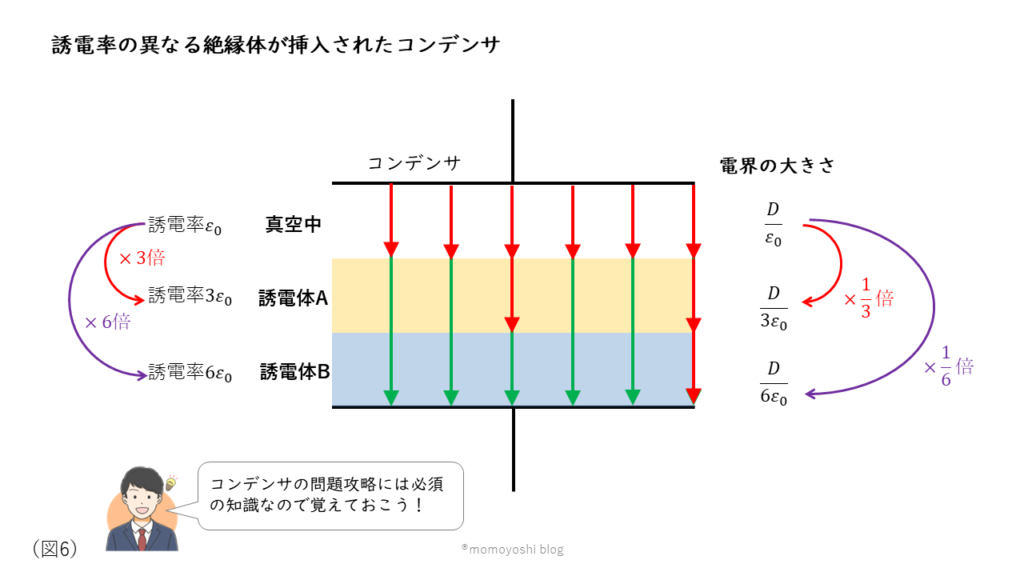
この時にコンデンサ内部に生じる電界の大きさは次の式で表すことができます。
平行平板電コンデンサの電界の大きさ: \( E = \displaystyle \frac{V}{d} \rm [V/m] \)
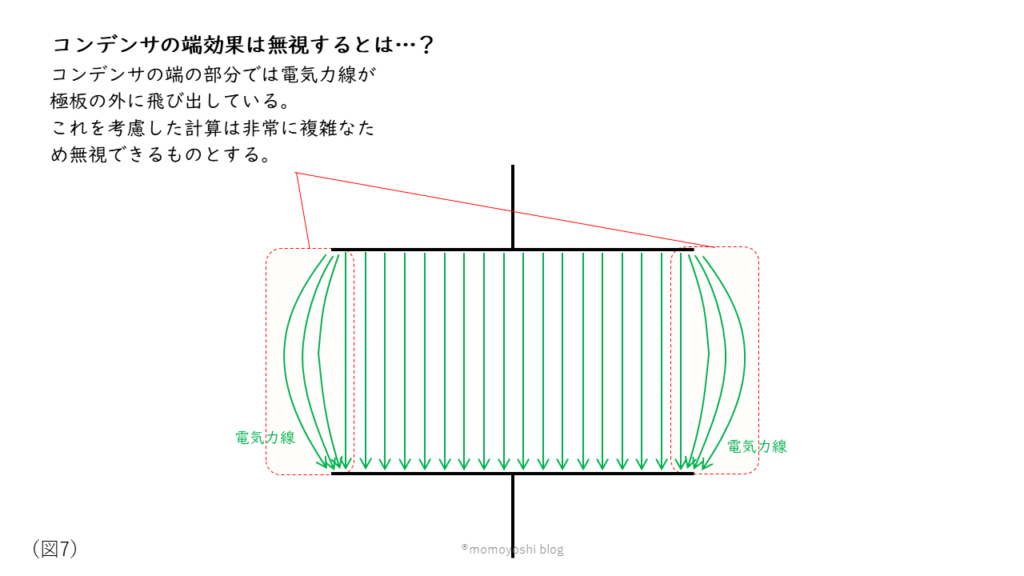
コンデンサ内部の電界は、平等電界(どの点でも同じ大きさの電界)(図7)になります。電験の試験問題では、計算を複雑にしないために「コンデンサの端効果は無視してよい」と記載されています。
電圧、静電容量、電荷などコンデンサの計算ができる
コンデンサに関する実際の試験問題は、1つの公式に当てはめれば答えが導き出せる単純な問題ばかりではありません。複数の公式を組み合わせて利用し計算していくことも必要です。
まずは基本となるコンデンサの公式を覚えていきましょう!
コンデンサの直列つなぎ、並列つなぎ
コンデンサを直列に接続した場合の計算方法は抵抗を並列つなぎにした場合の計算方法と同じになります。
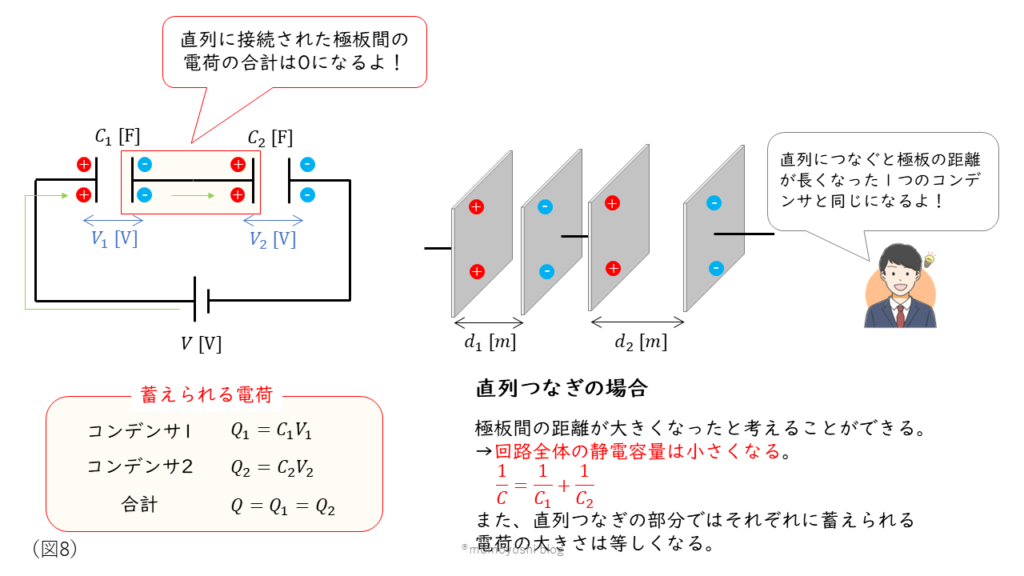
回路全体の静電容量:\( \displaystyle \frac{1}{C} = \displaystyle \frac{1}{C_1} + \displaystyle \frac{1}{C_2} \rm [C] \)
一方、コンデンサを並列つなぎにした場合には、抵抗を直列つなぎにしたときと同じ計算方法になります。
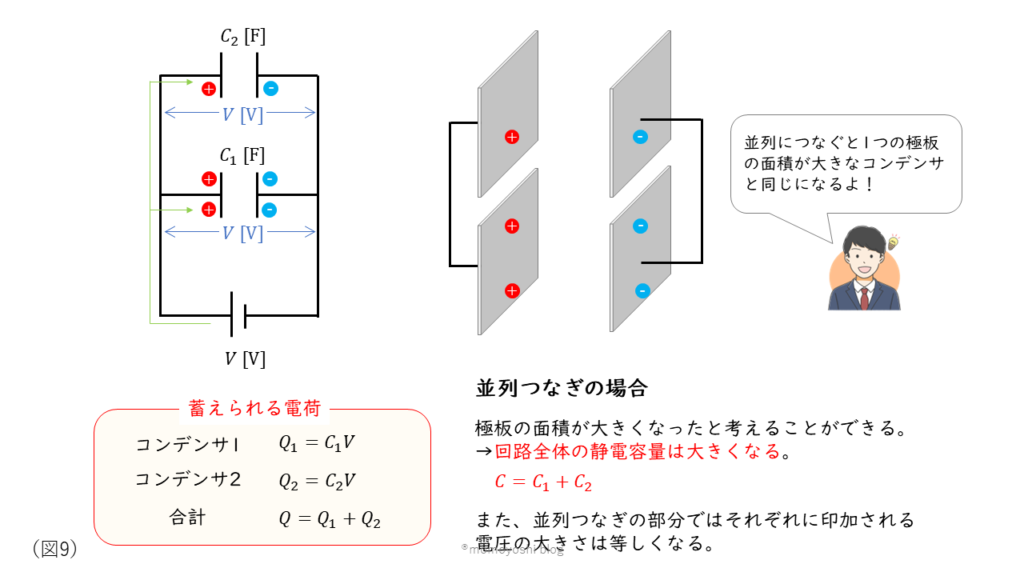
回路全体の静電容量:\( C = C_1 + C_2 \rm [C] \)
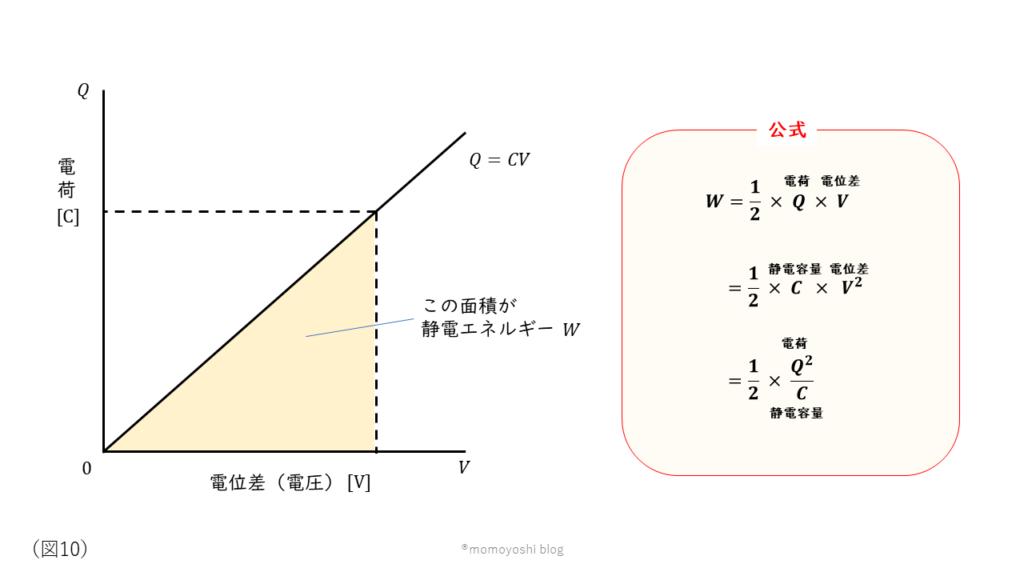
静電エネルギーの計算
静電エネルギーとは充電されたコンデンサがもつエネルギーのことです。静電容量\( C \rm [F] \)のコンデンサに\( Q \rm [C] \)の電荷が蓄えられており、極板間の電位差が\( V \rm [V] \)のとき、静電エネルギー\( W \rm [J] \)は以下の様に表されます。
静電エネルギー:\( W = \displaystyle \frac{1}{2} QV = \displaystyle \frac{1}{2} CV^2 = \displaystyle \frac{1}{2} \displaystyle \frac{Q^2}{C} \rm [J] \)
最後に…
今回は静電気分野攻略のために重要なポイントを紹介しましたが、本ページだけでは不足していると感じる部分もあるかと思います。当ブログでは、より詳細な解説も行っていますので、気になる箇所は関連記事を参考ください。
初めは大変かもしれませんが、コツコツ学習を積み重ねていくことが合格への最短ルートです。
合格に向けてがんばろう!




コメント