電験三種の試験では、三相同期電動機の出力とトルクに関する問題、始動方法に関する問題が過去に出題されており、今のところ問題内容の傾向に変化はないようです。従来はそれほど出題頻度が高くない印象でしたが、令和にはいいてからの試験では、毎年出題されています。
今回は、三相同期電動機の原理~出力・トルクの計算、特性までを豊富なイラストを用いて、徹底解説していきます。
三相同期電動機と三相同期発電機の基本的な構造は同じため、同期発電機の学習がまだの方は、初めに同期発電機の学習を終えることをお勧めします。
それでは、学習を始めていきましょう。
三相同期電動機の原理
三相同期電動機の固定子に三相交流電流を流すと回転磁界を作ることができます。また、回転子は界磁電流を流すことで電磁石となります。回転子は、固定子の回転磁界に引っ張られ、回転します。これが三相同期電動機の原理です。
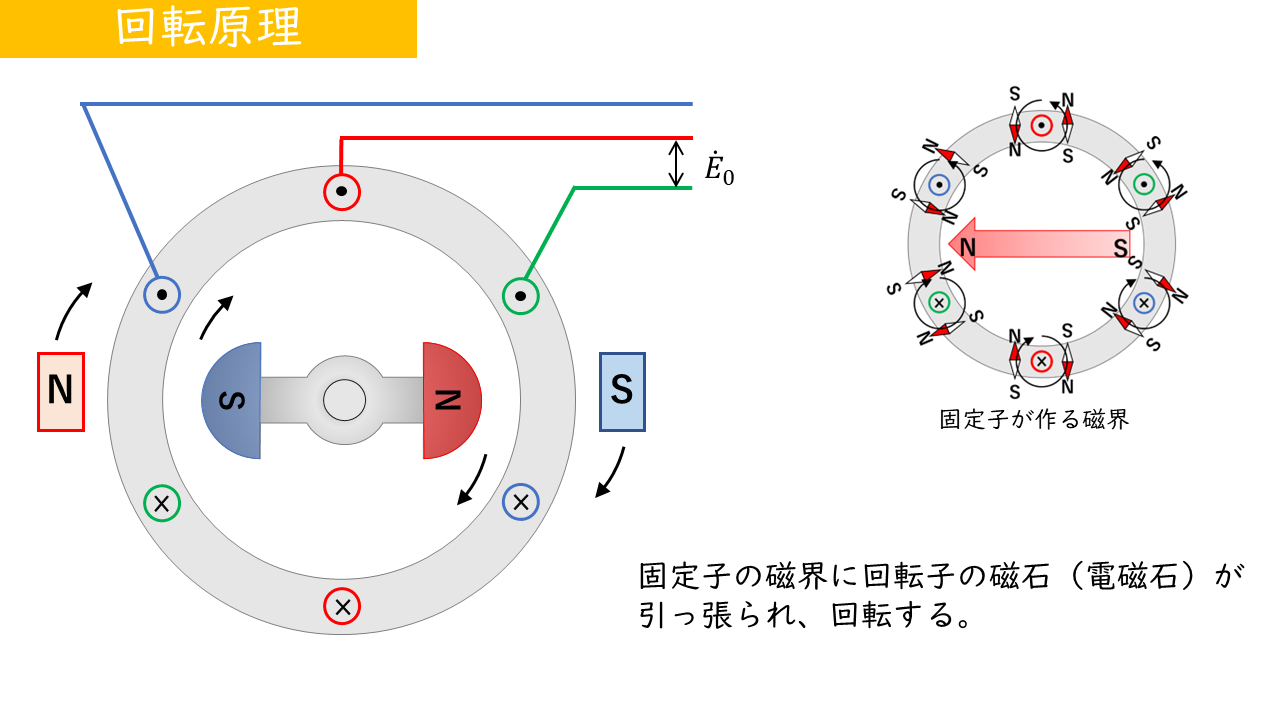
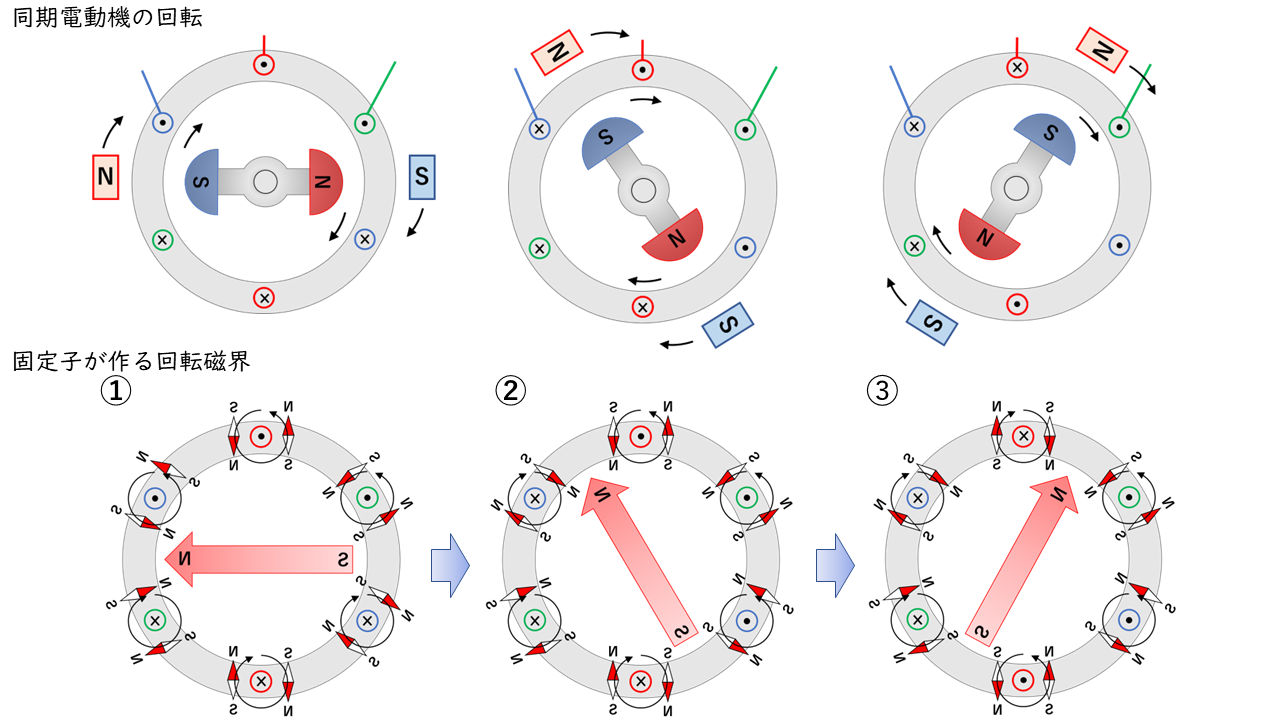
三相同期電動機は、固定子の回転磁界が回転子を磁力によって引っ張るため、2つの回転速度は同じになります(同期しています)。
そのため、同期電動機においては回転速度と同期速度は同じものを指します。
同期速度(回転速度):\( N_s = \displaystyle \frac{120f}{p} \)
\(f\):周波数[Hz]、\(p\):極数
三相同期電動機の始動方法
三相同期電動機は、始動時の回転磁界が早すぎると、回転子が回転磁界についていくことができません。
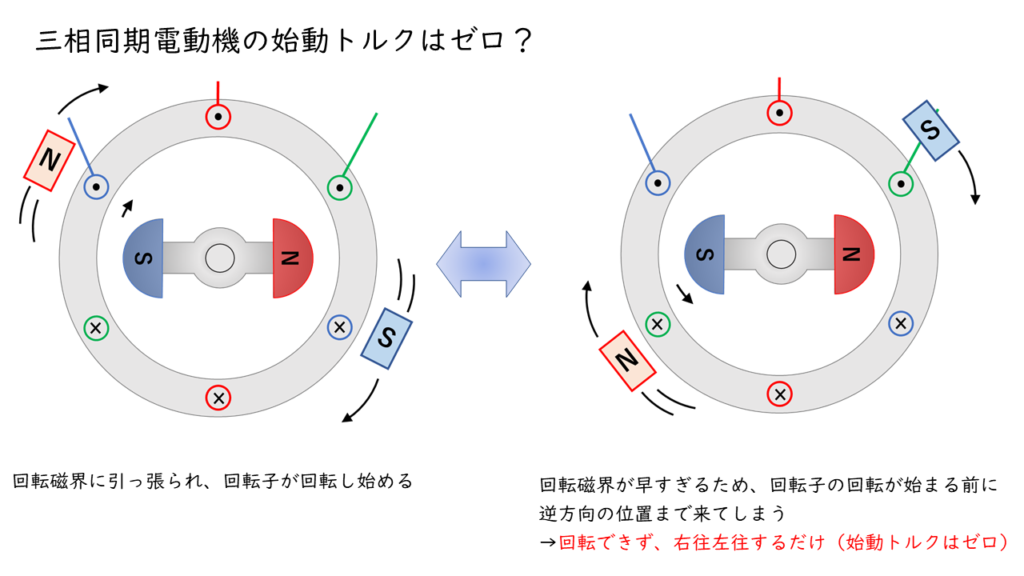
回転磁界に追従できずにいる状態では、回転子が右往左往するだけとなり平均すると始動トルクはゼロとみなすことができます。
このままでは、電動機が回転することはできないため、三相同期電動機の始動には工夫が必要になります。
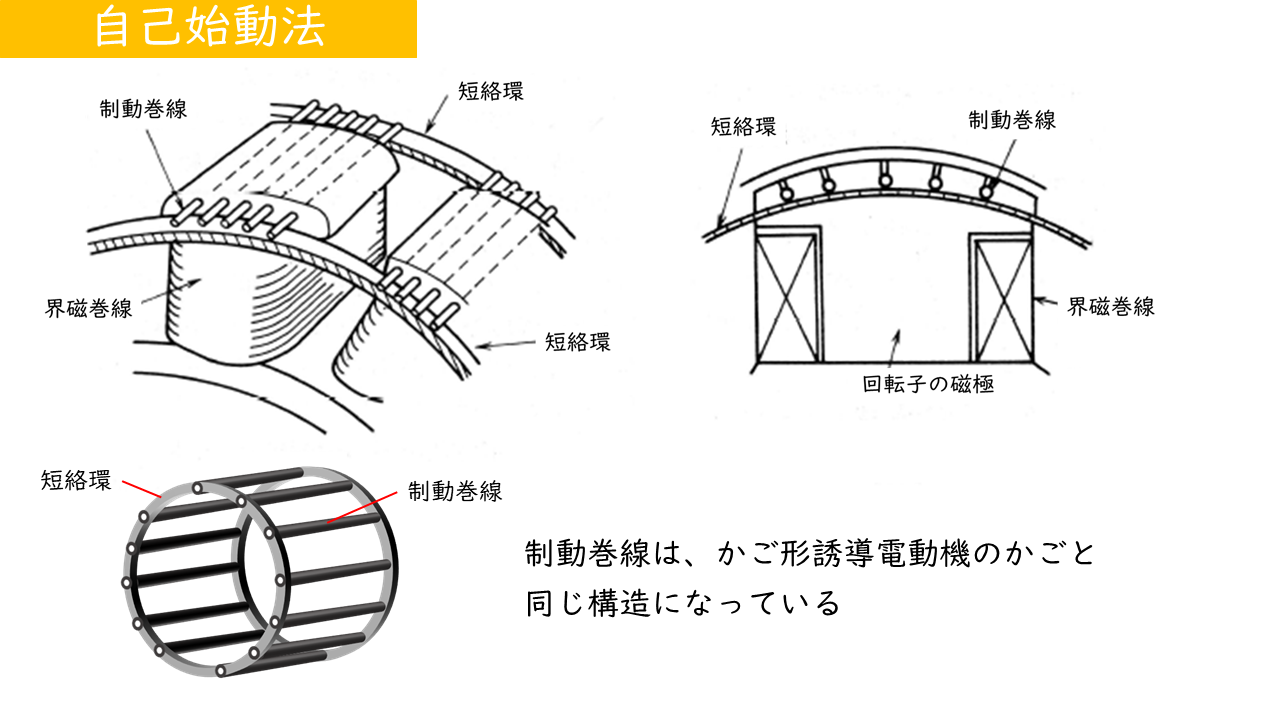
| 自己始動法 | 回転子に制動巻線を設けてかご型誘導電動機として始動トルクを得る |
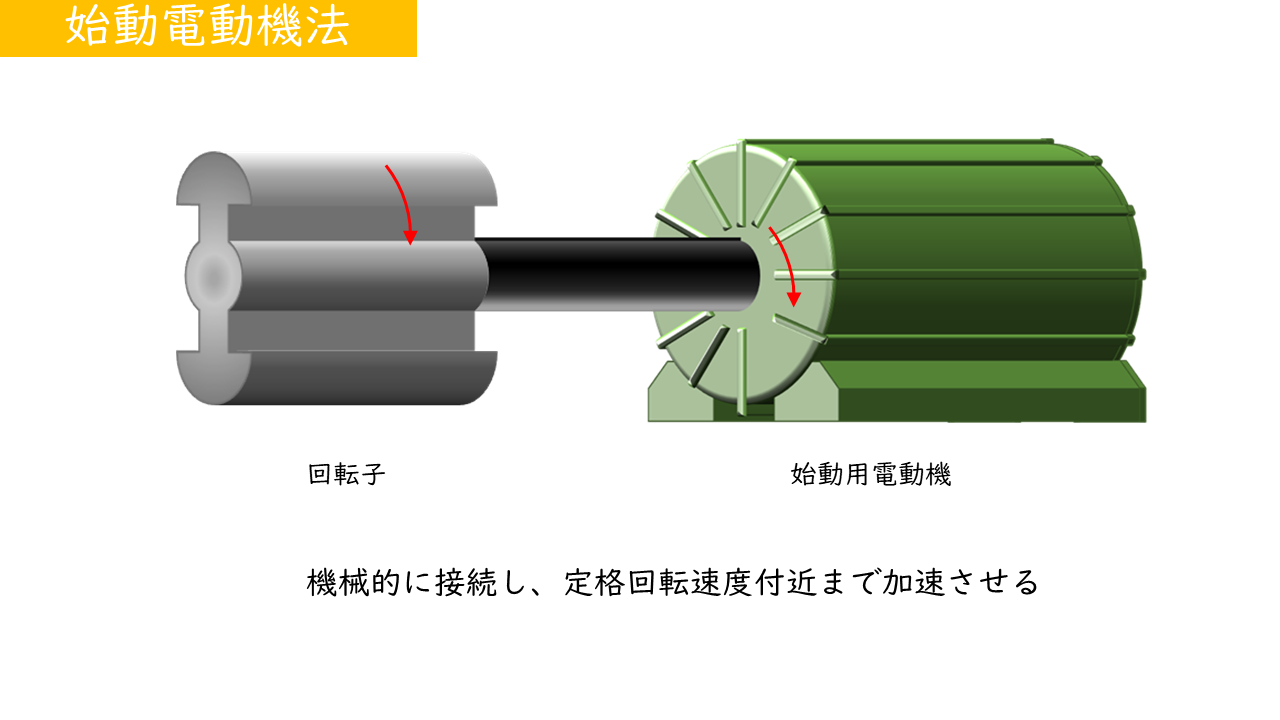
| 始動電動機法 | 同期電動機とは別の電動機により回転子を回転させることで始動トルクを得る |
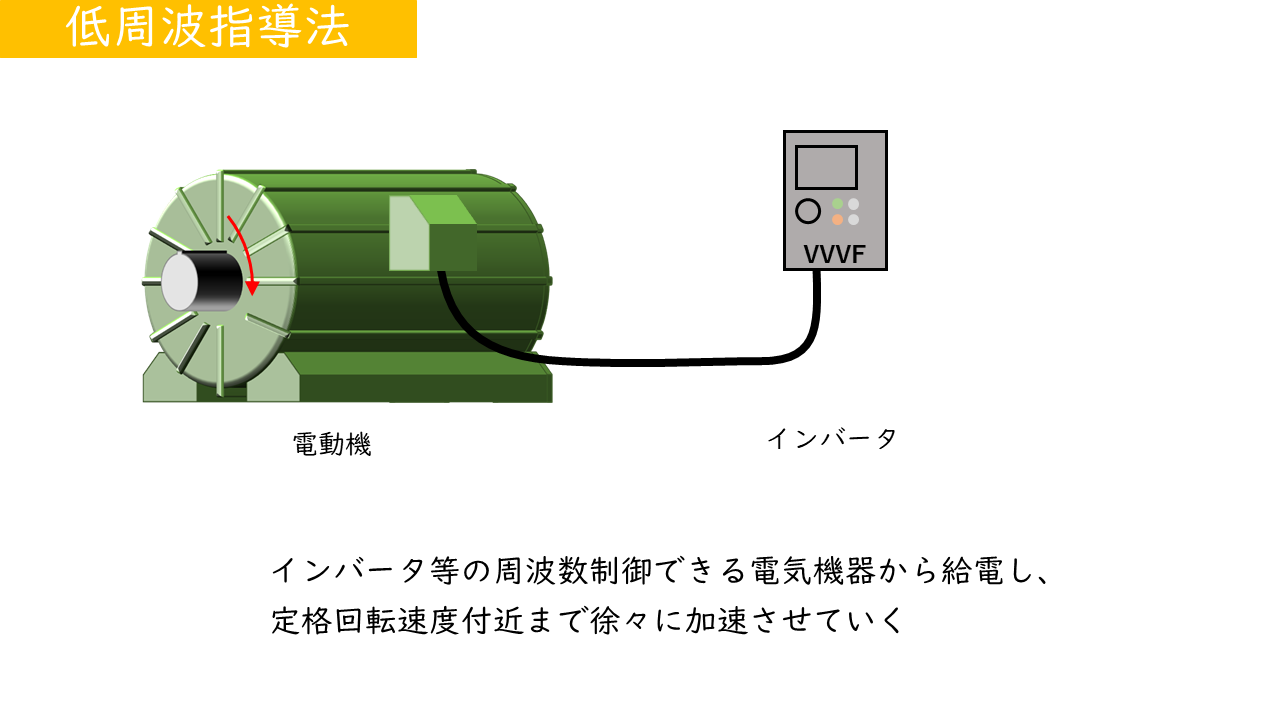
| 低周波始動法 | 回転磁界の回転速度を遅くするため低周波で始動する |
三相同期電動機のトルク
無負荷の場合
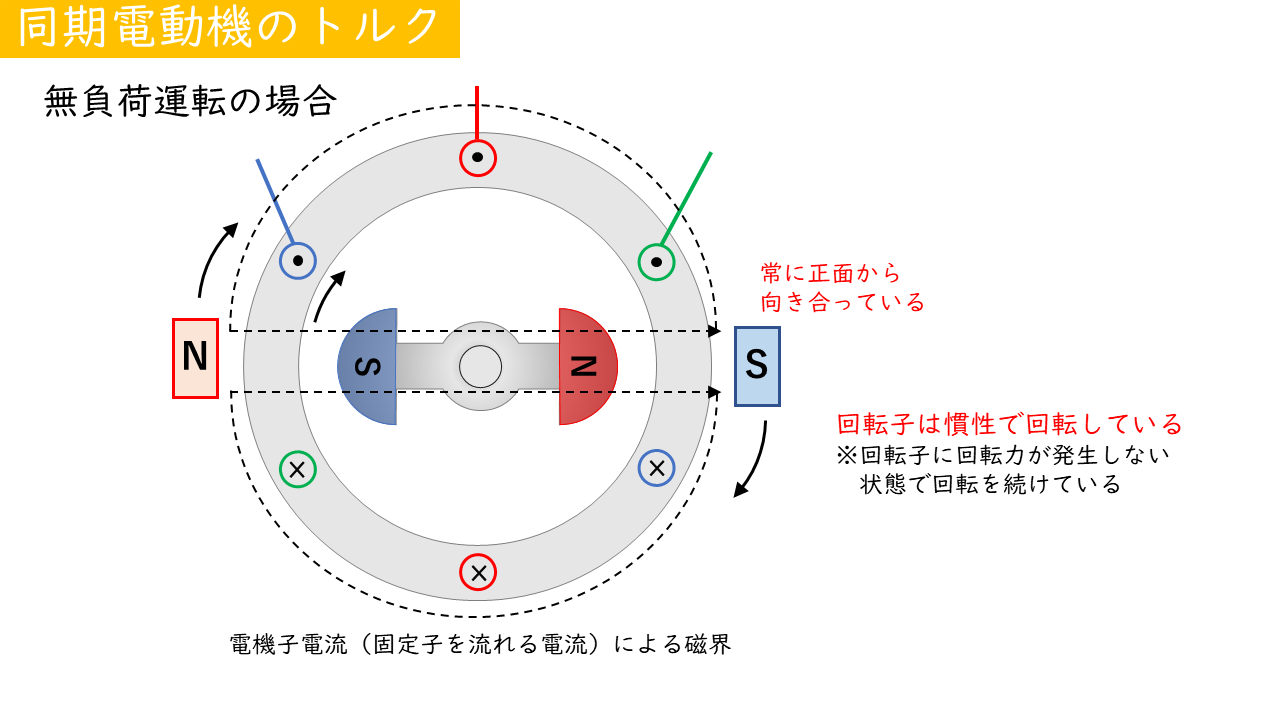
同期電動機が無負荷(ポンプなどとつながっていない状態)で、回転子が回転磁界と同じ角速度で慣性によって回転しているとき、回転磁界によるトルクは発生しません。
回転磁界と回転子の各速度が同じ場合、回転磁界のN極と回転子のS極、回転磁界のS極と回転子のN極が正面い向き合い続ける状態となります。
N極とS極が正面で引き合い続けている状態であるため、回転方向への力が働いていないとみなすことができるため、トルクがゼロと考えます。
負荷をかけた場合
同期電動機に負荷をかけると、回転子の磁極と回転磁界(電機子電流の作る磁界)の磁極が負荷角(トルク角)\( \delta\)[rad]の角度を保った状態で、回転子が同期速度で回転します。
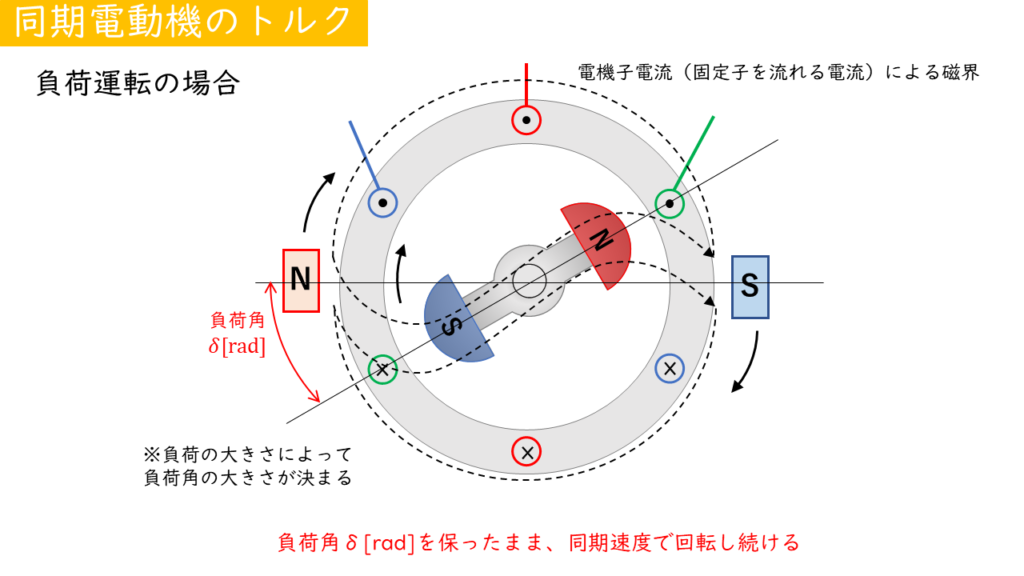
初めに、慣性で回転子が同期速度で回転しているとします。
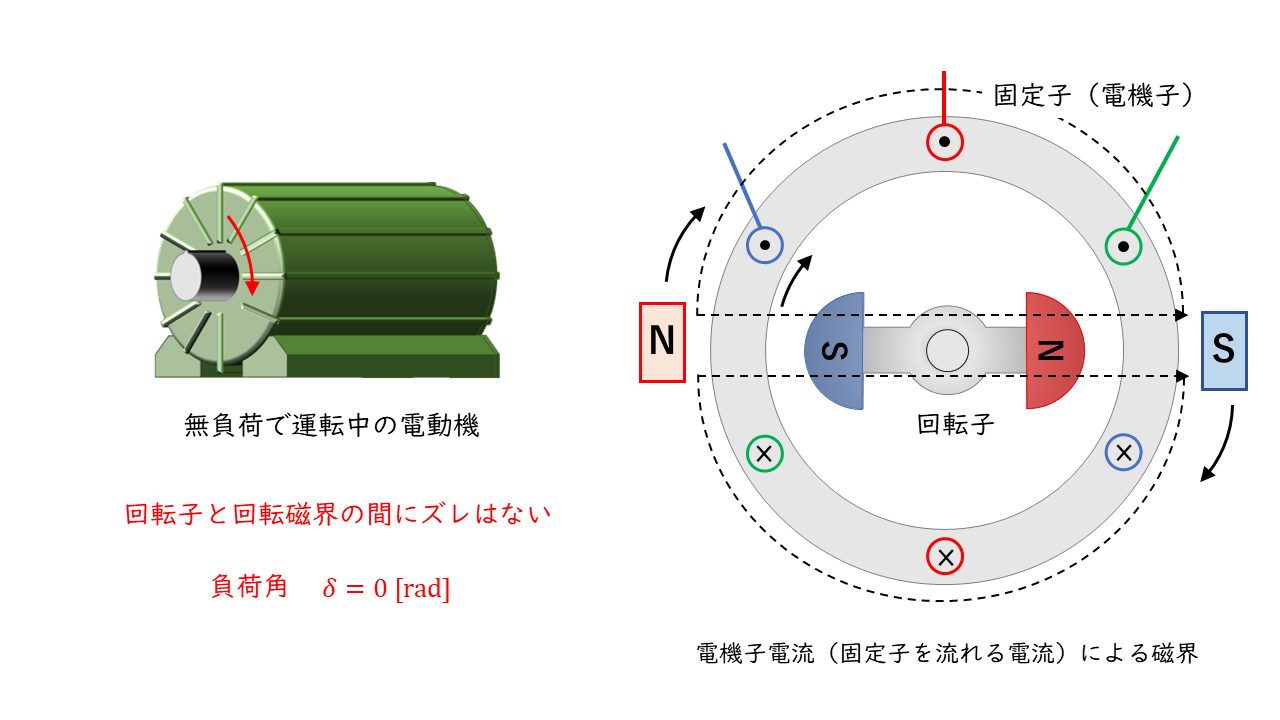
回転子に負荷が接続される(負荷トルクがかかる)と回転子の回転が弱まり、回転磁界と回転子に角度差が生じます。負荷が大きいほど、負荷角\(\delta \) [rad]は大きくなります。
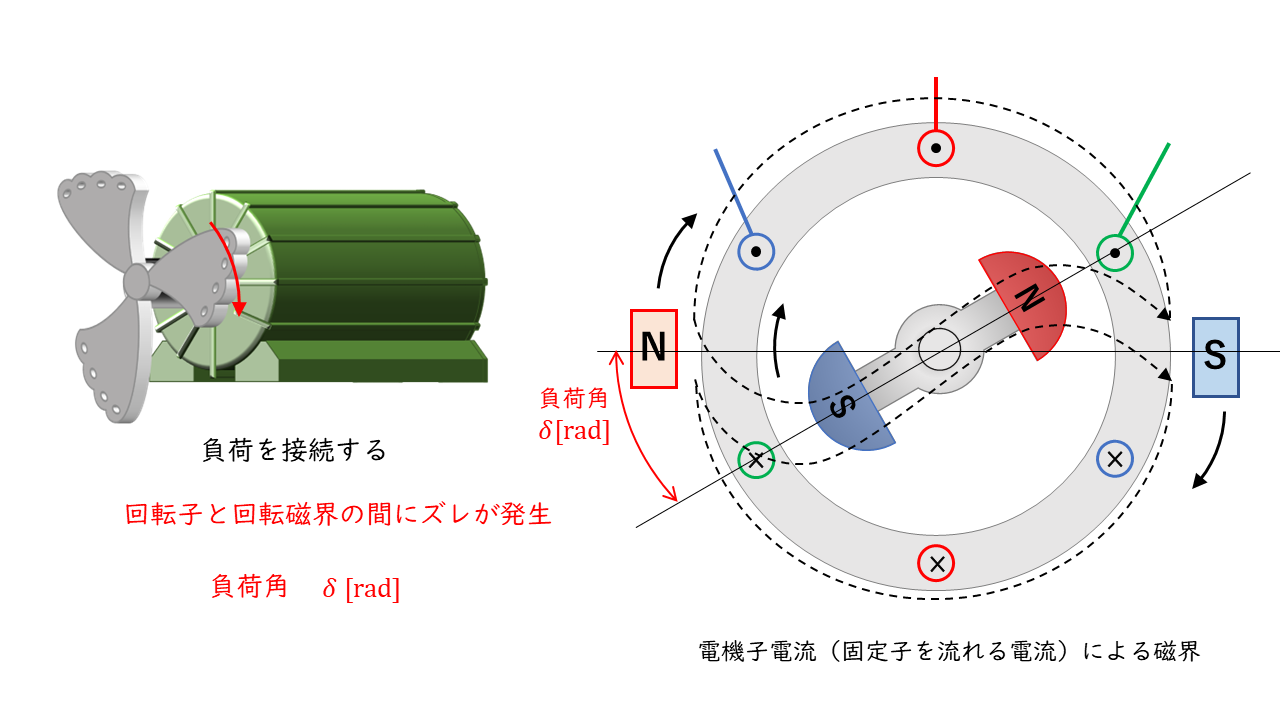
すると、磁石同士が正面から向き合わなくなり、吸引力の一部がトルクに影響を与えるようになります。
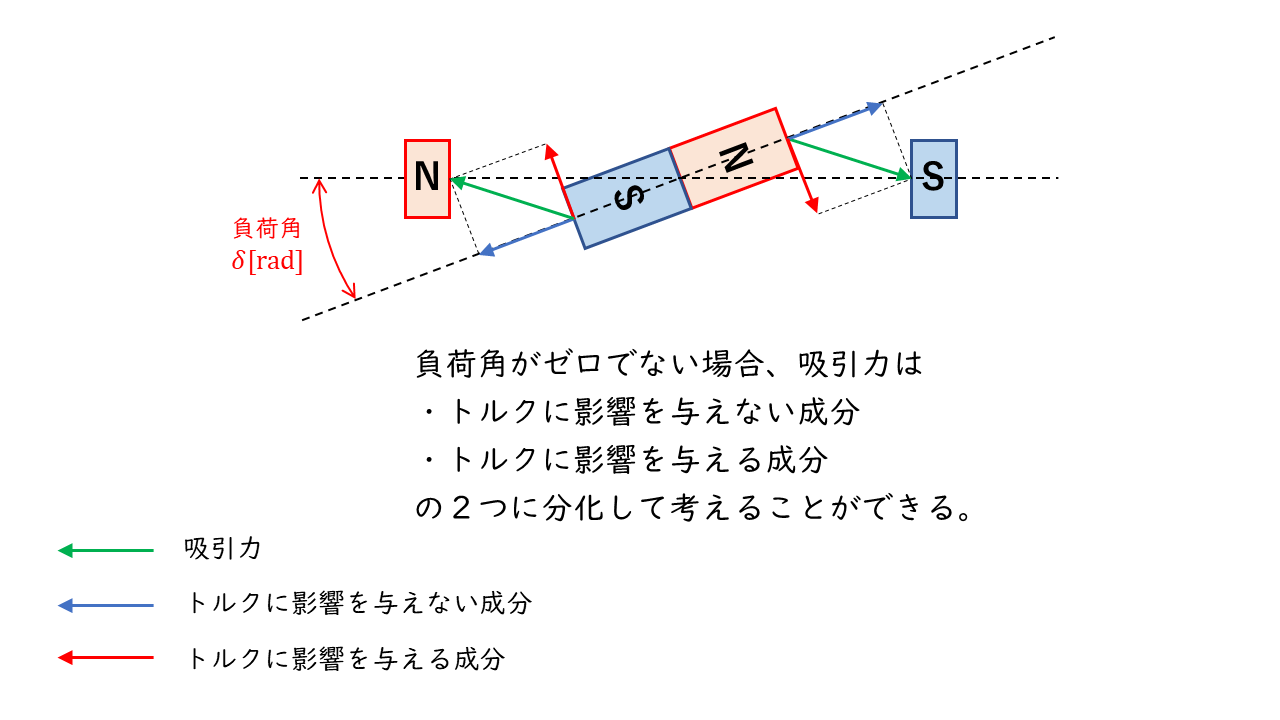
吸引力の一部と負荷トルクがつり合う地点まで来ると、負荷角\(\delta\)[rad]を保ったまま、同期速度で回転し続けます。
トルクって何?という方は、こちらの記事をご確認ください。
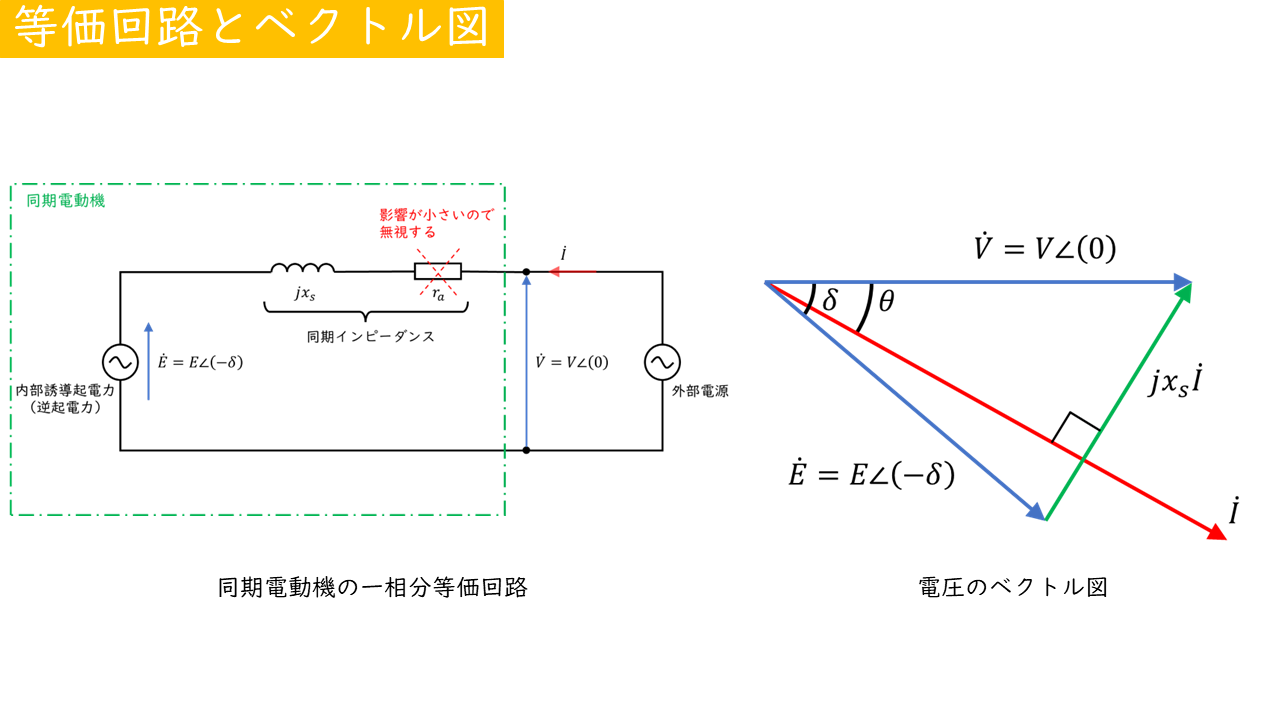
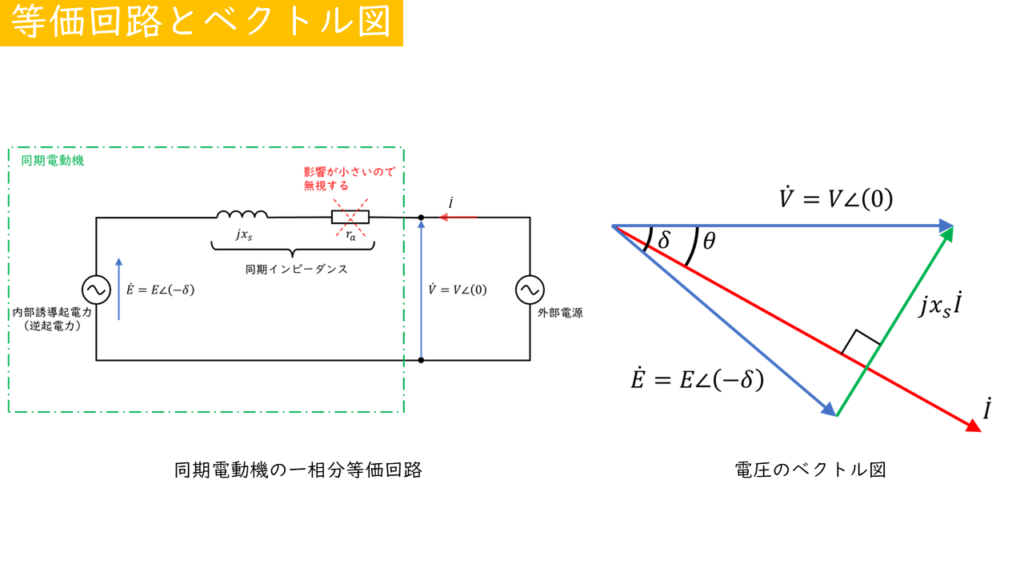
同期電動機の等価回路
同期電動機の一相分の等価回路は、以下のように表すことができます。
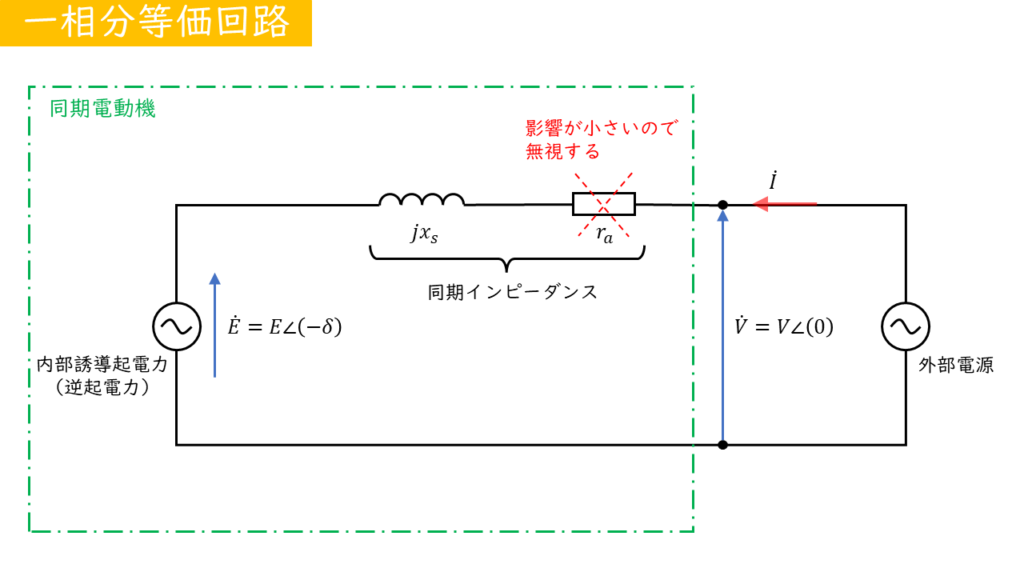
等価回路の形は、同期発電機のときとほとんど変化がありません。ただし、電流の向きが発電機と電動機の場合では逆になっていますので注意が必要です。
等価回路図より、電圧に関する以下の式が成り立ちます。
\( \dot{V} = \dot{E} + jx_s \dot{I} \) [V]
外部電源の電圧\(\dot{V}\)を基準にしたベクトル図を書くと以下のようになります。
一相分の消費電力(有効電力):\(P_1 = E \times I \times \cos \left( \delta – \theta \right) \approx \displaystyle \frac{VE}{x_s}\sin \delta \)
三相分の消費電力(有効電力):\( P_3 = 3P_1 = \displaystyle \frac{3VE}{x_s}\sin \delta \)
一相分の消費電力(有効電力):\(P_1 = E \times I \times \cos \left( \delta – \theta \right) \approx \displaystyle \frac{VE}{x_s}\sin \delta \)
三相分の消費電力(有効電力):\( P_3 = 3P_1 = \displaystyle \frac{3VE}{x_s}\sin \delta \)
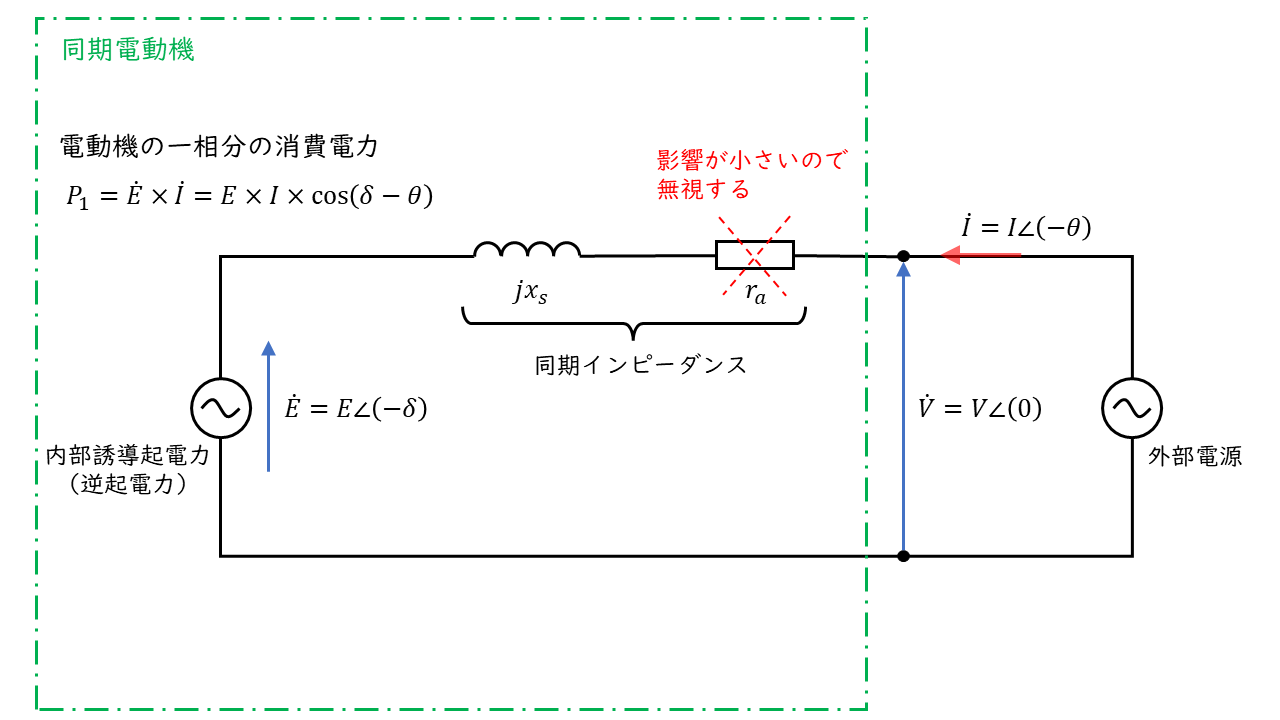
同期電動機の一相分の消費電力(有効電力)\( P_1\) は有効電力を求める計算式より
\(P_1 = E \times I \times \cos \left( \delta – \theta \right) \)
と書き表すことができます。
一相分等価回路のベクトル図より、点AからベクトルOBに垂直な線AHを引く
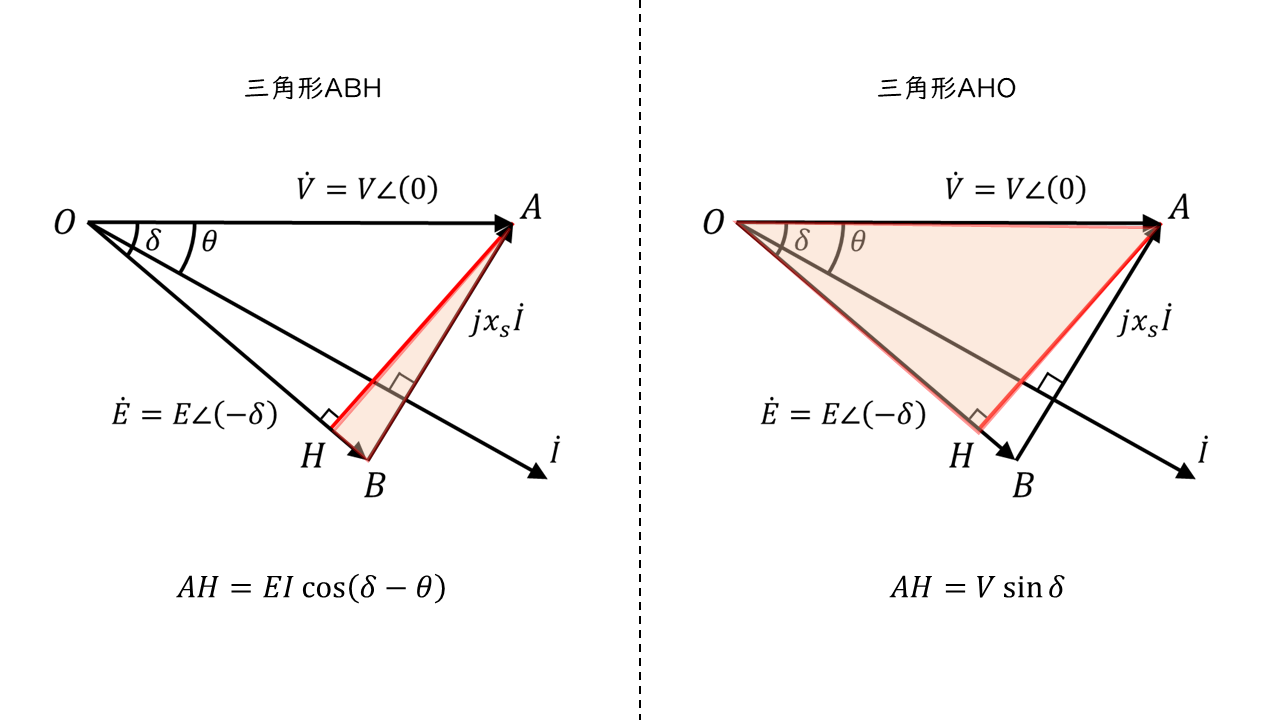
三角形ABHに注目すると、\(AH = x_s I \cos \left( \delta – theta \right) \tag{1} \)
三角形AHOに注目すると、\( AH = V \sin \delta \tag{2} \)
式(1)と(2)より、
\(x_s I \cos \left( \delta – theta \right) = V \sin \delta \)
となるので、消費電力の式は、
\(\begin{align} P_1 &= E \times I \times \cos \left( \delta – theta \right) = E \times \displaystyle \frac{V}{x_s} \sin \delta \\ &= \displaystyle \frac{EV}{x_s}\sin\delta \end{align} \)
以上のようにして、一相分の消費電力(有効電力)を計算することができます。
三相分の消費電力は、一相分の消費電力の3倍したものなので、
\(P_3 = 3 \times P_1 = \displaystyle \frac{3EV}{x_s}\sin\delta \)
と表すことができます。
内部誘導起電力(逆起電力)とは?
同期発電機において、回転子を回転させると固定子(電機子)に誘導起電力が発生することを学習しました。同期電動機の等価回路に現れる内部誘導起電力もこれと同じようなものです。

同期電動機では、回転子が回転磁界よりも負荷角\(\delta\)[rad]分だけ遅れて回転しています。このズレ(負荷角)によって、誘導起電力\(E\)[V]が発生します。
同期電動機の特性
電機子反作用
同期電動機の電気子反作用は、同期発電機の場合の逆となります。これは、電動機として利用する場合と、発電機として利用する場合の電流の流れが逆向きであることに起因しています。
負荷角とトルクの関係
負荷角\(\delta\)とトルク\(T\)の関係をグラフで表すと、以下の図のようになります。
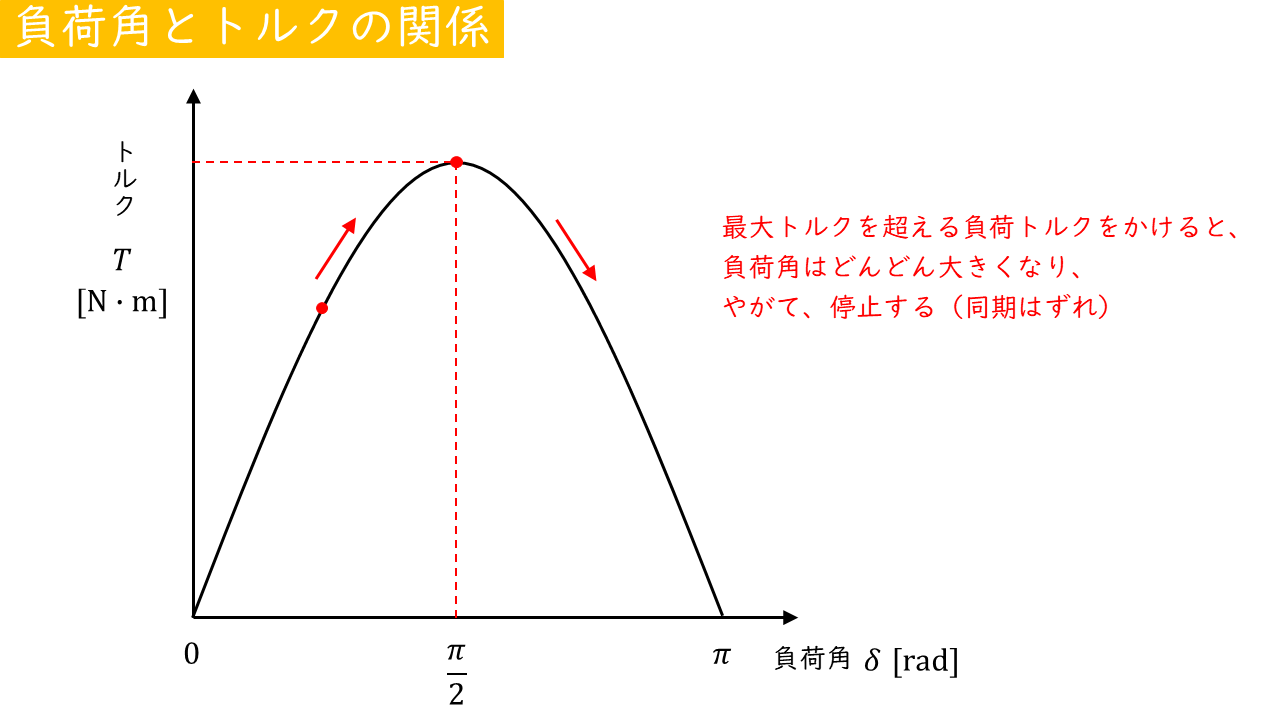
負荷が大きいほど、負荷角\(\delta\)[rad]が大きくなっていきます。負荷角が\(\displaystyle \frac{\pi}{2}\)[rad]になったところで、電動機のトルクは最大となり、それ以降は、電動機トルクは減少していきます。
また、最大トルク以上の負荷トルクをかけると負荷角\(\delta\)[rad]は広がり続け、電動機はやがて停止します。
これを同期はずれ(脱調)といいます。
位相特性曲線(V曲線)
三相同期電動機では、界磁電流\(I_f\)[A]を増減させることで、電気子電流\(\dot{I}\)[A}の大きさと電源電圧\(\dot{V}\)に対する位相の2つを変化させることができます。
界磁電流を増加させると、回転子の磁束が増加し、吸引力が強くなる(増加する)ため、負荷角\(\delta\)[rad]が小さくなります。
反対に、界磁電流を減少させると、回転子の磁束が減少し、吸引力が弱くなる(減少する)ため、負荷角\(\delta\)[rad]は大きくなります。
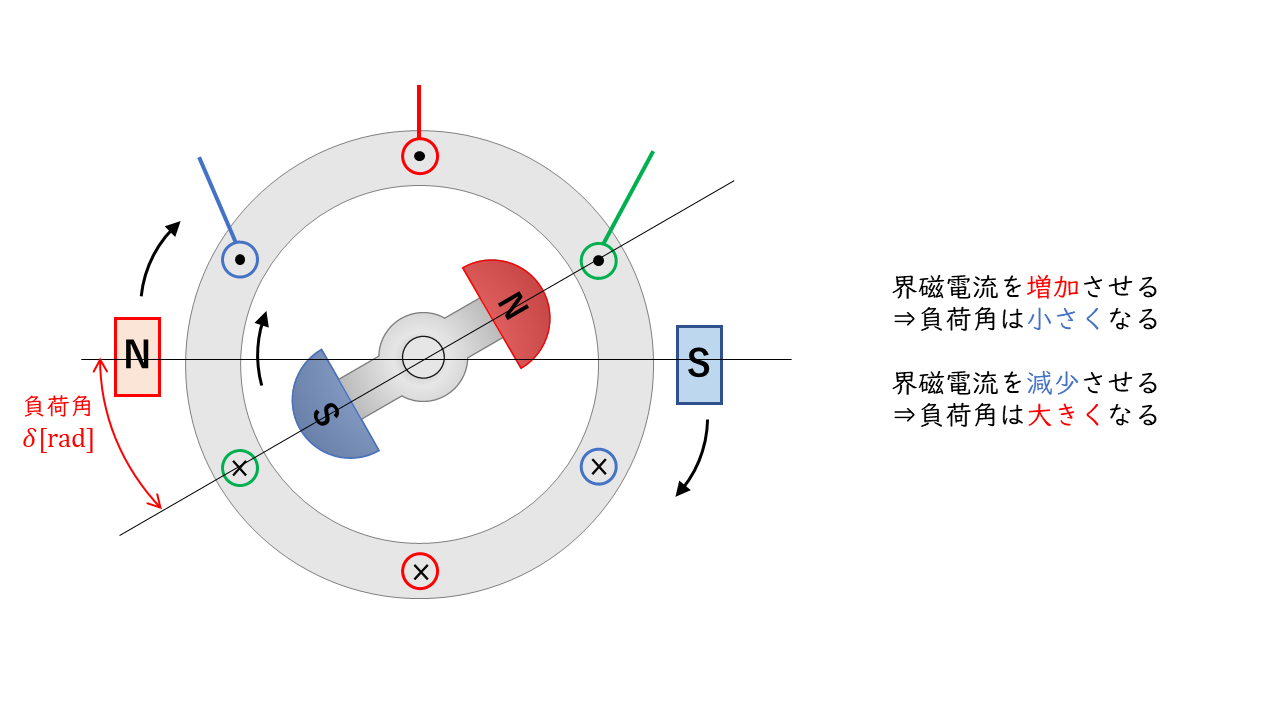
負荷角が変化することで、誘導起電力(逆起電力)\(\dot{E}\)[V]の電源電圧\(\dot{V}\)[V]に対する位相が変化します。これに伴って、電機子電流\(\dot{I}\)[A]の電源電圧\(\dot{V}\)[V]に対する位相も変化します。
位相特性曲線(V曲線)とは、三相同期電動機の界磁電流\(I_f\)[A]と電機子電流の大きさ\(I\)[A]の関係をグラフに表したものです。
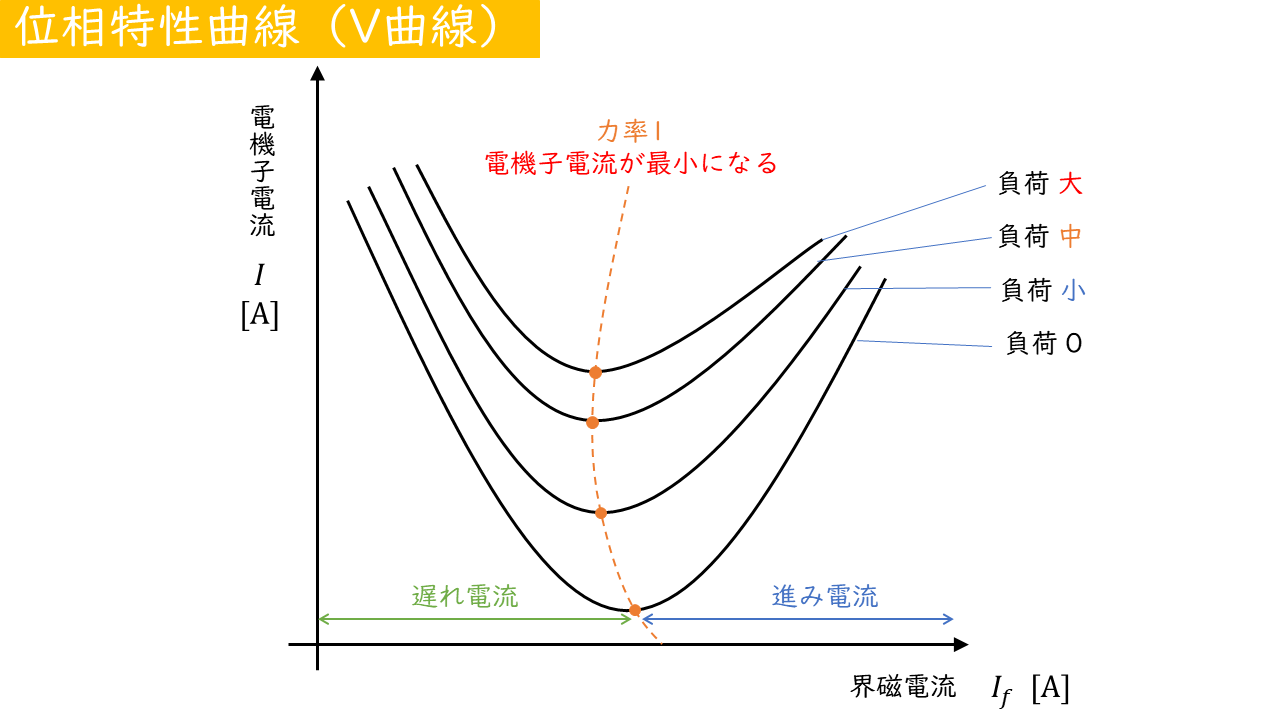
- 力率が1になるとき、電機子電流が最小になる
- 界磁電流を大きくすると、電気子電流の位相を『進み』に変化させることができる
- 界磁電流を小さくすると、電気子電流の位相を『遅れ』に変化させることができる
以上のような特性があることから同期電動機は、同期調相機としても利用されています。
まとめ




一相分の消費電力(有効電力):\(P_1 = E \times I \times \cos \left( \delta – \theta \right) \approx \displaystyle \frac{VE}{x_s}\sin \delta \)
三相分の消費電力(有効電力):\( P_3 = 3P_1 = \displaystyle \frac{3VE}{x_s}\sin \delta \)
過去の出題例
H19年度 問15
H23年度 問5
H24年度 問16
H26年度 問15
H28年度 問5
R元年度 問5
R2年度 問5
R3年度 問5
R4年度下期 問4








コメント