電験三種 電磁気分野では,電流の作る磁界に関する問題は頻出の内容です。電流の作る磁界の考え方を理解することで,電磁気分野の解答できる問題の数がかなり増えます。
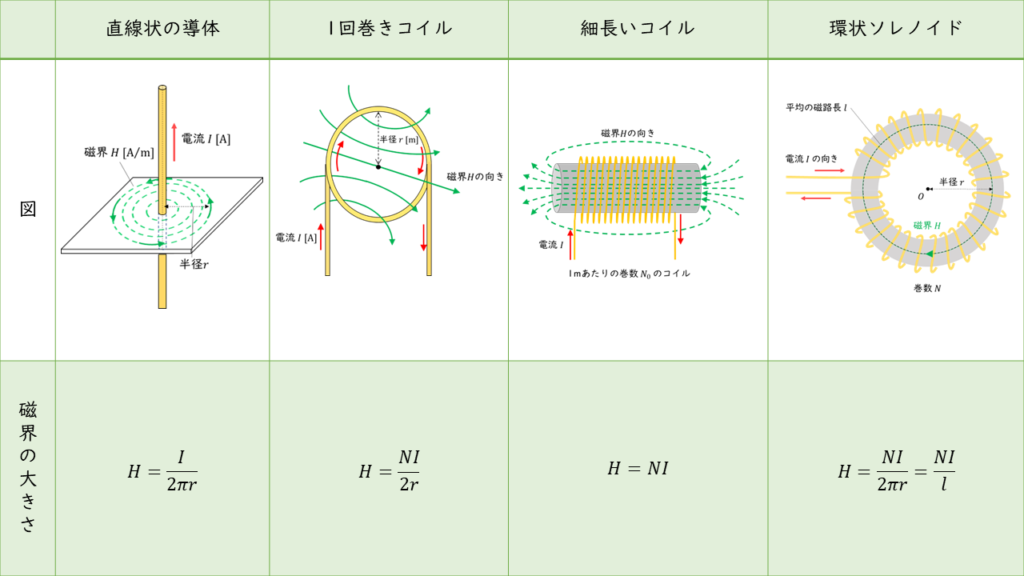
直線導体を流れる電流が作る磁界
下図のように,直線導体を電流が流れるとその周囲には磁界が発生します。
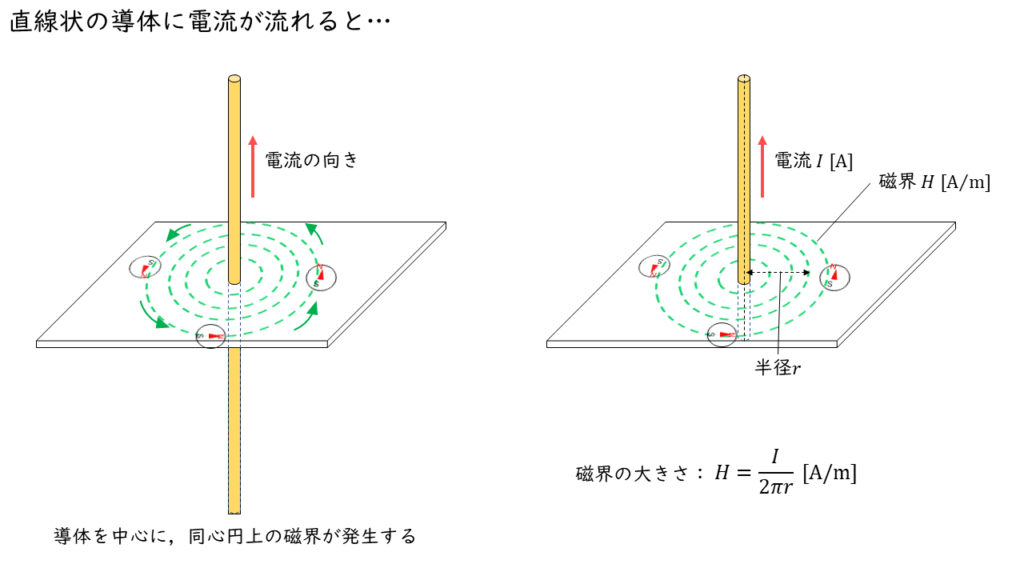
直線導体を中心に同心円状に磁界が発生し,この時の磁界の大きさは以下の式で求めることができます。
\( H = \displaystyle \frac{I}{2 \pi r} \)
\( I \) :電流 [A]
\( r \) :半径 [m]
\( H\) :磁界 [A/m]
また,発生する磁界の向きは「右ねじの法則」によって求めることができます。
右ねじの法則
右ねじの法則とは,「電流の向き」と「磁界の向き」は,「右ねじが進む向き」と「右ねじを回す向き」で決まるという法則です。
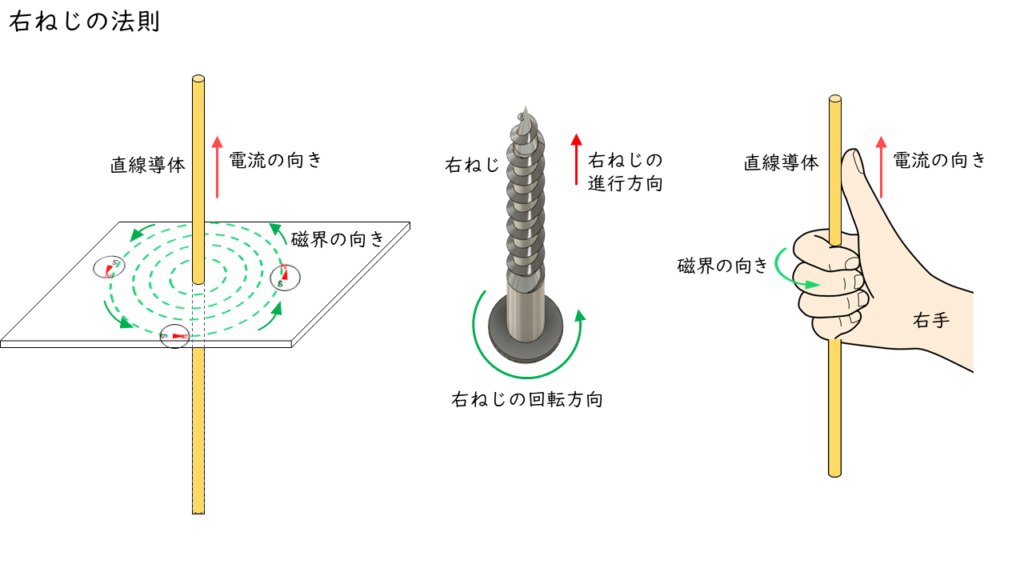
「右ねじ」は,右回り(時計回り)に「ねじ」を回すと,前へ進んでいく「ねじ」のことです。この回転させる方向とねじの進む方向の関係が,直線導体を流れる電流と電流の作る磁界の関係に一致していることから,電流の作る磁界の向きを考える方法として「右ねじの法則」があります。
実際の問題を解くときには,上図のように導体を右手で持つようにし,親指を電流の向きに合わせて考えます。
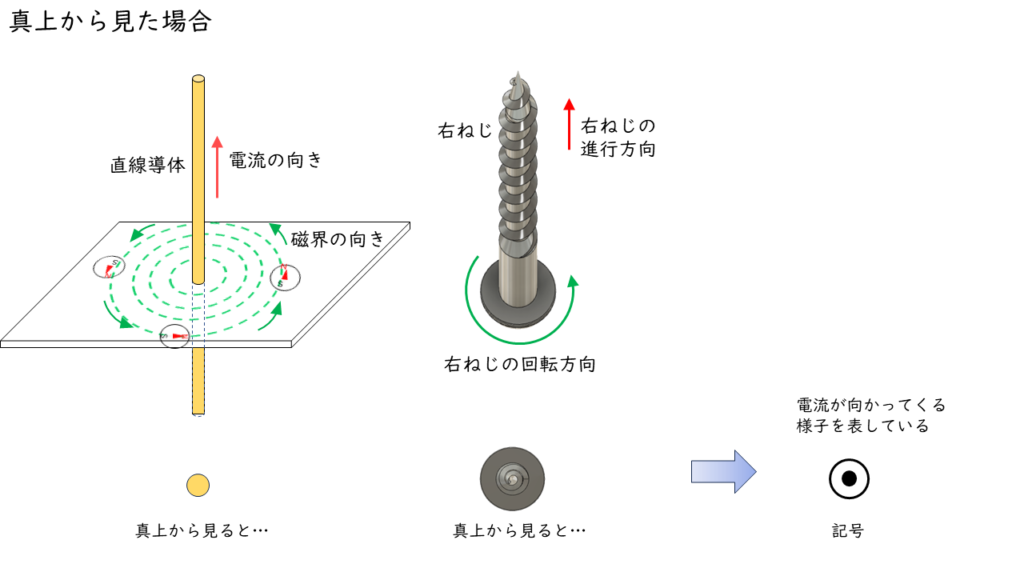
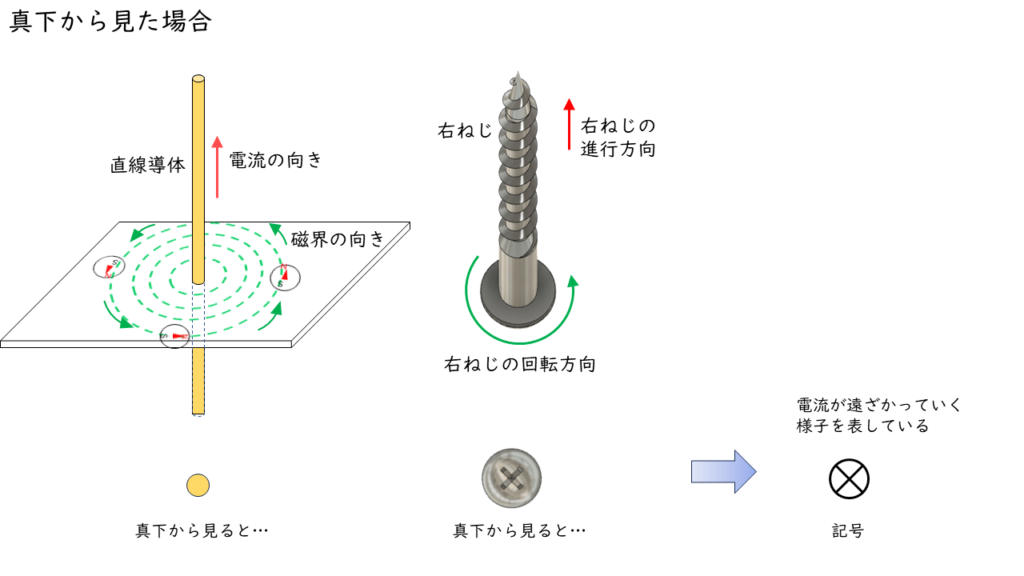
導体を真上(または真下)から見た場合の電流の流れの表し方
電流の作る磁界に関する問では,磁界の様子を図に書き表しやすくするために,導体を真上(または真下)から見た表記をすることがあります。
導体を真上(または真下)から見ると円(点)にしか見えないため,電流の向きを表現するために円の中に以下のような印をつけて電流の向きを表します。
円形導体を流れる電流が作る磁界
導体を曲げて円のようにした場合には,下図のような磁界が発生します。
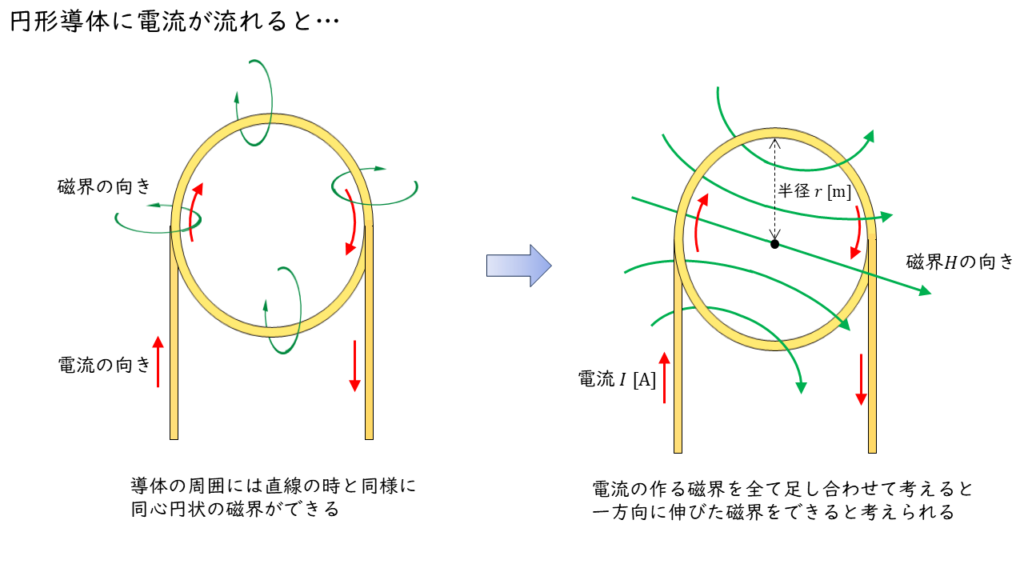
ある一部分の導体に注目すると,直線導体の時と同じように同心円状の磁界を発生させます。しかし,円形導体全体で考えた場合は,一方向に伸びた磁界を発生させると考えることができます。
この時の磁界の大きさは,以下の式で表すことができます。
\( H = \displaystyle \frac{NI}{2 r} \)
\(N\) :導体(コイル)巻数
\(I\) :電流 [A]
\(r\) :半径 [m]
磁界の向きは直線導体の時と同様に右ねじの法則をあてはめることで考えることができます。
問題によっては,電流の向きを優先して書き表す場合があります。その時には,電流と同様の記号を用いて磁界の向きを表します。
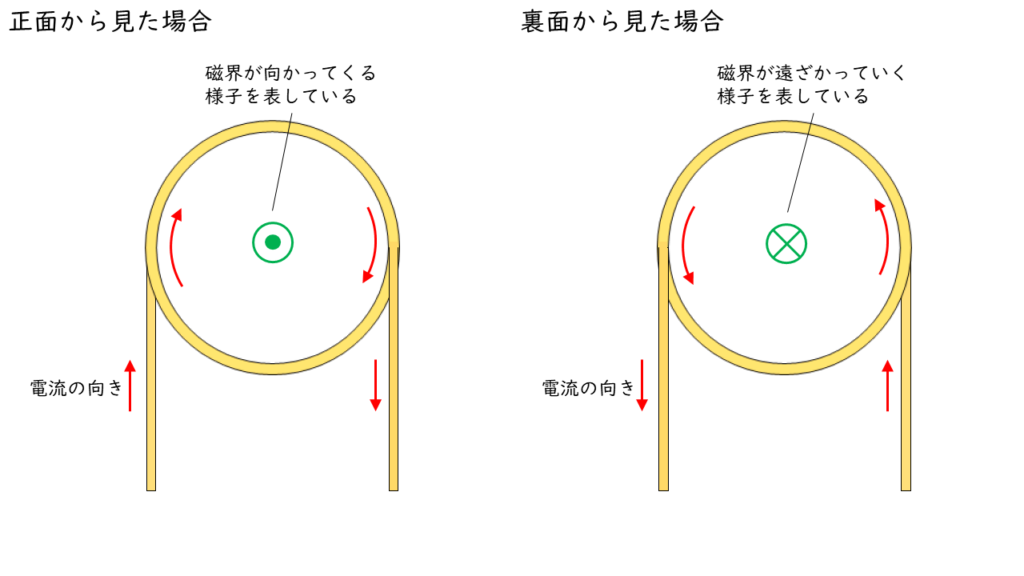
円形導体を流れる電流が作る磁界の式は,「ビオ・バザールの法則」を利用して導出することができます。しかし,ビオ・バザールの法則からの磁界の式の導出は,高い数学の知識が必要になるので,円形導体の式は暗記することをお勧めします。
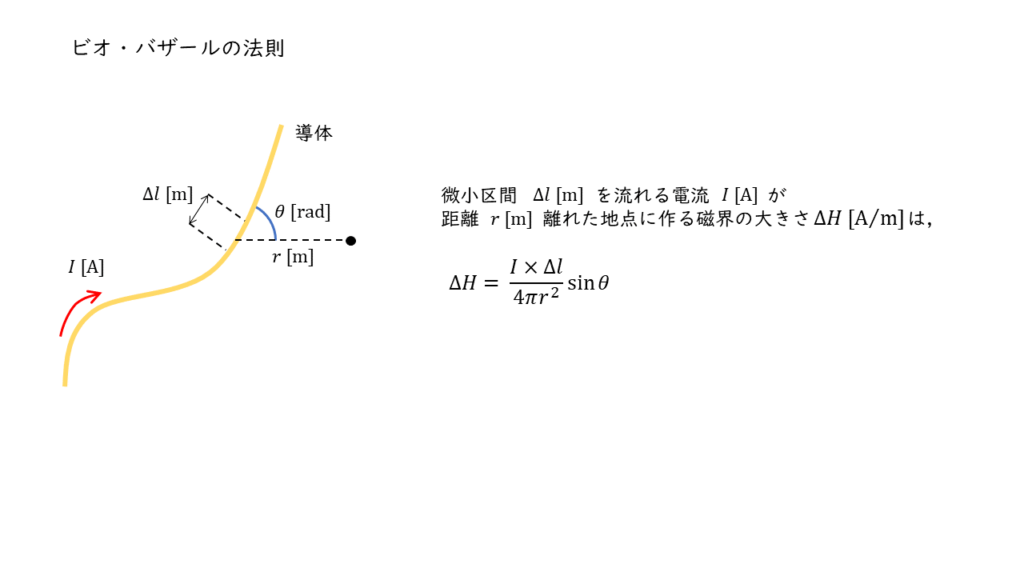
ビオ・バザールの法則とは
「ビオ・バザールの法則」とは,微小区間 \(\Delta l\ \rm m\) に流れる電流が作る磁界 \(\Delta H\ \rm A/m\) を数式で表したものです。
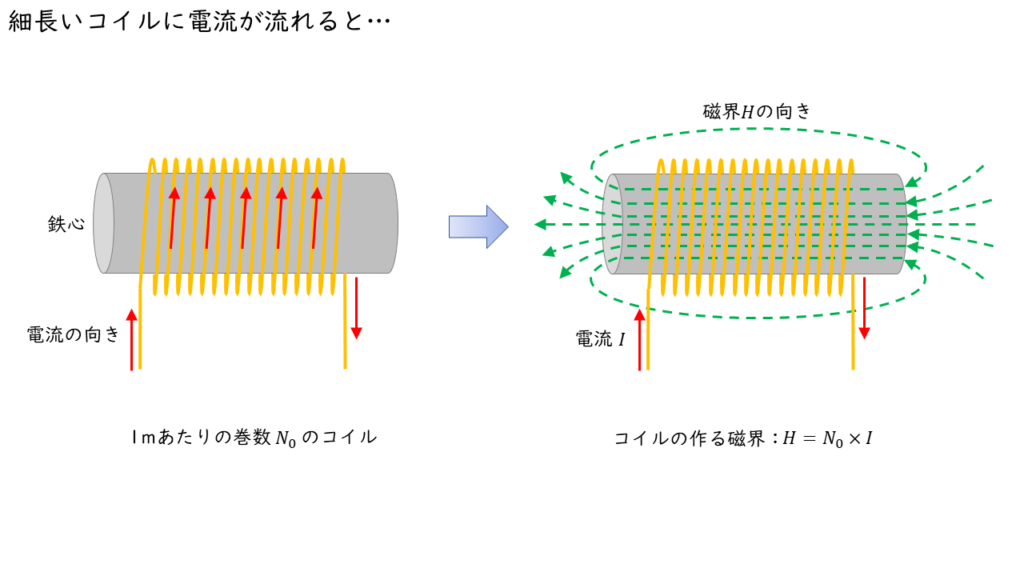
細長いコイルを流れる電流が作る磁界
\( 1 \ \rm m\) あたりの巻数 \(N_0\) 回の細長いコイル(無限長ソレノイド)に電流 \(I\ \rm A\) を流した時にコイルの内部に発生する磁界 \(H \ \rm A/m\) の大きさは,
\( H = N_0 \times I \)
\(N_0\) :1mあたりの巻数
\(I\) :電流 [A]
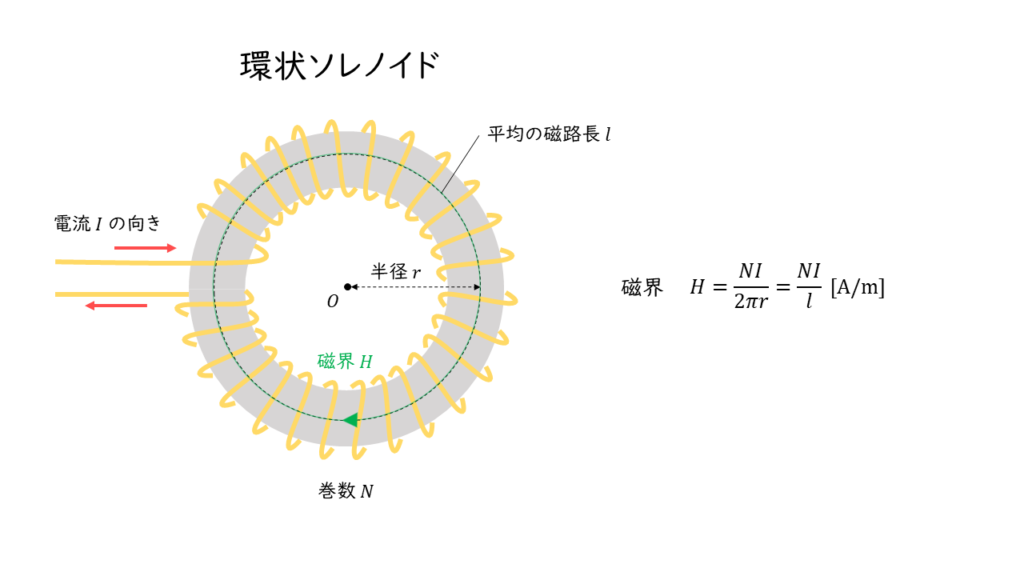
環状ソレノイドを流れる電流が作る磁界
環状ソレノイドとは,輪のような形の鉄心にコイルを一様に隙間なく巻いたものを言います。
\( H = \displaystyle \frac{NI}{2 \pi r} \rm [A/m]\)
\(N\) :巻数
\(I\) :電流 [A]
\(r\) :半径 [m]









コメント