- 自己インダクタンスとは
- 環状ソレノイドの自己インダクタンス
自己インダクタンスとは
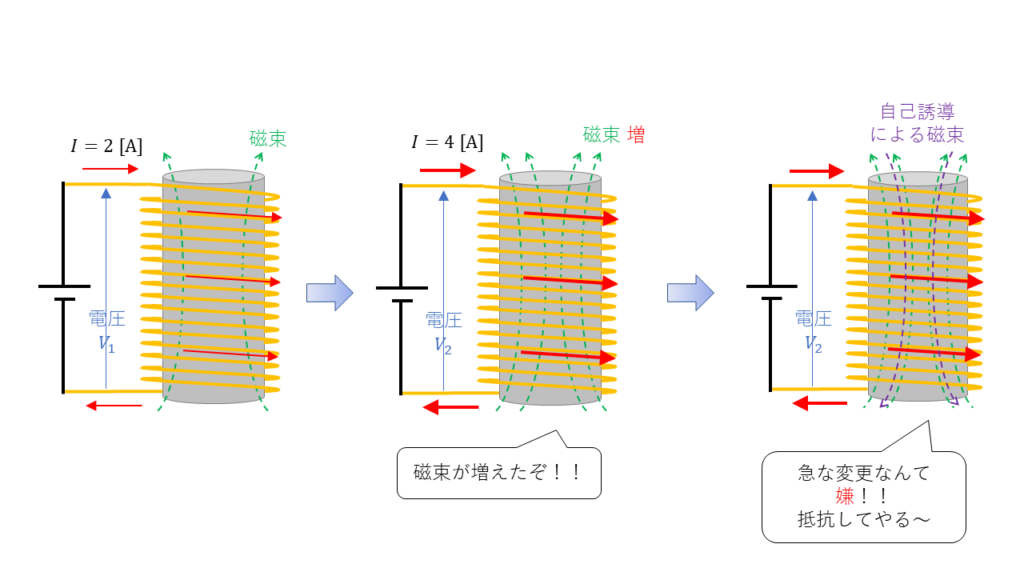
この時、発生した起電力を自己誘導起電力といいます。
誘導起電力は、
$$ e = -N \frac{\delta \phi}{\delta t} [V]$$
で表される。
ここで、電流の変化\( \delta I \) → 電流変化に比例した磁束が変化\( \left( N・\delta \phi \right) \) → 自己誘導起電力eが発生
$$ e = -L \frac{\delta I}{\delta t} = -N \frac{\delta \phi}{\delta t} [V] $$ よって$$ L = \frac{N\phi}{I} $$
誘導起電力:\( e\) [V]
自己インダクタンス:\( L \) [H]
電流変化:\( \delta I \) [A]
時間変化:\( \delta t \) [s]
巻数:\( N\)
磁束変化:\( \delta \phi \) [Wb]
環状ソレノイドの自己インダクタンス
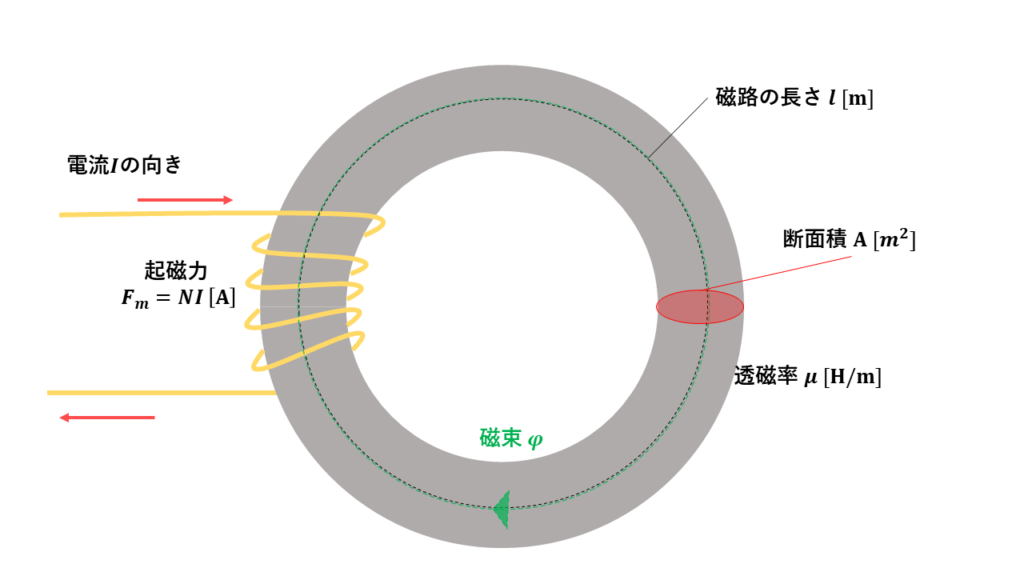
図のように、鉄心の断面積\(A \left[ m^2 \right] \)、磁路の平均長さ\( l \left[ m \right] \)、透磁率\( \mu = \mu_r \times \mu_0 \)としたとき、巻数\( N\)の環状ソレノイドの自己インダクタンス\( L \left[ H \right] \)を求める。
自己インダクタンスの公式より、
$$ L = \frac{N \phi}{I} $$
ここで、鉄心内の磁束密度を\( B \left[ T \right] \)とすると、
$$ \begin{align} \phi &= B \times A \\ &=磁束密度 \times 断面積 \\ &=\mu \times H \times A \end{align}$$
環状ソレノイド内の磁界の大きさは\( \displaystyle H =\frac{NI}{l} \)だから、
$$ \begin{align} \phi &= \mu \times \frac{NI}{l} \times A \\ &=\frac{ \mu_0 \mu_r N I A }{l} \end{align} $$
この式を自己インダクタンスの公式に代入すると
$$ \begin{align} L &= \frac{N \phi}{I} \\ &=\frac{N}{I} \times \frac{mu_0 \mu_r N I A}{l} \\ &=\frac{\mu_0 \mu_r A N^2 }{l} [H] \end{align} $$









コメント