磁界の中を流れる電流には、力(電磁力)が働きます。この原理は、電動機(モーター)の回転原理にも利用されているため、電験を取得するうえで避けては通れない学習範囲です。
計算問題では、\(\sin \theta\)や\(\cos \theta\)などの三角関数を必要とする場面もあり、初学者にはとっつきにくい内容も多くあります。
今回は、計算式の導出書いてもできるだけ図を省かずに解説していきますので、学習の参考にしてみて下さい。
- フレミングの左手の法則
- 電磁力の大きさの計算
- 2本の平行な導体にはたらく力
- ローレンツ力とは
- コイルにはたらくトルクの大きさ
数学が苦手という方は、電験教室のオリジナルテキストでの学びなおしをお勧めしています。
\ 電験教室オリジナル電験三種に特化した数学テキストの購入はこちらから /
電磁力とは?
電流の流れる導体は周囲の磁界から影響を受け、導体に力が働きます。この、導体にはたらく力のことを「電磁力」といいます。
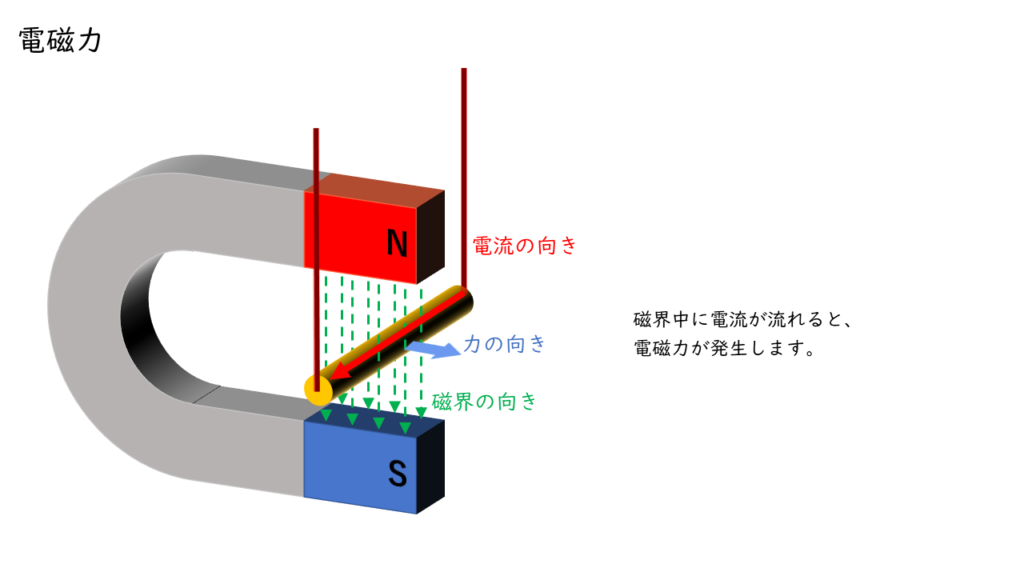
電磁力は”力”なので、”大きさ”と”向き”があります。
フレミングの左手の法則
電磁力の働く向きを求める方法に、「フレミングの左手の法則」があります。
親指、人差し指、中指をそれぞれ下図のように直角になるように広げ、左手の中指を「電流の向き」、人差し指を「磁界の向き」に合わせると、親指が「電磁力の働く向き」を示します。
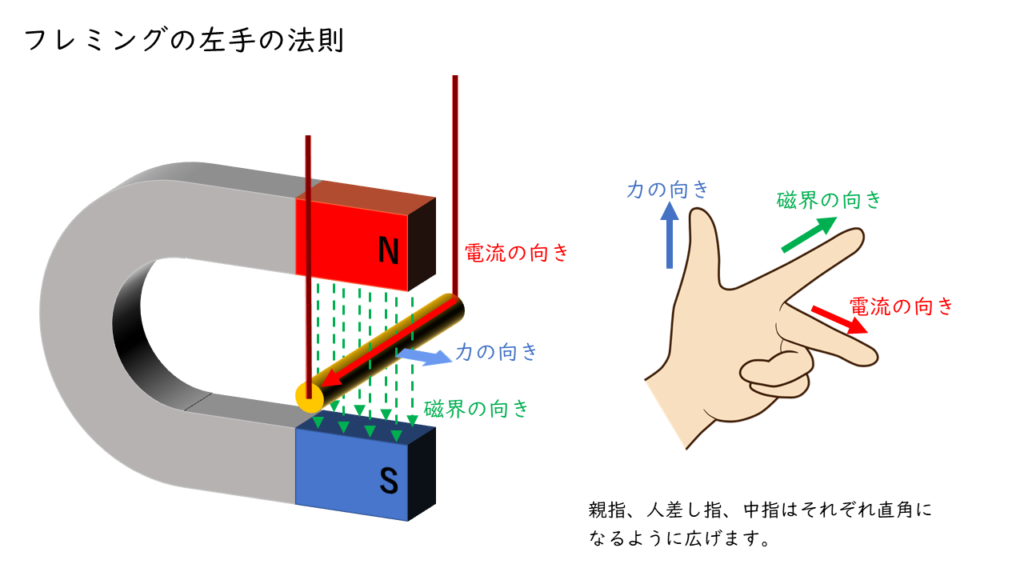
例えば、上図のように、N極とS極の間に導体をぶら下げ、電流を流すと導体が外側へ飛び出すように動きます。実際に、自分の手を使って図のようにあなるかを確かめてみてください。
導体に電流が流れると、その周囲には磁界が発生します。
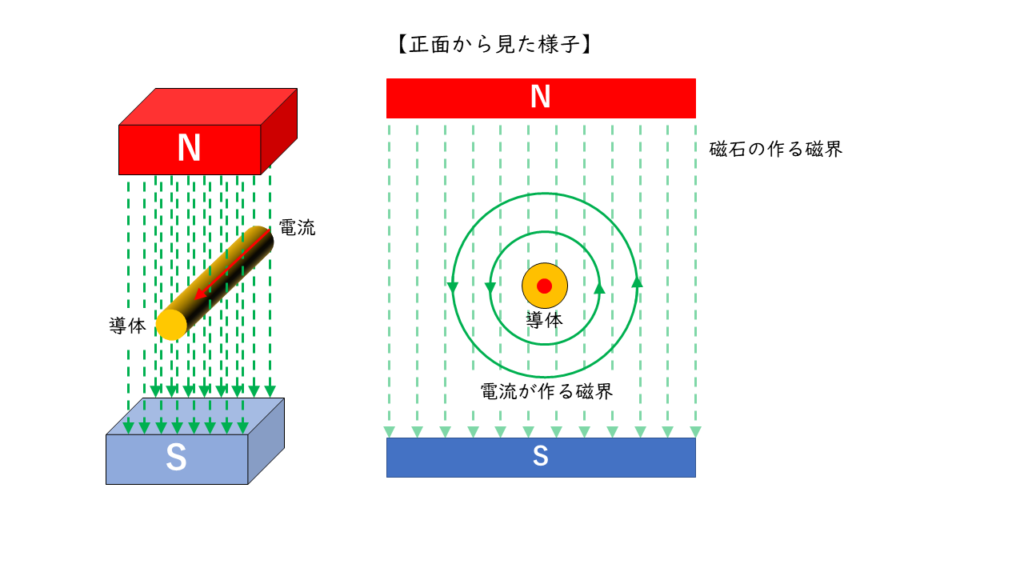
導体を流れる電流による磁界が磁石の作る磁界を乱すことによって導体の左側では磁界が強くなり、右側では磁界が弱くなります。
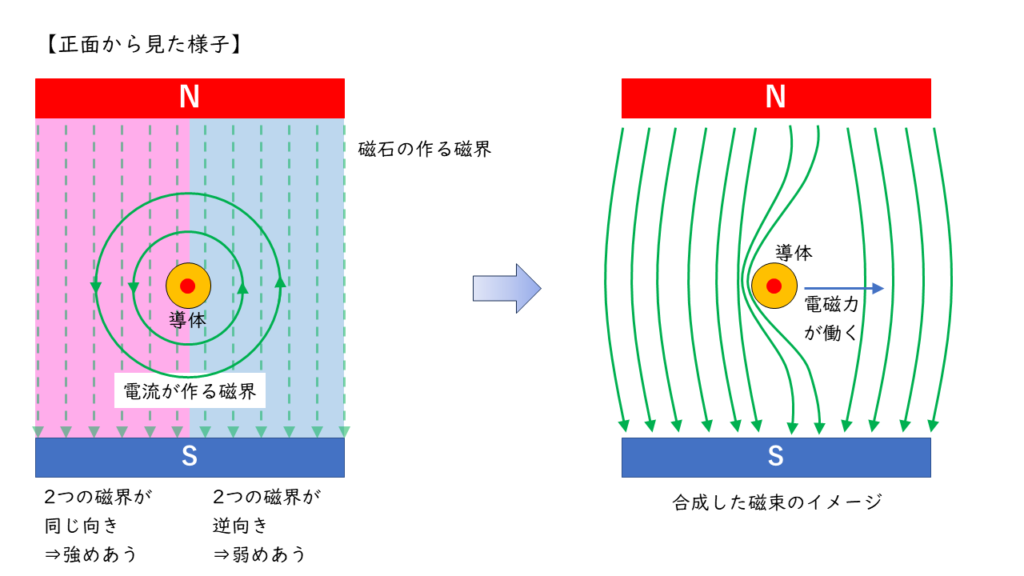
電流の作る磁界によって乱された磁石の磁束は元の状態に戻ろうとする性質があるので、導体は磁束密度の小さい右側へ移動していきます。
電磁力の大きさを求める
電磁力 \(F\ \rm [N]\) の大きさは,磁束密度を \(B\ \rm [T]\) ,磁界と直角に交わる導体の長さを \(l\ \rm [m]\) ,電流の大きさを \(I\ \rm [A]\) とすると,以下の式で計算することができます。
\( F = B \times I \times l \)
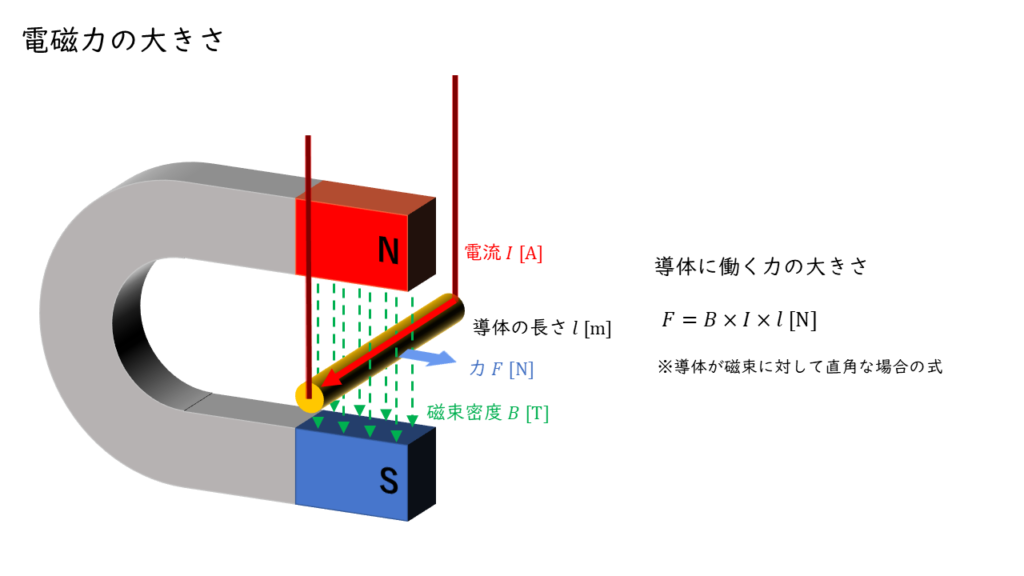
電磁力を考える時に重要なのは、磁界と直角(90度)で交差する成分だけを考える点です。
しかし、電動機(モーター)などの動機械では直角に交わる瞬間ばかりではありません。
次に、直角に交わらない場合はどのように考えていくかを解説していきます。
磁束と導体が斜めに交わる場合の電磁力の計算
磁束に対して導体が直角ではない場合,下図のように補助線を書き加えて,「磁束と直角に交わる成分」と「磁束に平行な成分」に分けて考えます。
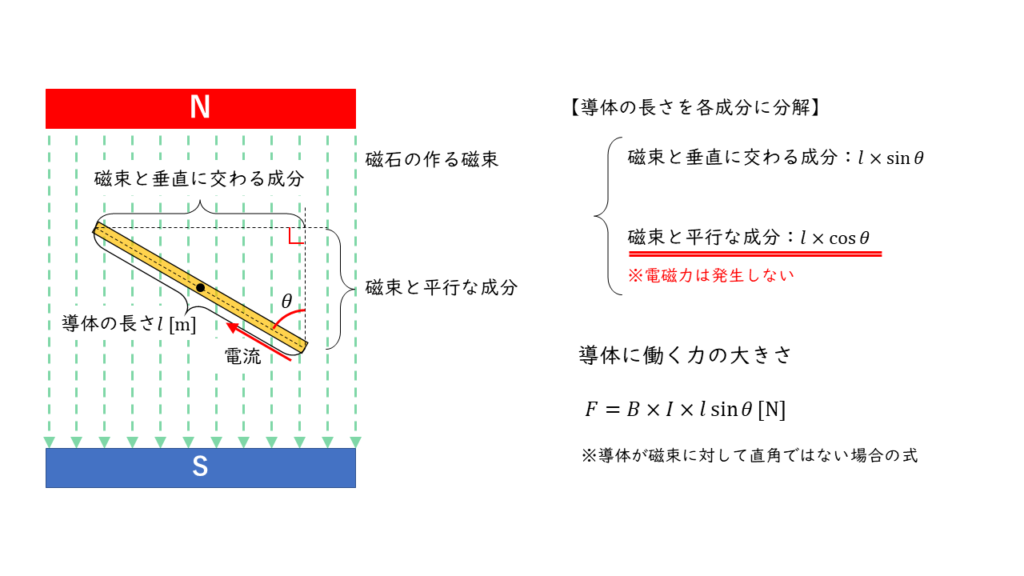
導体が磁界と角度 \(\theta\) で交わるとき,「磁束と垂直に交わる成分」と「磁束と平行な成分」はそれぞれ次のように計算できます。
磁束と垂直に交わる成分: \( l \times \sin\theta \ \rm [m] \)
磁束と平行な成分: \( l \times \cos\theta \ \rm [m] \)
電磁力が発生するのは,磁界と垂直に交わる部分だけなので,電磁力 \(F\) の大きさは次の式で求めることができます。
\( F = B \times I \times l\sin\theta \)
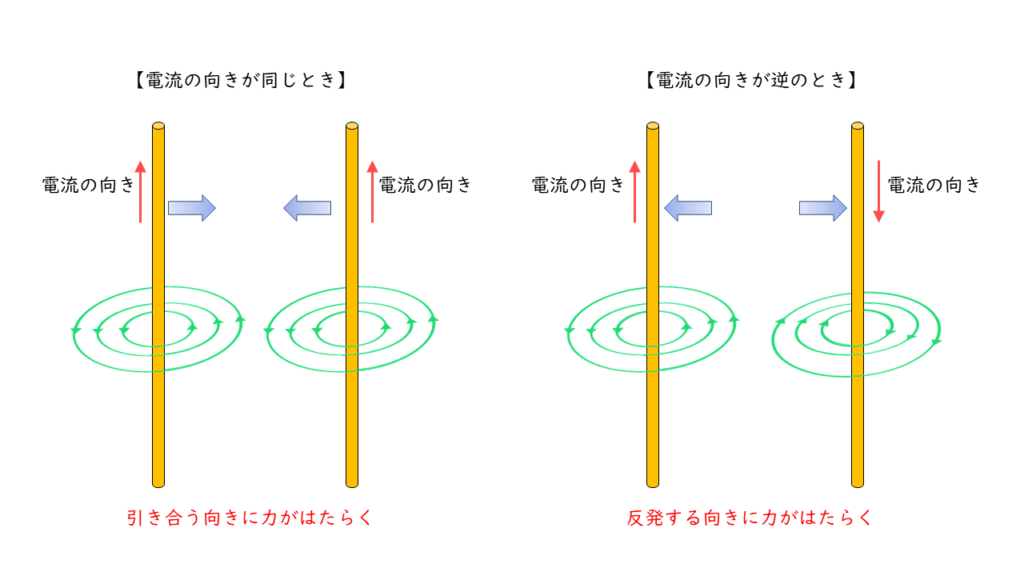
2本の平行な導体間にはたらく力(アンペールの力)
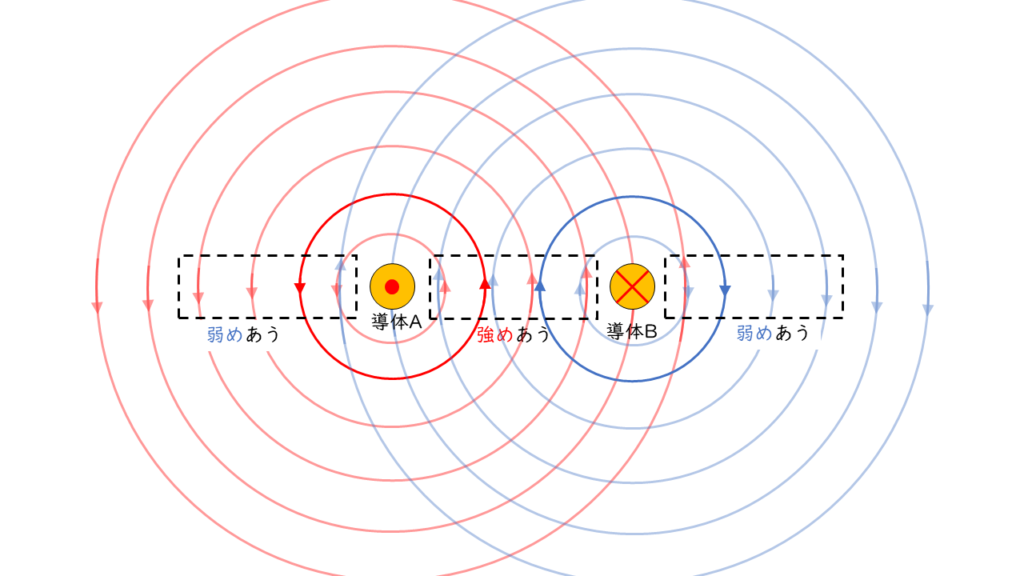
平行に置かれた2本の長い導体に電流が流れる場合,同じ向きに電流を流すと導体同士は引き合い,逆向きに流すと導体同士は反発します。
2本の導体に同じ向きの電流が流れる場合、内側では磁界を打ち消しあい、外側では磁界を強めあうような磁界が発生します。これにより力のつり合いをとるために、導体には内側方向(引き合う方向)に力がはたらきます。
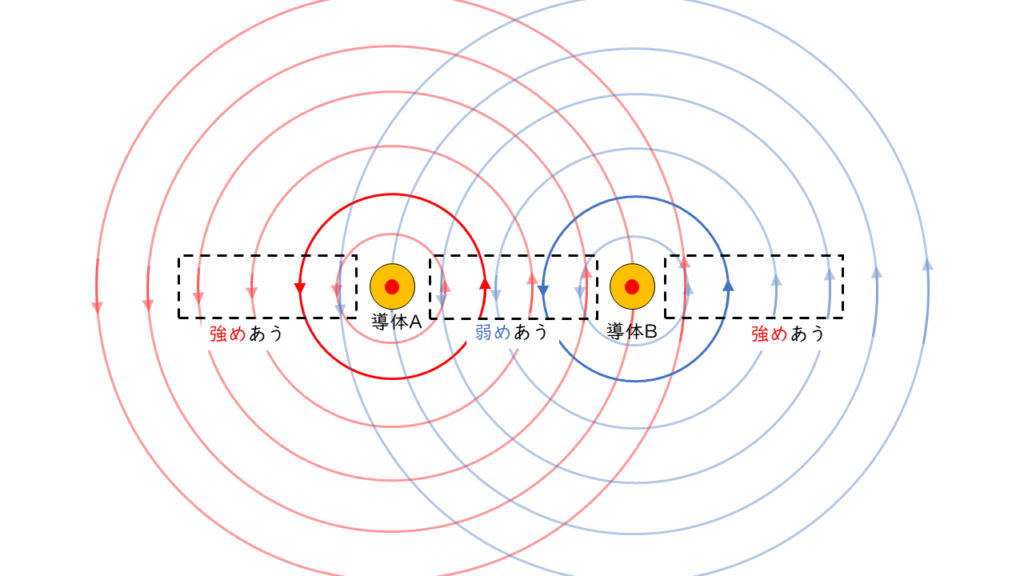
2本の導体に流れる電流が逆向きの場合は、先ほどとは、逆に内側で磁界を強めあい、外側で磁界を弱めあうため反発するように導体に力がはたらきます。
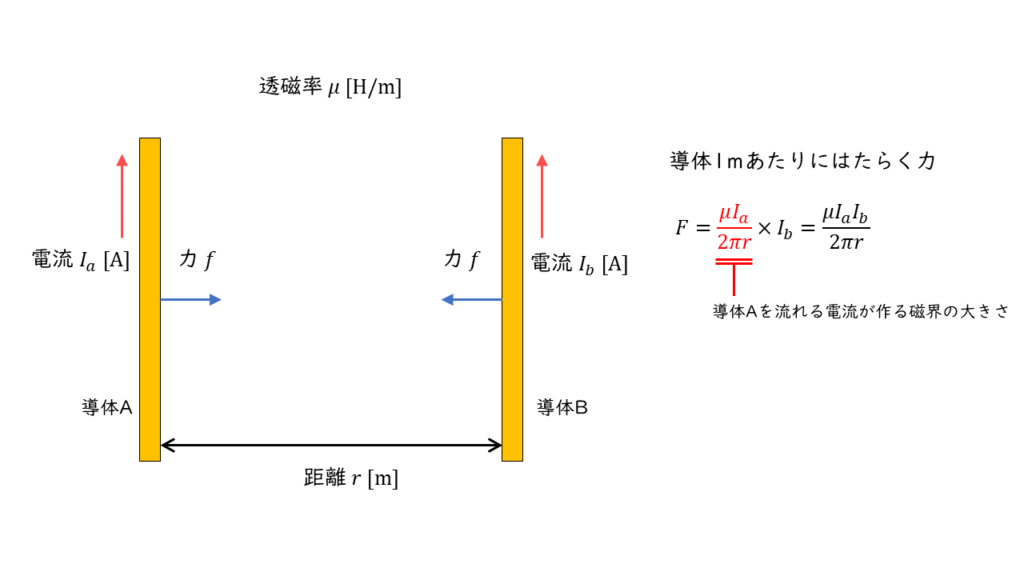
\( F =\displaystyle \frac{\mu I_a I_b}{2 \pi r} = \displaystyle \frac{μ_0 μ_r I_a I_b}{2 \pi r} \)
導体に流れる電流:\(I_a , I_b\ \rm [A]\)
透磁率:\(\mu \ \rm[H/m]\)
導体間の距離:\(r\ \rm[m]\)
真空の透磁率:\(\mu_0\ \rm[H/m]\)
比透磁率:\(\mu_r\)
ローレンツ力
ローレンツ力とは,荷電粒子(電気を帯びた粒)が磁界中を移動する際に磁界から受ける力のことです。
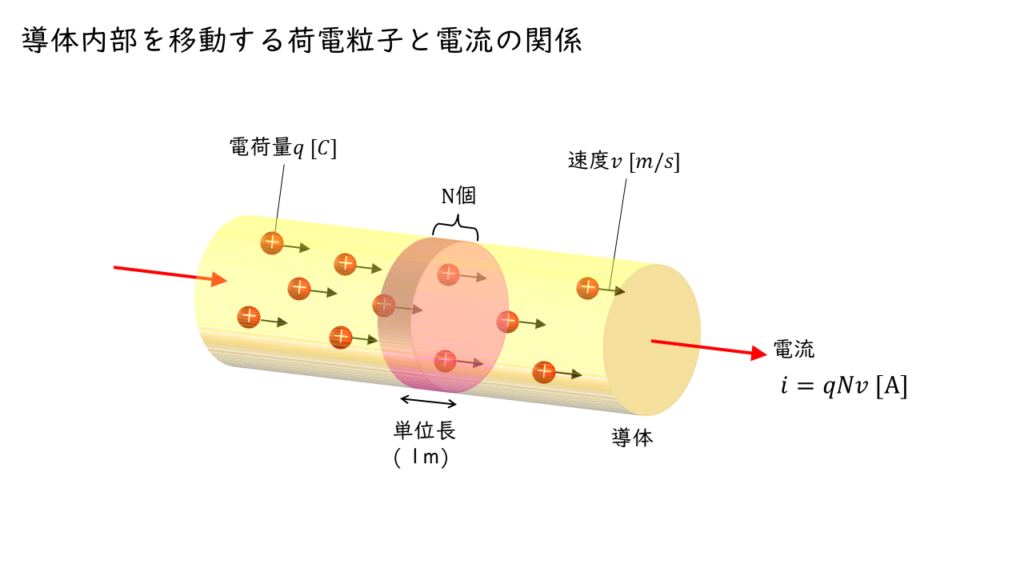
導体の中を移動する荷電粒子1つが持つ電荷を \(q\ \rm[C]\) ,単位長さ \(\left(1\ \rm [m]\right)\) あたりに存在する荷電粒子の数が \(\rm N\ [個/m]\) 移動速度が \(v\ \rm[m/s]\) のとき,電流 \(i\ \rm [A]\) の大きさは
\( i = q \times N \times v \ \rm [A] \)
と表すことができます。したがって、導体に働く力の大きさは,
\(\begin{align} F &= BIl \\ &= B \times i \times 1 \\ &= B \times qNv \ \rm[N] \end{align} \)
と計算できます。また,荷電粒子1つあたりにはたらく力(ローレンツ力)の大きさは,
\(\begin{align} f &=\displaystyle \frac{F}{N} \\ \\ &=\displaystyle \frac{B \times qNv}{N} \\ \\ &= Bqv \ \rm[N] \end{align} \)
となります。
電磁力は,磁界中を移動する電流にはたらく力であるのに対し,ローレンツ力は磁界中を移動する荷電粒子にはたらく力を表します。すなわち,荷電粒子1粒にはたらくローレンツ力を足し合わせたものが電磁力(アンペールの力)になるのです。
コイルに働く回転する力(トルク)
トルクとは?
トルクとは,回転させようとする力のことを言います。下図のように軸として1点が固定されている場合,力が働くとまっす直進できずに回転する動きになります。
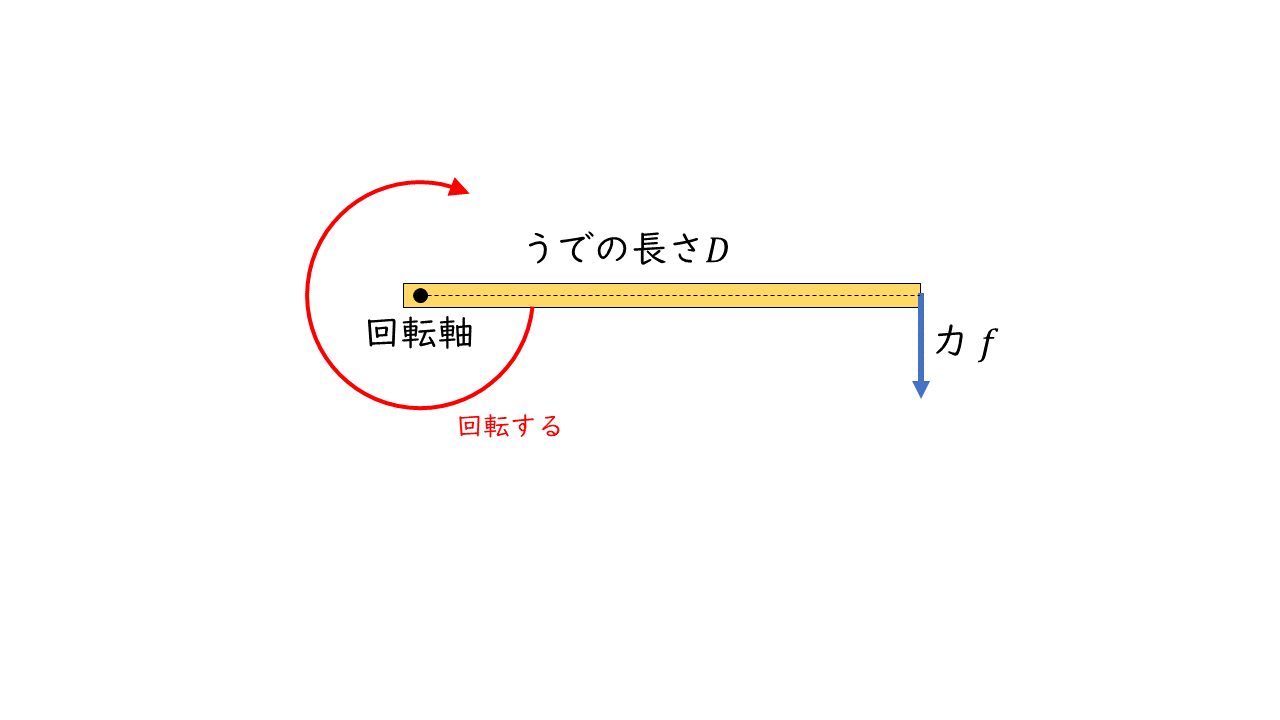
トルクは記号 \(T\) で表され,単位は \(\rm[N・m]\) ニュートンメートルを使います。
うでは回転運動をするため,うでにはたらく力の向きは常に変化します。
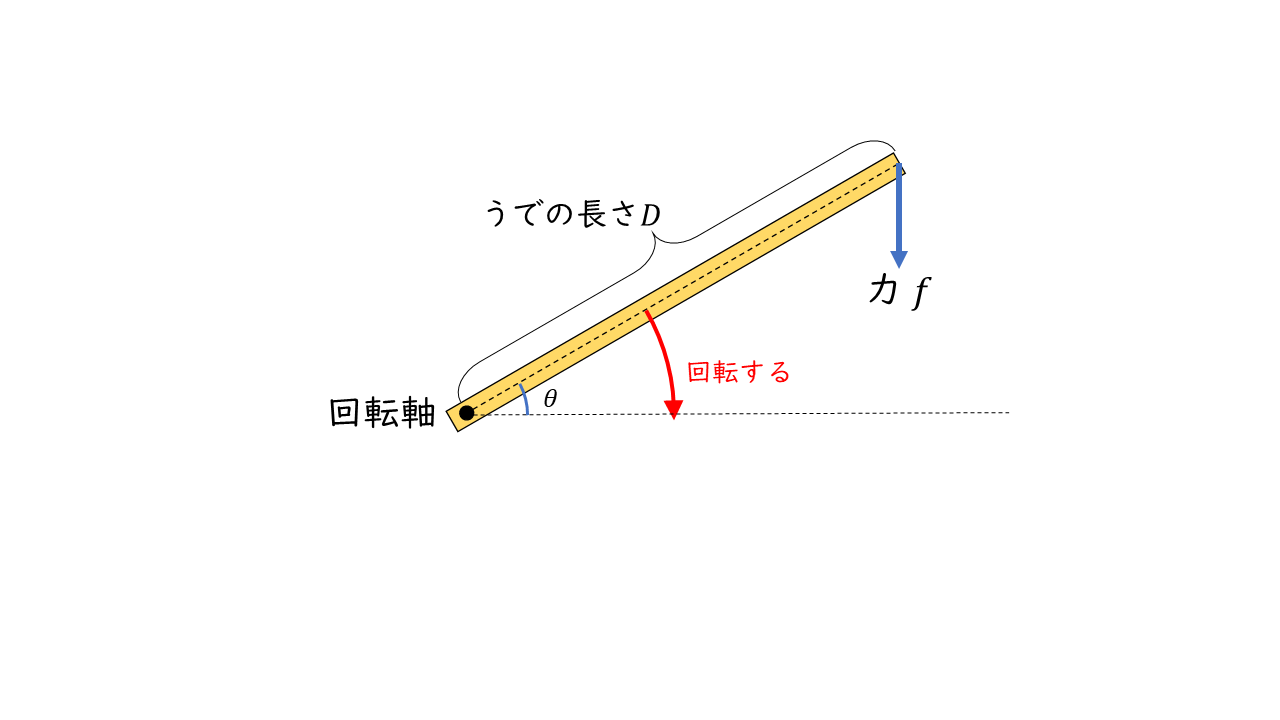
回転運動に影響を与えるのは”うで”に垂直に働く力のみです。したがって、”うで”と”うでにはたらく力”の角度が変化するためその影響を考慮すると次の式でトルクを表すことができます。
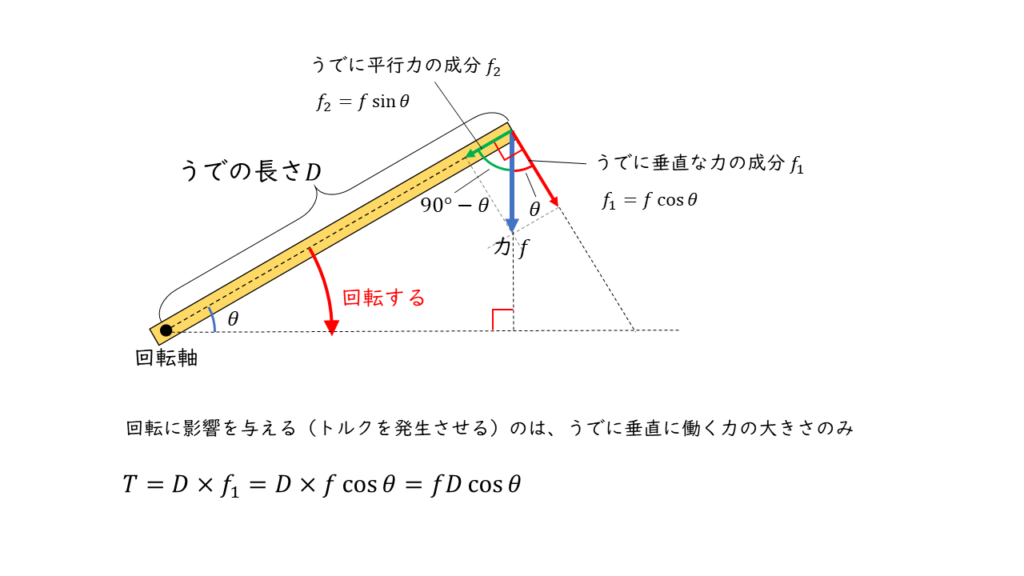
\(\begin{align} T &= D \times f_1 \\ &= D \times f \cos\theta \\ &= fD\cos \theta \end{align} \)
\(D\) :うでの長さ [m]
\(f\) :うでにはたらく力 [N]
\(f_1\) :うでに垂直にはたらく力の成分 [N]
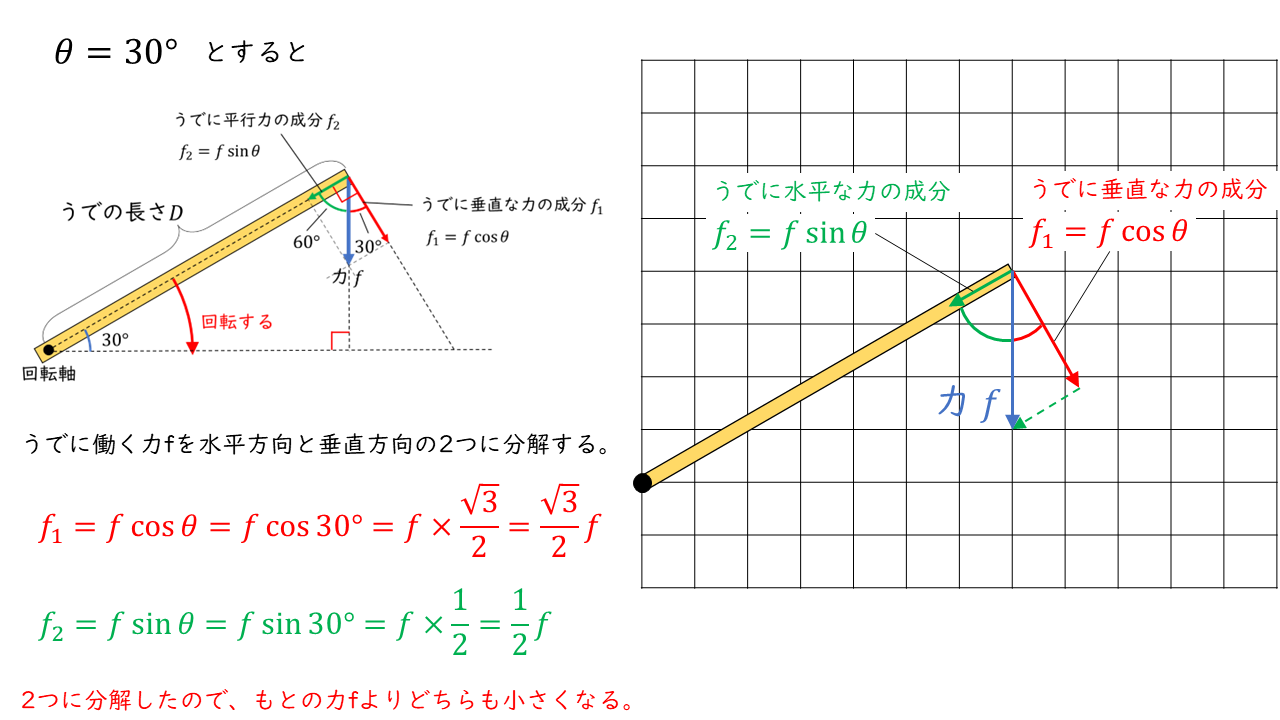
例)うでが \(30°\) の角度にあるとき
トルクの応用
電磁力による回転力(トルク)を利用したものに電動機(モーター)があります。その基本となる原理は次のようになります。
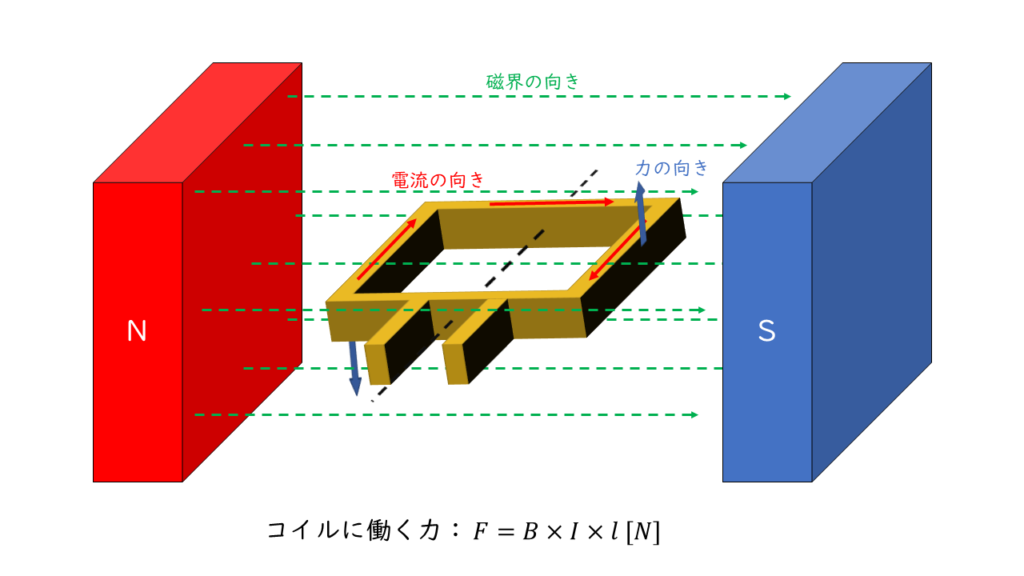
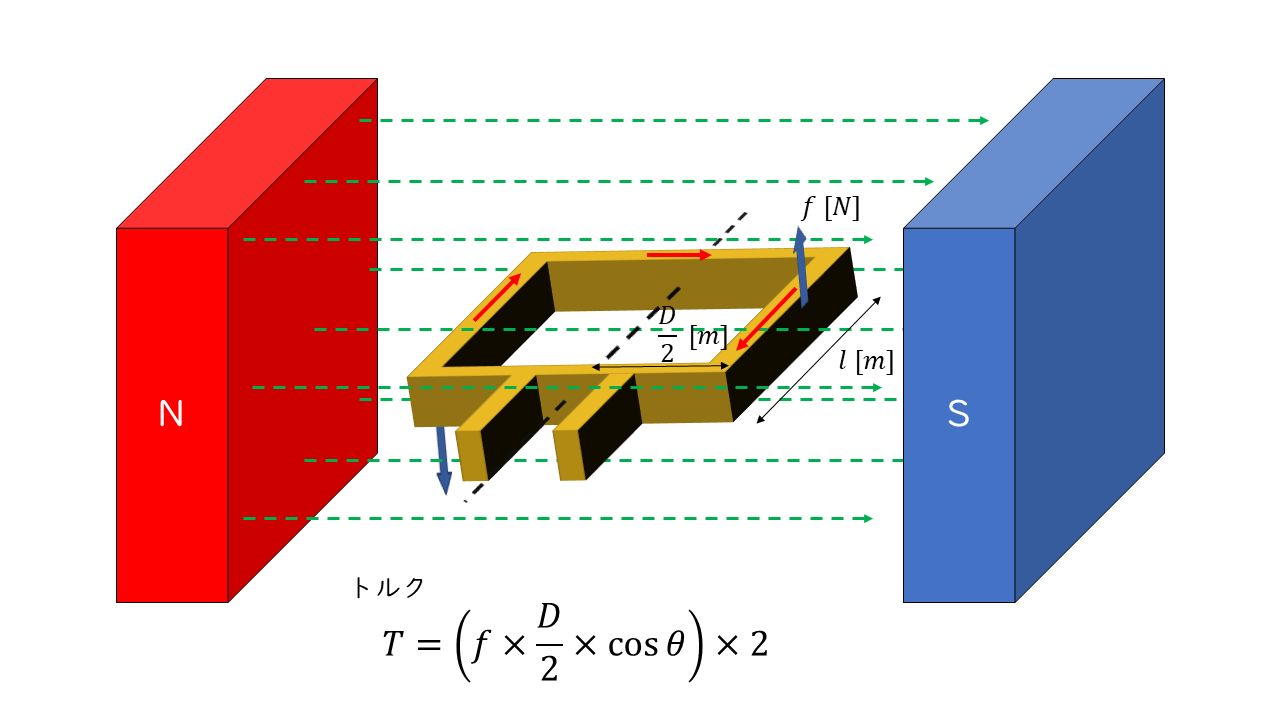
回転軸を中心に考え、回転軸からコイルの端までの長さ(うでの長さ)を\(\frac{D}{2}\),導体の長さ(コイルの奥行)を\(l [m]\)、磁束密度(磁界の強さ)を\(B [T]\)、電流の大きさを\(I [A]\)とするとコイルにはたらくトルクの大きさは
\(\begin{align} T &= F \times D \cos\theta \\ &= B I l \times D \cos\theta \ \rm [N・m] \end{align} \)








コメント