- 磁気回路とは何か
- 磁気回路のオームの法則
- 磁気抵抗の合成
- エアギャップ(空隙)のある磁気回路の計算方法
- ヒステリシス曲線

磁気回路は、電動機や変圧器の分野の基礎にあたります。
理論を制する者が「電験を制す」です!
1つずつ意味を理解して次に進んでいきましょう。
磁気回路とは
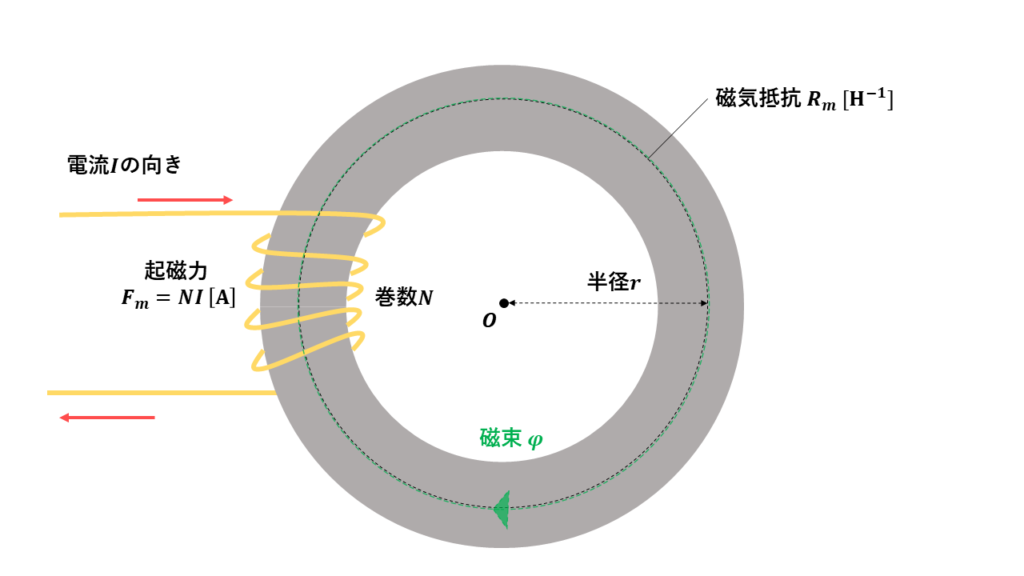
上図のように環状鉄心に被覆された導体を巻き付け、導体に電流を流すと磁束(磁界)が発生します。発生する磁束のほとんどは、磁気(磁力線)の通りやすい鉄心の内部に集中し、鉄心の外側にはあまり磁束が発生しません。
このような、磁束の通り道を磁気回路(磁路)といいます。
起磁力
磁束を発生させる元になる力のことを起磁力と呼びます。
記号 \(F_m\) , 単位 \([A]\)アンペア
で表されます。起磁力は、コイルの巻き数\(N\)と電流\(I [A]\)に比例します。
$$F_m = N \times I\ [A]$$
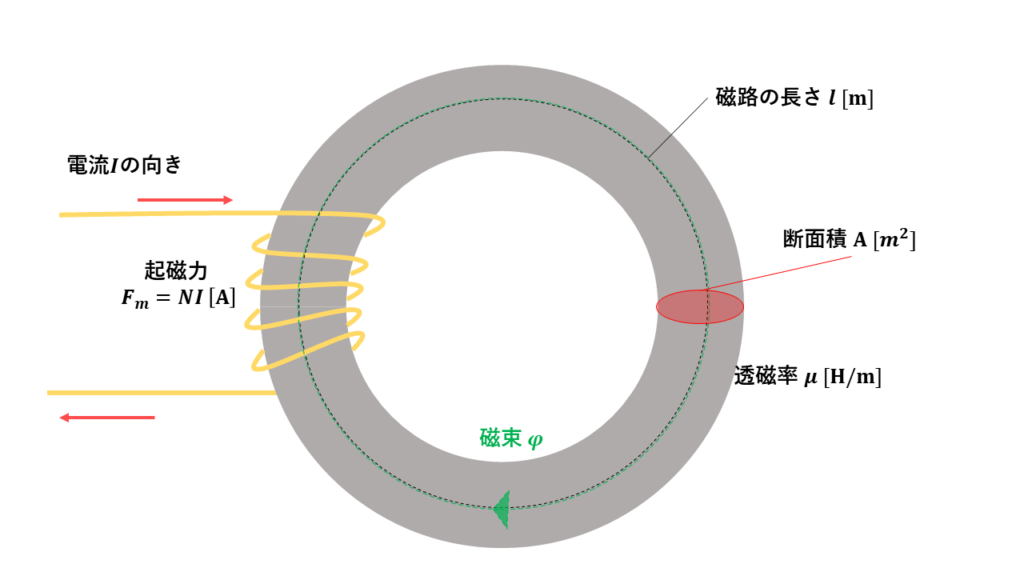
磁気抵抗
磁束\(\phi [Wb]\)の通りやすさを妨げるものを磁気抵抗と呼びます。エアギャップなども磁気抵抗に該当します。
記号:\(R_m\) , 単位:\([H^{-1}]\)毎ヘンリー
で表されます。磁束\(\ \phi [Wb]\)は、鉄心の断面積が大きいほど通りやすく(比例)、磁路の長さ\(\ l [m]\)が長いほど通りにくくなります(反比例)。
$$R_m = \frac{l}{\mu \times A} \ [H^{-1}]$$
磁気回路のオームの法則
磁気回路は電気回路ととてもよく似た要素を持っているため、磁気回路のオームの法則が存在します。
$$\begin{align} R_m & = \frac{NI}{\phi} \\ 磁気抵抗[H^{-1}] & = \frac{起磁力 [A]}{磁束[Wb]} \end{align}$$
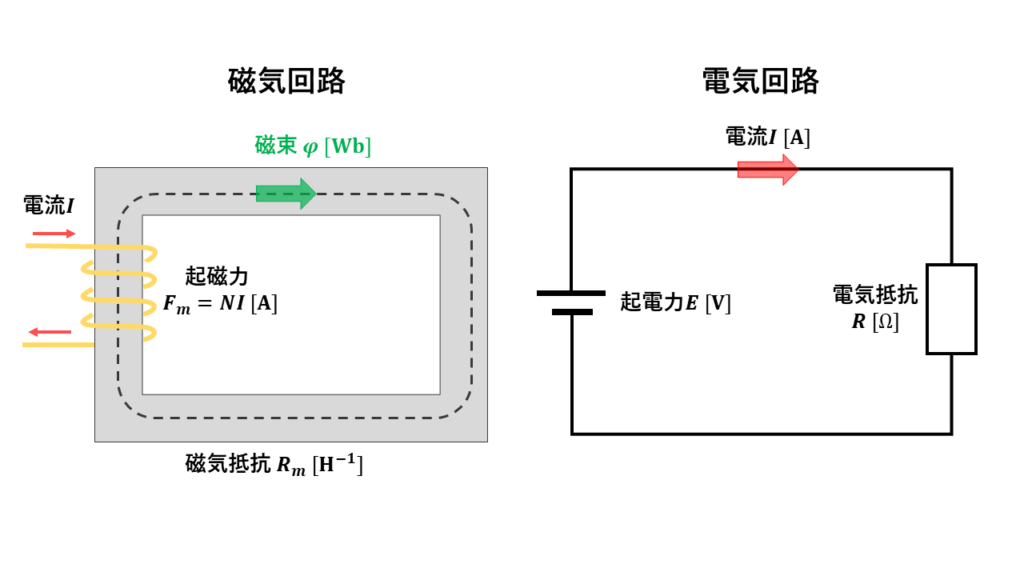
| 磁気回路のオームの法則 $$ \phi = \frac{NI}{R_m} [Wb] $$ | 電気回路のオームの法則 $$ I = \frac{E}{R} [A] $$ |
| 起磁力 \(NI [A]\) | 起電力 \(E [V]\) |
| 磁束 \(\phi [Wb]\) | 電流 \(I [A]\) |
| 磁気抵抗 \(R_m = \frac{l}{\mu A} [H^{-1}]\) | 電気抵抗 \(R=\frac{l}{\sigma A} [\Omega]\) |
| 透磁率 \(\mu [H/m]\) | 導電率 \(\sigma [S/m]\) |
磁気抵抗の合成

磁気回路が電気回路と同じに考えられるように、
抵抗についても、電気抵抗と同じに考えられるよ!
直列接続の場合
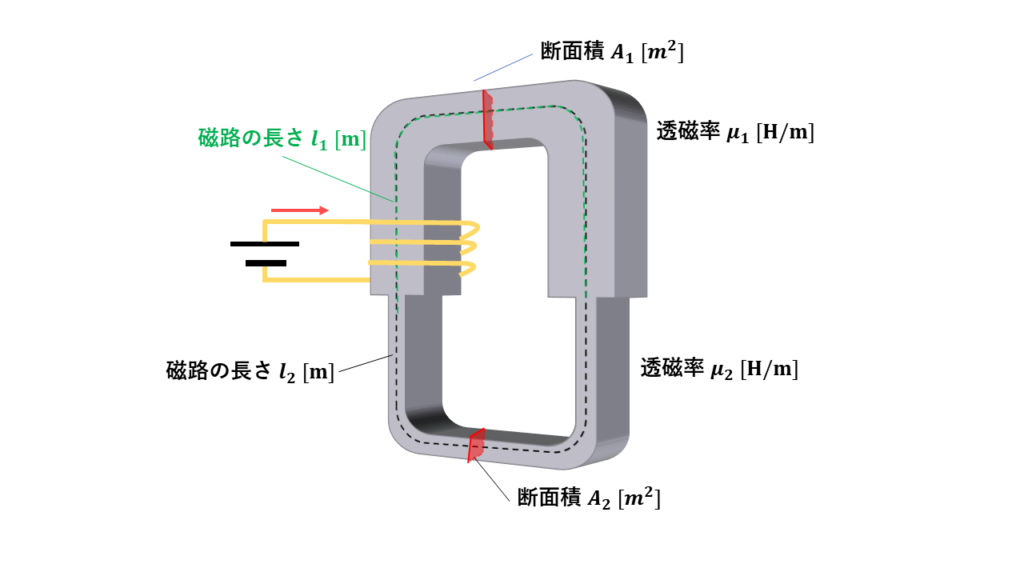
透磁率や断面積、磁路の長さが異なる物質が直接つながれた磁気回路では、2つの異なる磁気抵抗が直列に接続されていると考えます。
この時の計算方法は、電気回路での直列接続された電気抵抗の大きさの計算と同じ方法です。
$$\displaystyle R_{m0} = R_{m1}+R_{m2}
=\frac{l_1}{\mu_1 A_1} + \frac{l_2}{\mu_2 A_2}$$
並列接続の場合
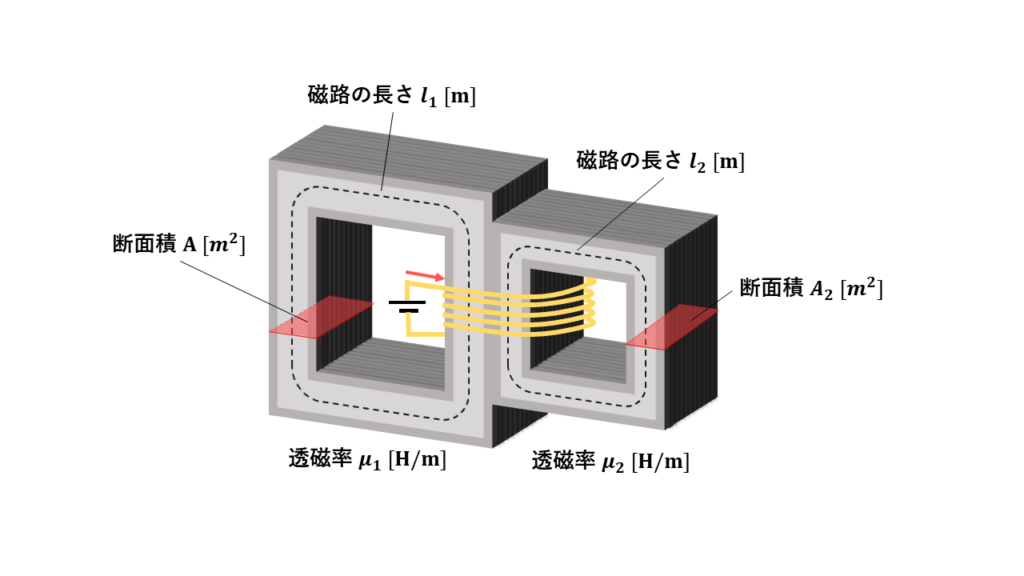
透磁率や断面積、磁路の長さが異なる物質が並べられた磁気回路は、2つの磁気抵抗が並列接続されていると考えます。
この時は、並列に接続された電気抵抗と同じ計算方法になります。
$$\displaystyle R_{m0} =\frac{1}{ \frac{1}{R_{m1}} + \frac{1}{R_{m2}}}
= \frac{1}{\frac{\mu_1 A_1}{l_1} + \frac{\mu_2 A_2}{l_2}}$$
透磁率・比透磁率
比透磁率とは、真空の透磁率を基準としたとき、対象とする物質の透磁率が真空中の透磁率の何倍になるかを表した比のこと。
比透磁率 \(\mu_r = \frac{\mu}{\mu_0}\)
何倍になるかを表すものなので、単位はありません。
また、比透磁率の大きさが1よりも大きい物質(鉄、ニッケルなど)を強磁性体、比透磁率がほぼ1(1よりわずかに大きい)の物質を常磁性体、比透磁率が1より小さい物質を反磁性体と呼びます。
エアギャップのある磁気回路
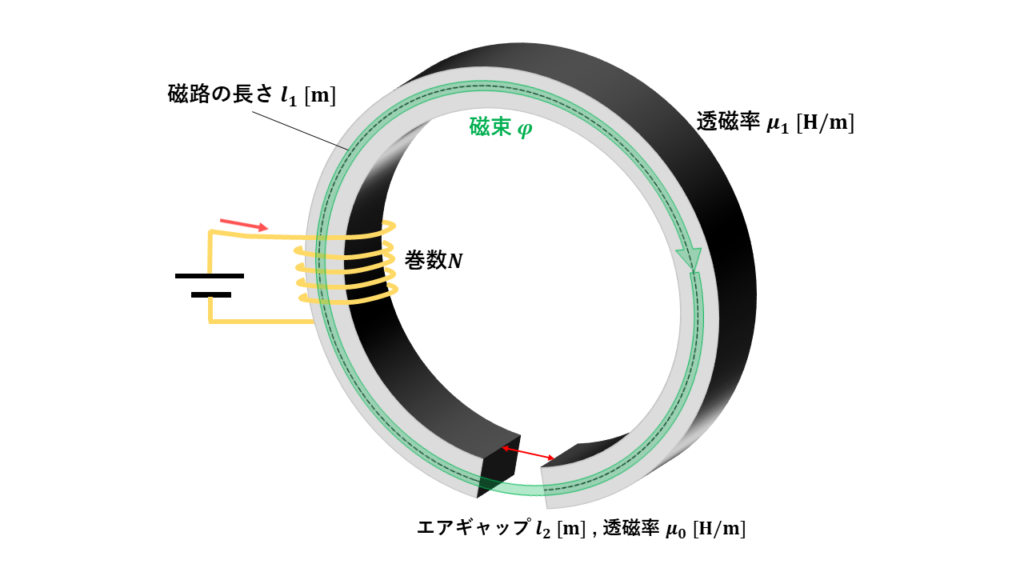
エアギャップ(空隙)とは、上図のように鉄心に存在する隙間(鉄心が途切れた部分)のことを言いさしています。これを磁気回路として表すと次のようになります。
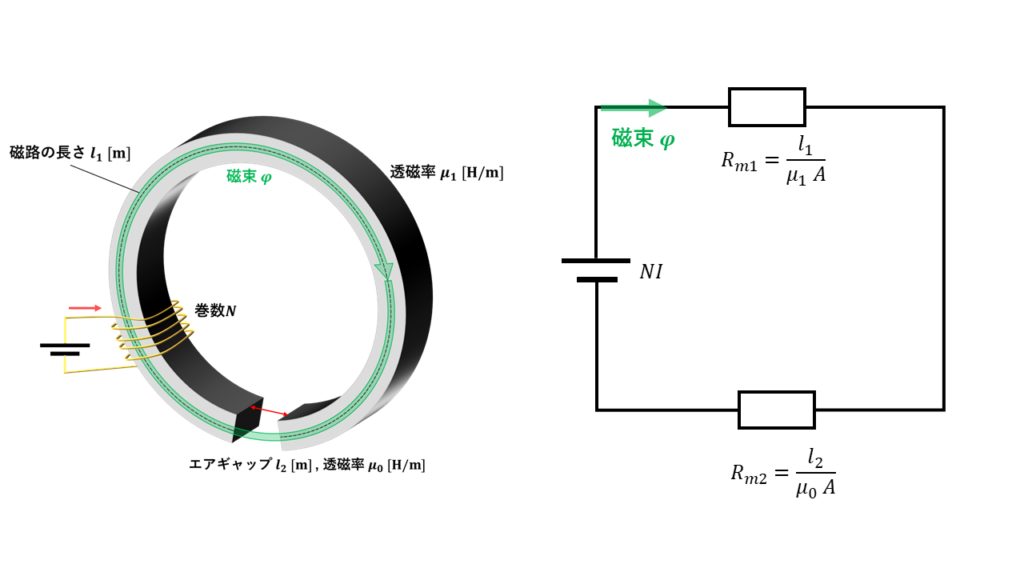
エアギャップのある磁気回路では、鉄心の磁気抵抗\(R_{m1}\)とエアギャップの磁気抵抗\(R_{m2}\)は直列に接続されていると考えます。
ヒステリシス曲線
磁気飽和とB-H曲線
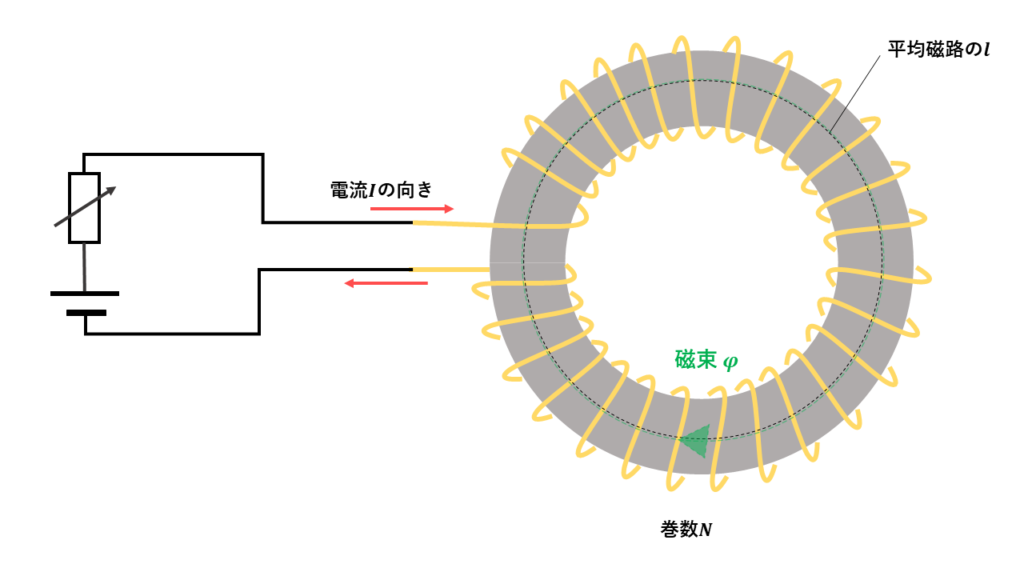
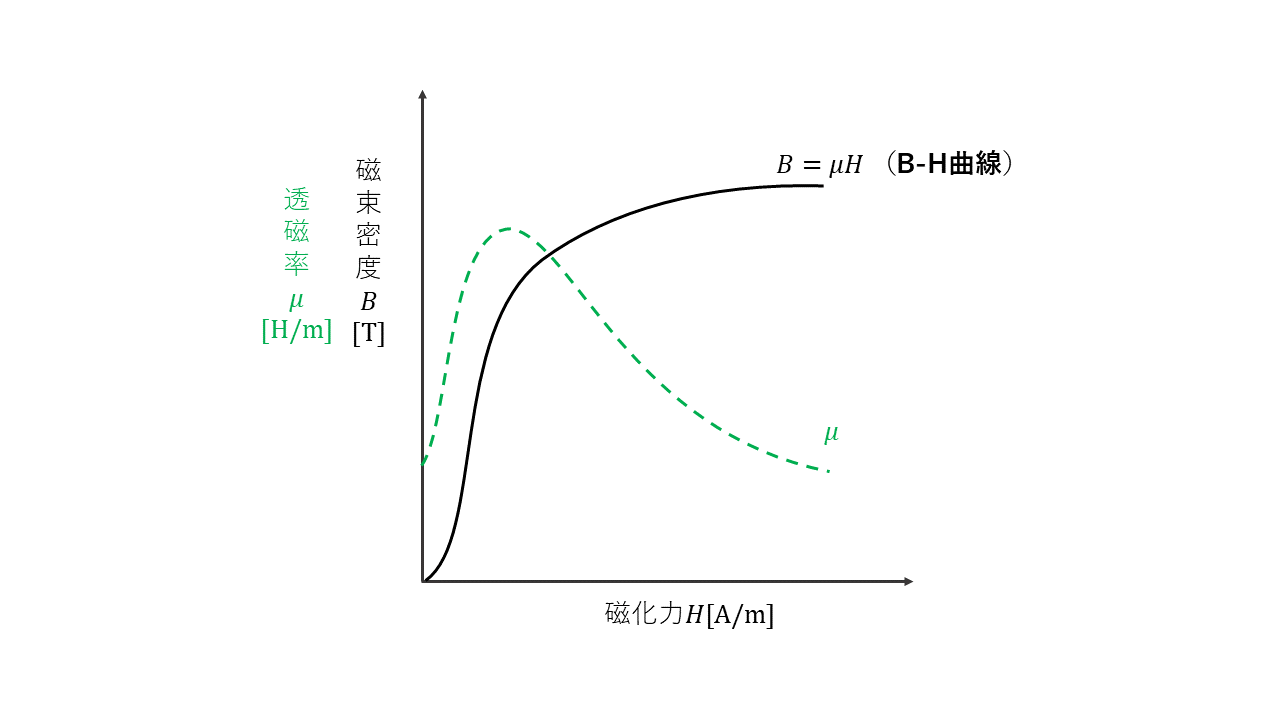
環状鉄心に巻かれているコイルに流す電流を徐々に大きくすると、電流の作る磁界が大きくなり、鉄心は徐々に磁気(磁界強さ)を帯びていきます。この時、鉄心に加えた磁界の大きさ\(H\) [A/m]を磁化力といいます。
縦軸に磁束密度\(B\) [T]、横軸に磁化力\(H\) [A/m]をとって両者の関係を示したグラフを\(B\)-\(H\)曲線といいます。
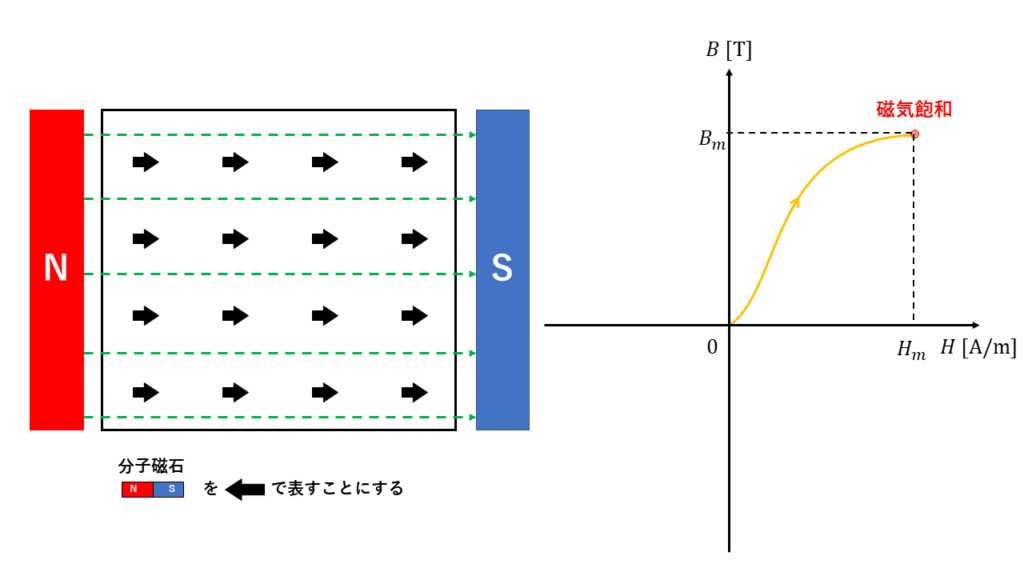
磁束密度\(B\) [T]は、初めは磁化力\(H\) [A/m]に比例しますが、ある値を境にほとんど増えなくなります。これを磁気飽和といいます。
ヒステリシス曲線

磁気飽和の概念を頭に入れながら、
ヒステリシス曲線がどのような手順で書かれていくのか見ていこう!
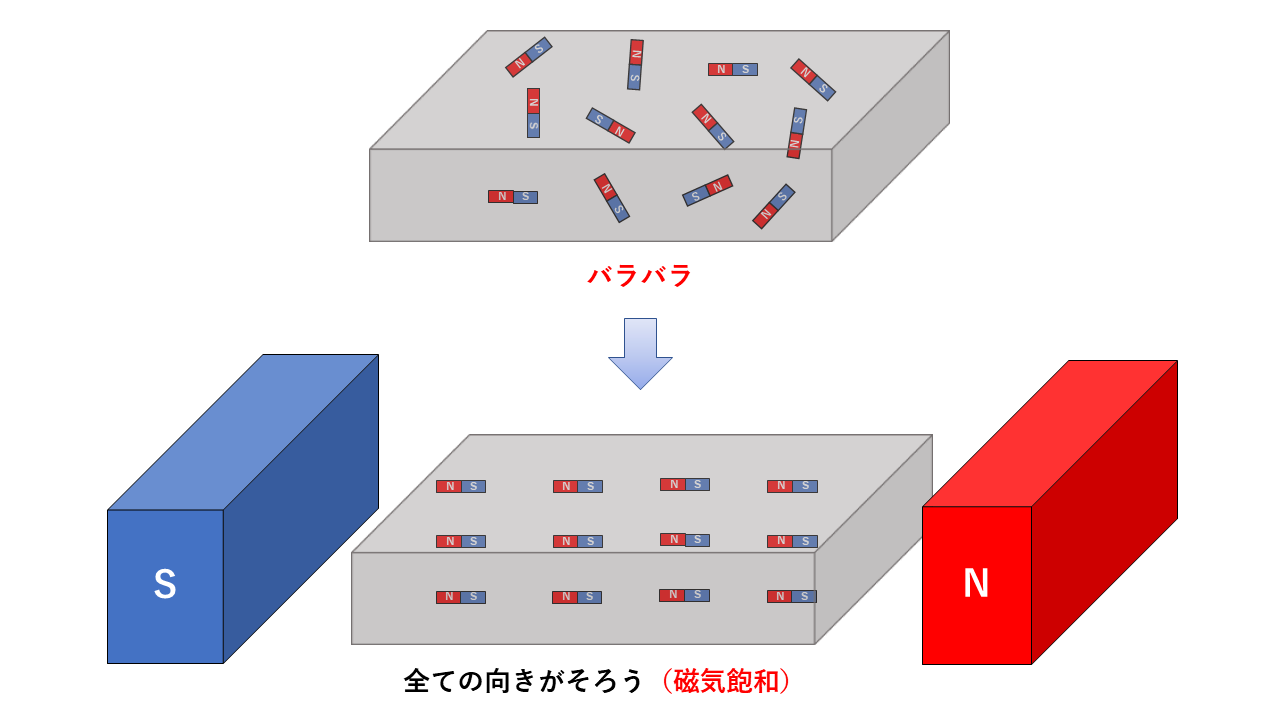
鉄を構成する原子の集まりは1粒1粒が磁石のように磁気を帯びていますが、非常に弱くそれぞれの向きもバラバラなため、鉄の塊で見ると磁気を帯びていないように見えます。
ところが、外部から磁化力\(H\)を加えると、磁気飽和が起こる\(H_{m}\)まで徐々に磁化していきます。
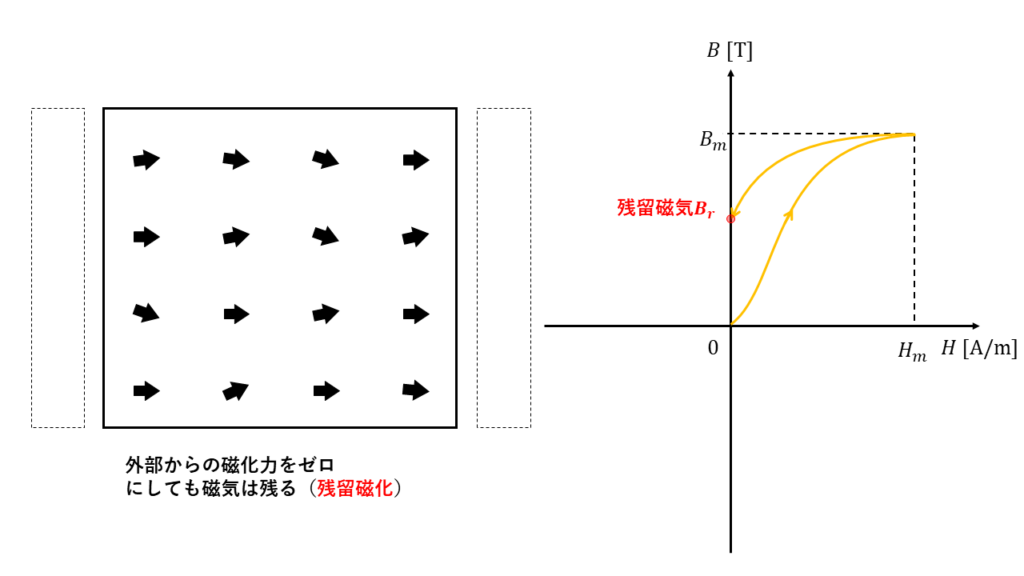
次に、磁化力を徐々に弱めていき、ゼロにします。外部からの磁化力がゼロになっても、鉄の磁束密度\(B\)はわずかに残ります。この時の磁束密度\(B_{r} [T]\)を残留磁気といいます。

クリップに何度も磁石をこすりつけると、
クリップが磁石になるのと同じことだね
残留磁気をゼロにするためには、初めに加えた磁化力とは逆向きの磁化力を加える必要があります。磁化された状態を保つことができる限界の磁化力を保持力\(H_c\)といいます。
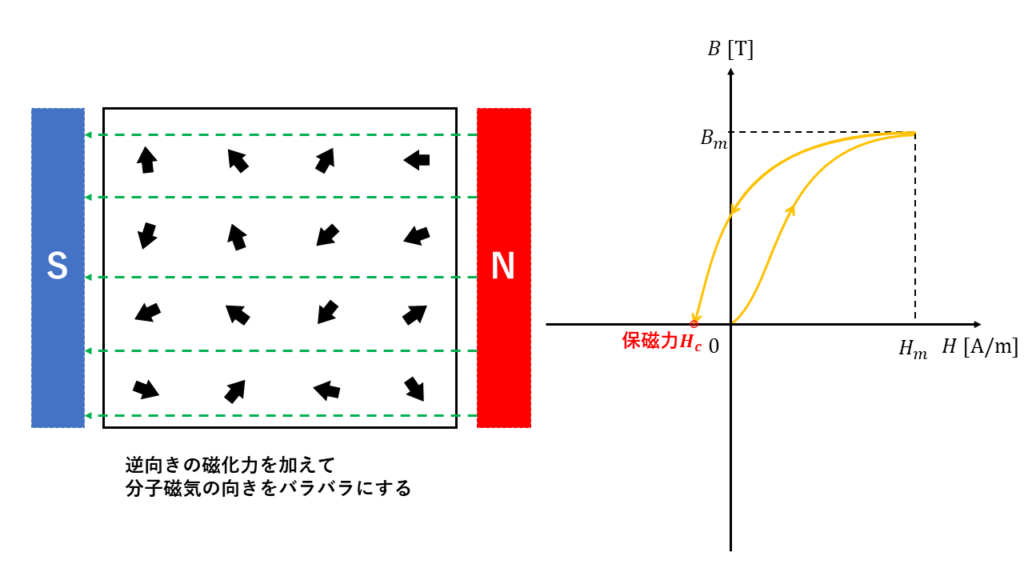
逆向きの磁化力をさらに強くしていくと、今度ははじめとは逆向きの方向に分子磁石がそろい、再び磁気飽和が起こります。
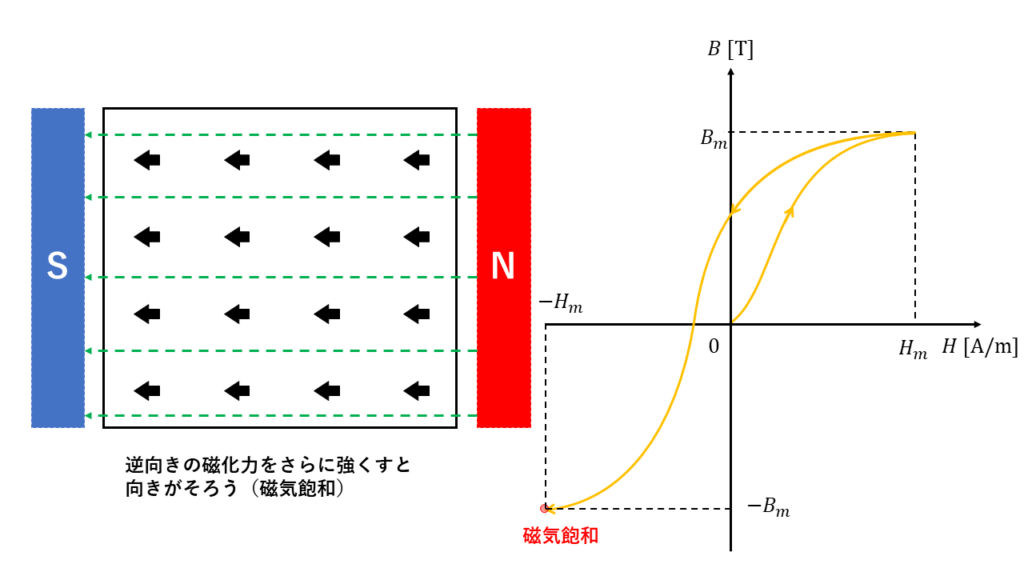
これまでと同様に、磁化力がゼロとなるまで弱め、さらに逆向きの磁化力を徐々に加え磁気飽和させるという工程を繰り返すと\(B-H\)曲線では次のような形を描きます。
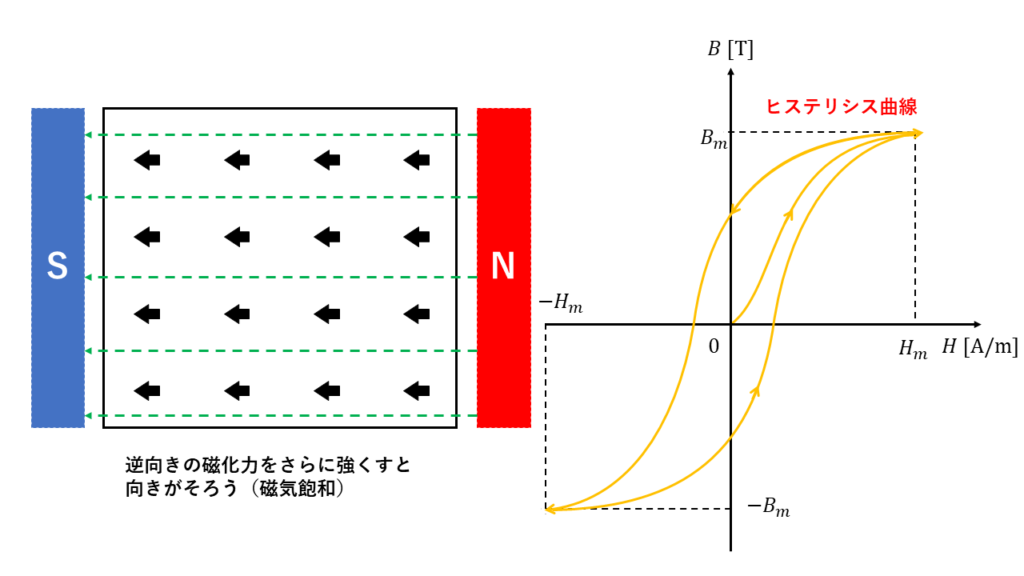
この1周りする閉じた曲線のことをヒステリシス曲線(ヒステリシスループ)と呼びます。
また、ヒステリシス損とは、分子磁石が方向を変える際に回転することで摩擦が生じ、熱となって電気エネルギーの一部を消費することを言います。
まとめ

今回は、変圧器や電動機の学習にもつながる磁気回路とヒステリシス曲線について解説しました。








コメント