整流回路とは
整流回路とは、交流電力を直流電力に変換する回路を言います。
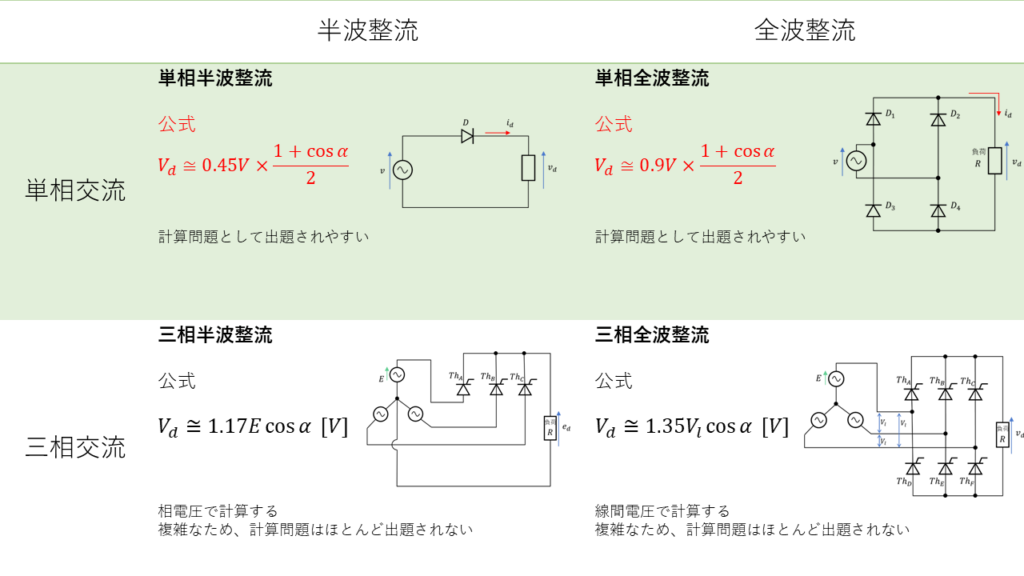
整流回路には、電源の種類が「単相交流か」,「三相交流か」と、整流する交流波が「半分の波か」,「全ての波か」で合わせて4つの組み合わせがあります。
単相半波整流
ダイオード整流
ダイオードを1つ使用することで交流を直流に変換することできます。これは、ダイオードの逆方向に電圧をかけても電流を流さない性質を利用した回路です。
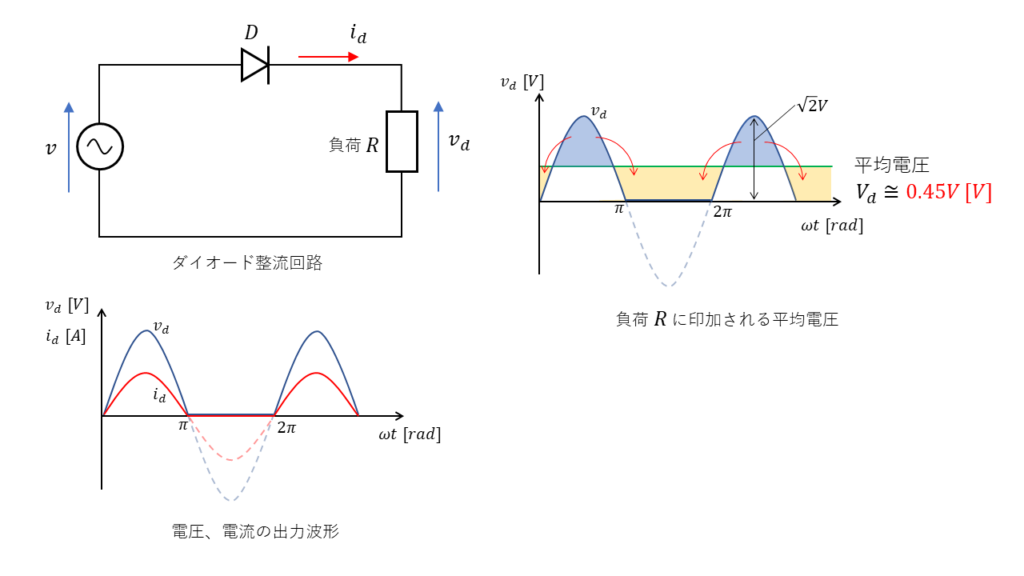
整流された\(v_d\)や\(i_d\)をグラフ化すると直線ではなく波打った形(脈流)になりますが、向きが常に正方向であるため直流と考えることができます。
ダイオードによって直流に変換され、負荷Rへ印加される直流電圧の平均値は\(V_d \ \rm[V]\)は、交流電圧の実効値\(V\ \rm[V]\)を使って次の様に表すことができます。
$$ V_d = 0.45V \ \rm [V] $$
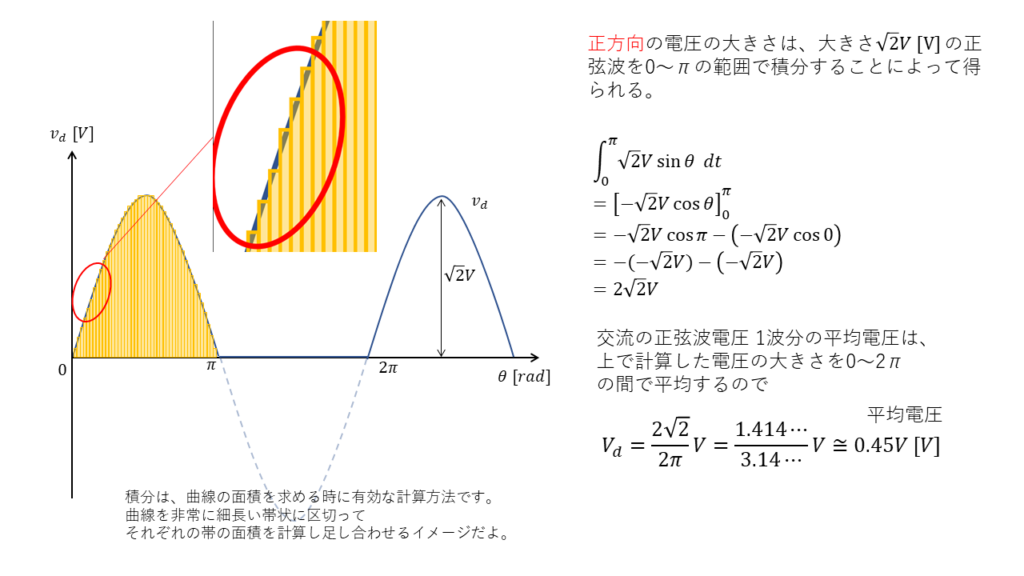
公式の導出には積分を使用します。電験3種では公式の導出まで問う問題はないため、計算が苦手という方は公式の暗記だけでも大丈夫です。
サイリスタ整流
サイリスタもダイオードと同様に、逆方向の電圧が印加された場合は電流を通しません。ダイオードとの違いは、ゲートに信号(パルス電流)を入力することで電流の流れるタイミングを決めることができる(制御できる)点です。
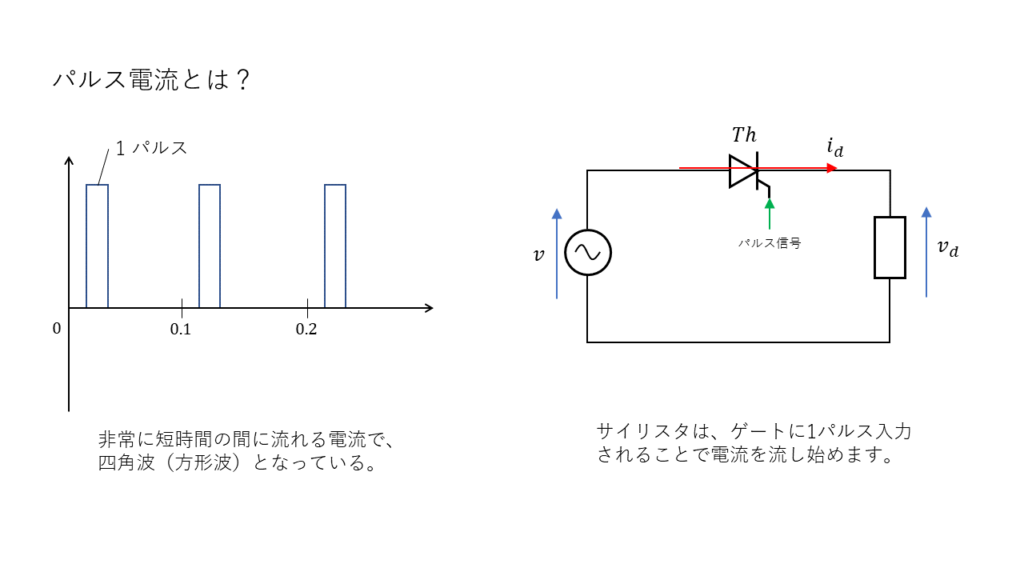
サイリスタ整流回路では、位相角\(\alpha \ \rm [rad] \)のところでサイリスタのゲートにパルス電流を流すと、その瞬間から電流\( i \ \rm [A] \)を流し、抵抗\(R\)に電圧\( v _d \ \rm [V] \)が印加されます。この位相角\(\alpha \ \rm [rad] \)のことを制御角と呼びます。
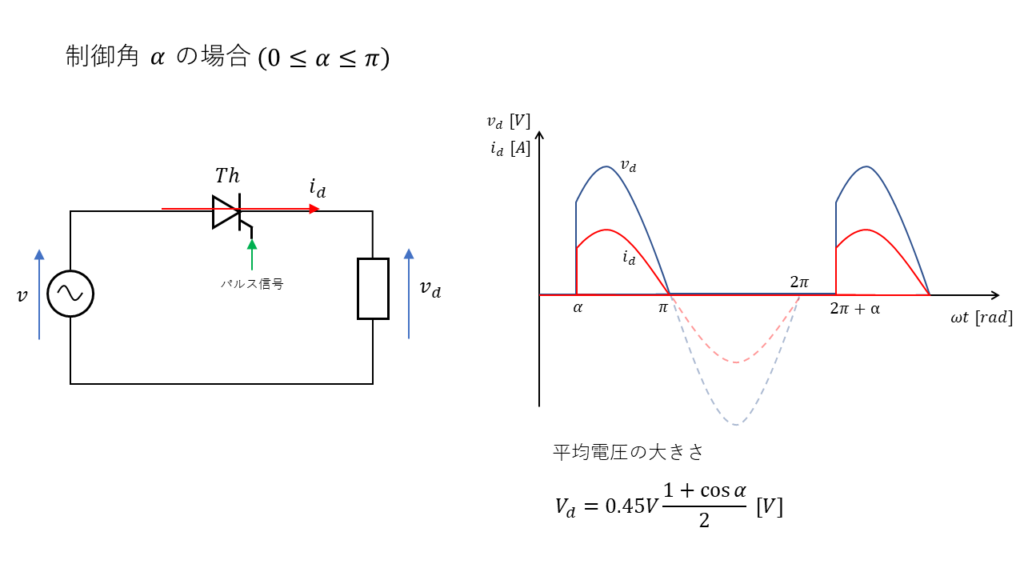
サイリスタ整流回路における負荷Rに印加される直流平均電圧\(V_d \ \rm[V]\)の大きさも、ダイオード整流回路の時と同様に交流電圧の実効値\(V \ \rm[V]\)を使って表すことができます。
$$ V_d = 0.45V \times \frac{1+\cos \alpha}{2} $$
サイリスタ整流回路は制御角\(\alpha\)~\(\pi\)の範囲での出力になるため、ダイオード整流回路で積分の時に0とした値を\(\alpha\)に置き換えて計算すれば平均電圧の式が得られます。

単相全波整流
ダイオード整流回路
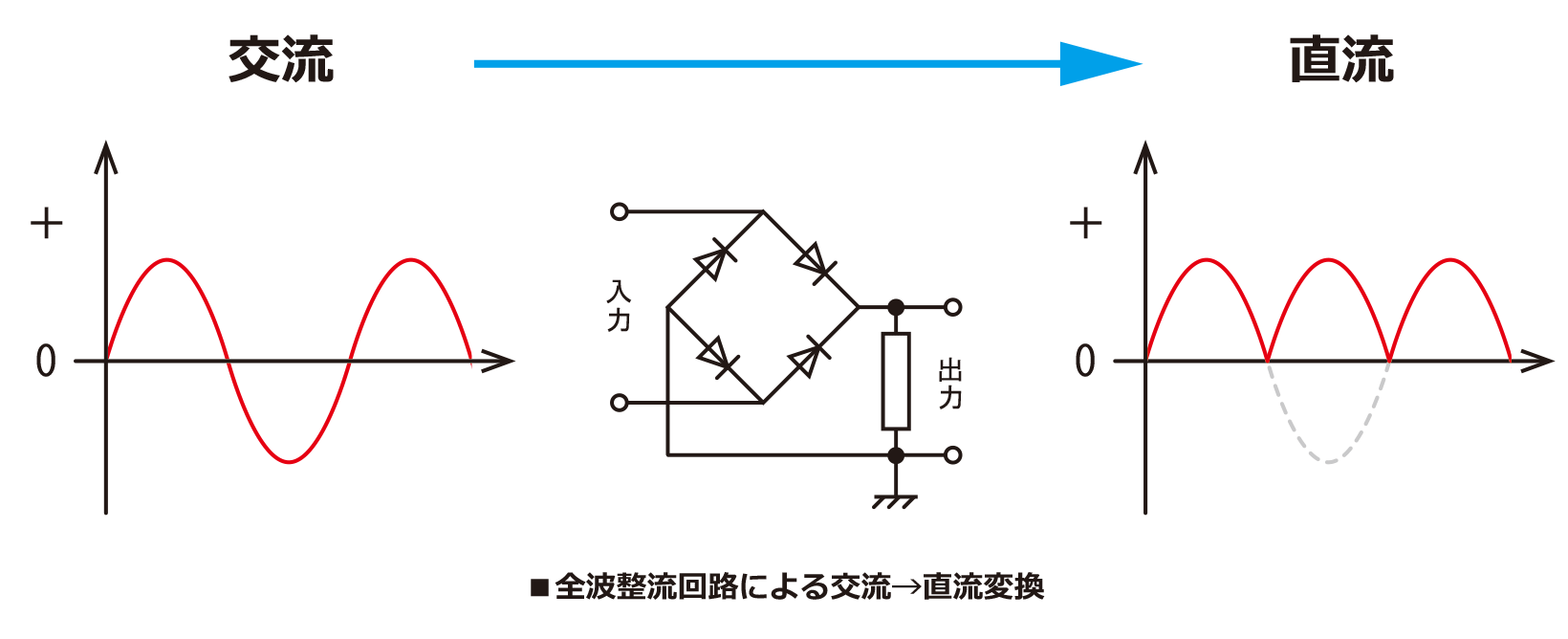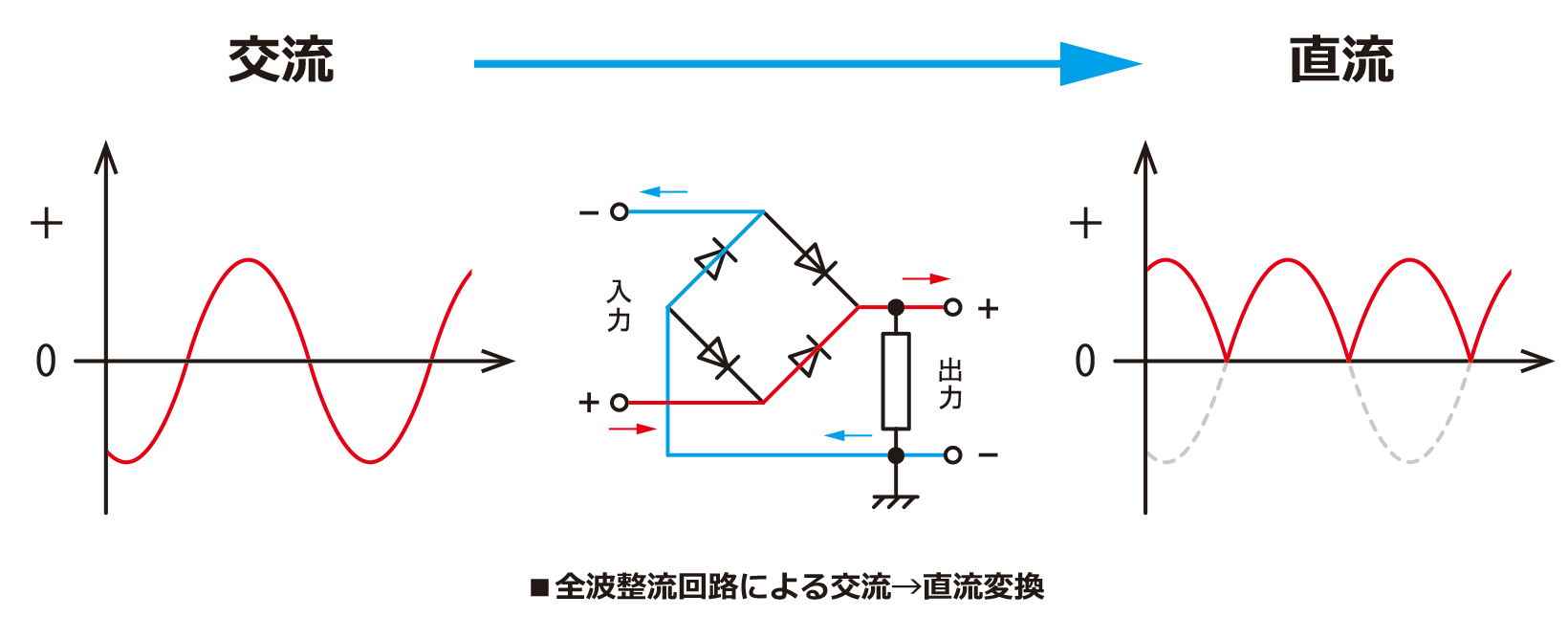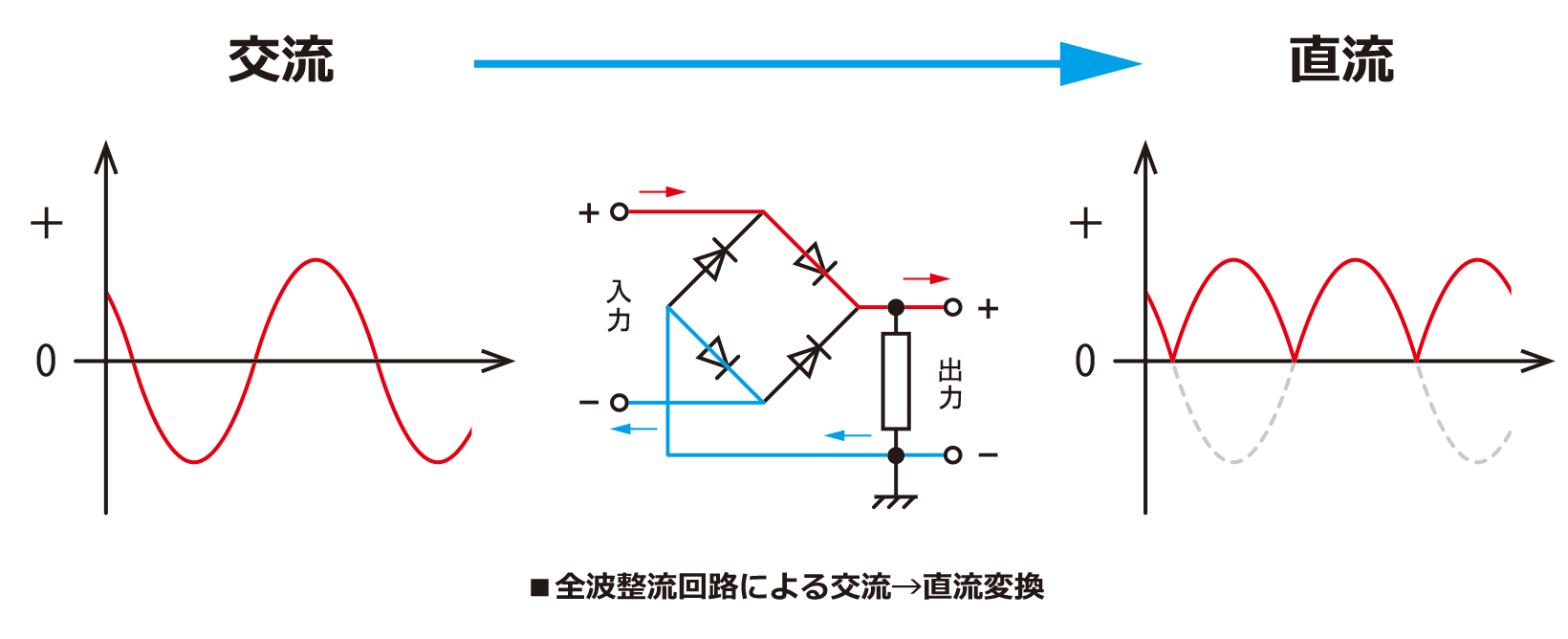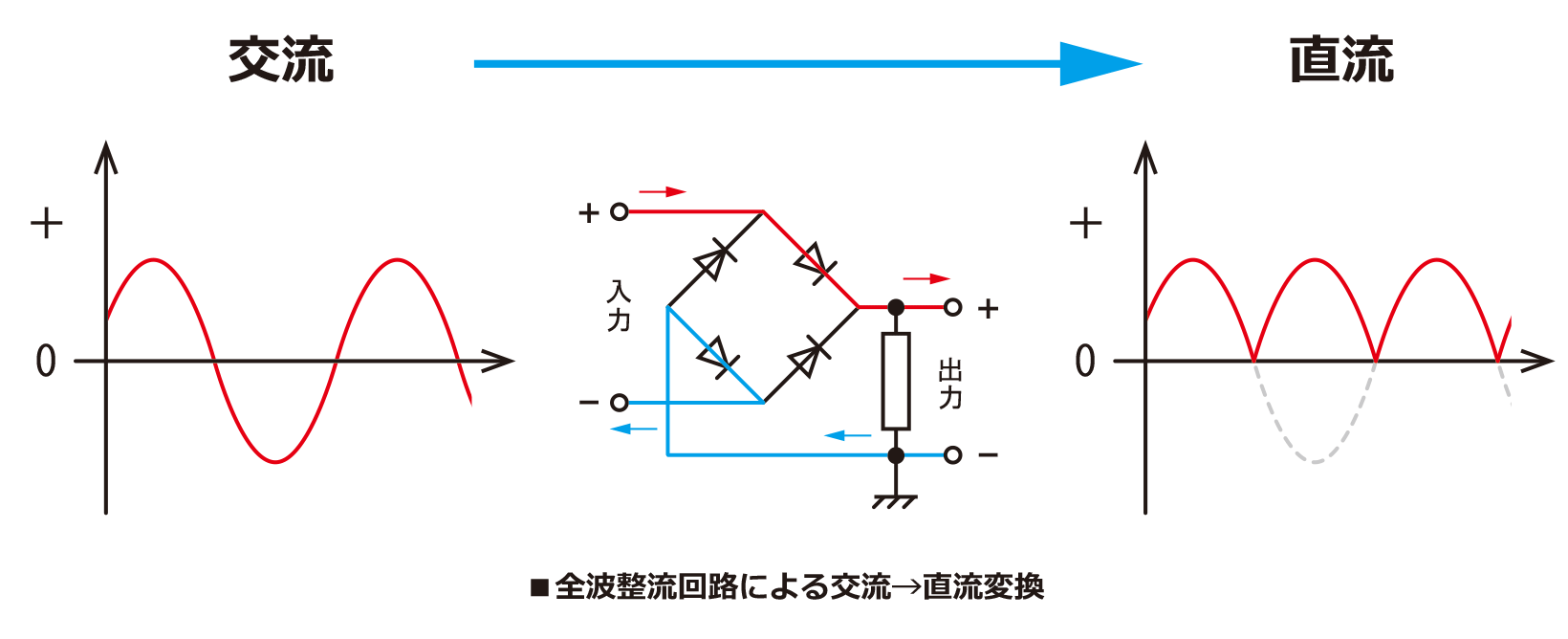
ダイオードを4つ使用して図5の様に回路を作ることで、交流の向きがが変わっても負荷Rに流れる電流の向きは常に一定になります。
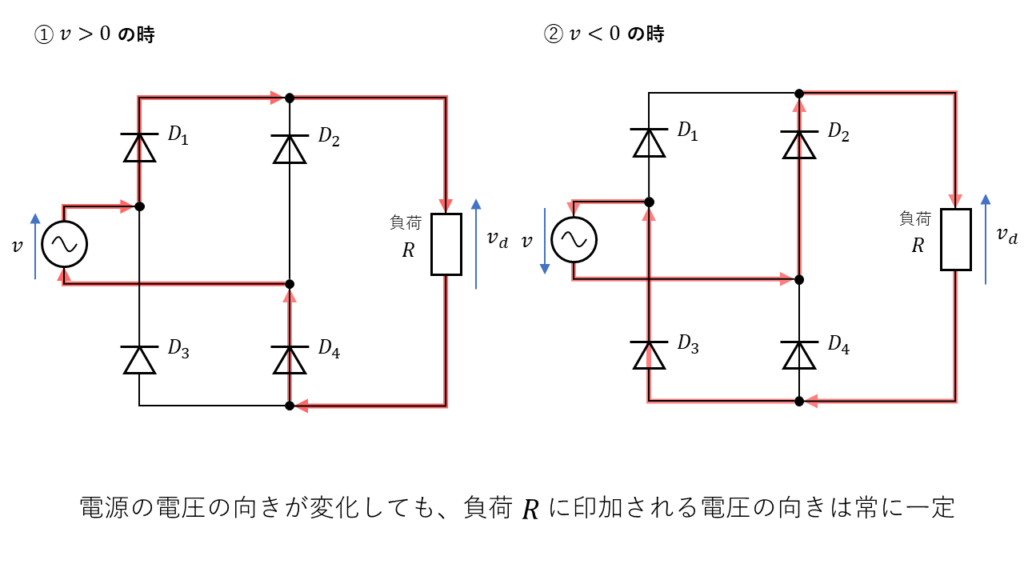
また、理論科目で学習したブリッジ回路の形で記載されることもあります。
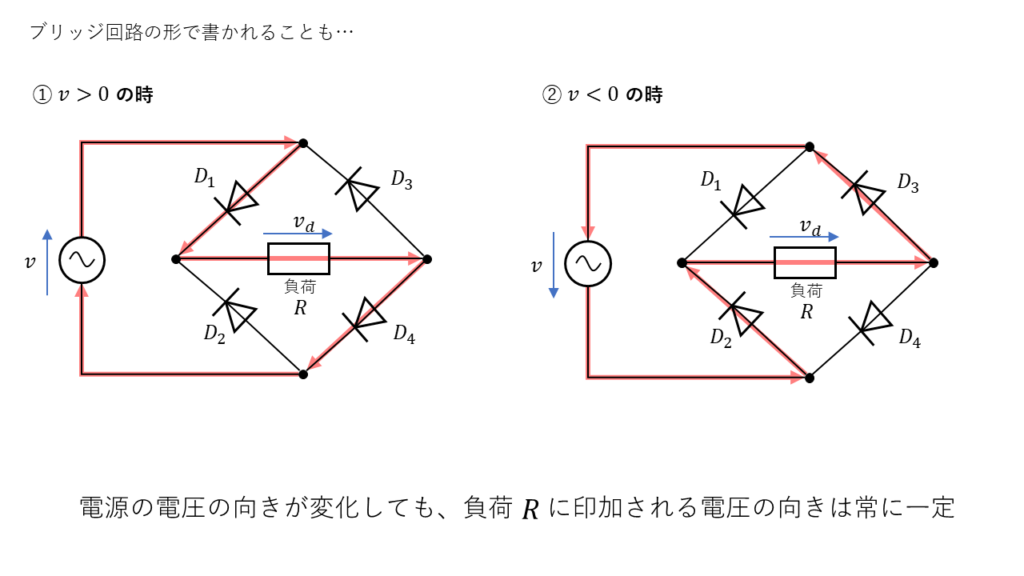
図5、図6ともに形が異なるだけで同じ回路を表しています。そのため、電源のため交流電圧の向くが変化しても負荷Rに印加される電圧は常に一定の向きになります。ダイオード全波整流回路によって整流された電圧、電流の出力波形は図7の様になります。
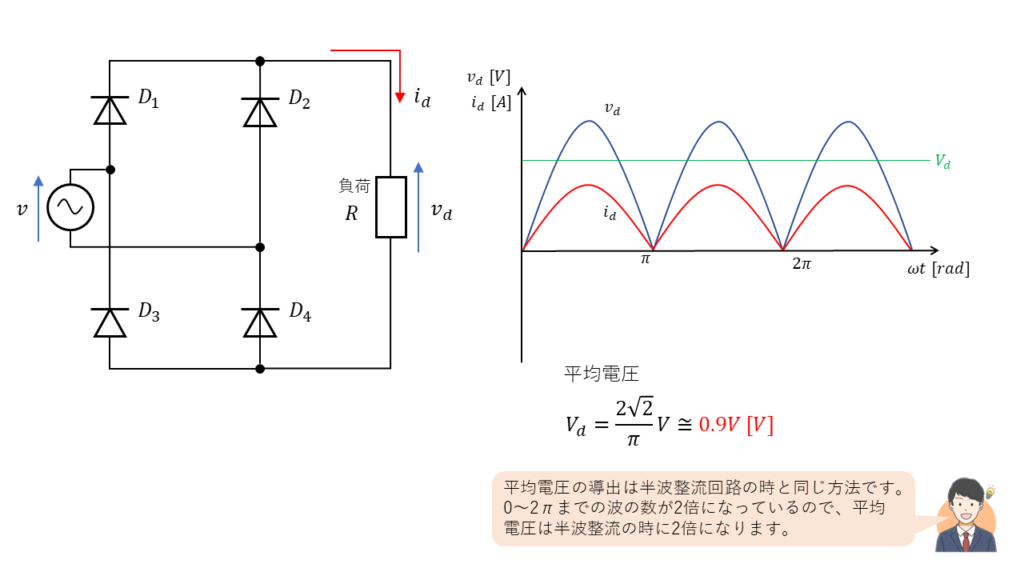
(図7 ダイオード全波整流回路の電流、電圧出力波形)
全波整流回路では、全ての波を整流するため\(0\)~\(2\pi \)間の波の数が、半波整流の時の2倍になっています。そのため、直流出力電圧の平均電圧の値も半波整流の2倍になります。
サイリスタ整流回路
ダイオードの代わりにサイリスタを用いても交流全波整流が可能です。
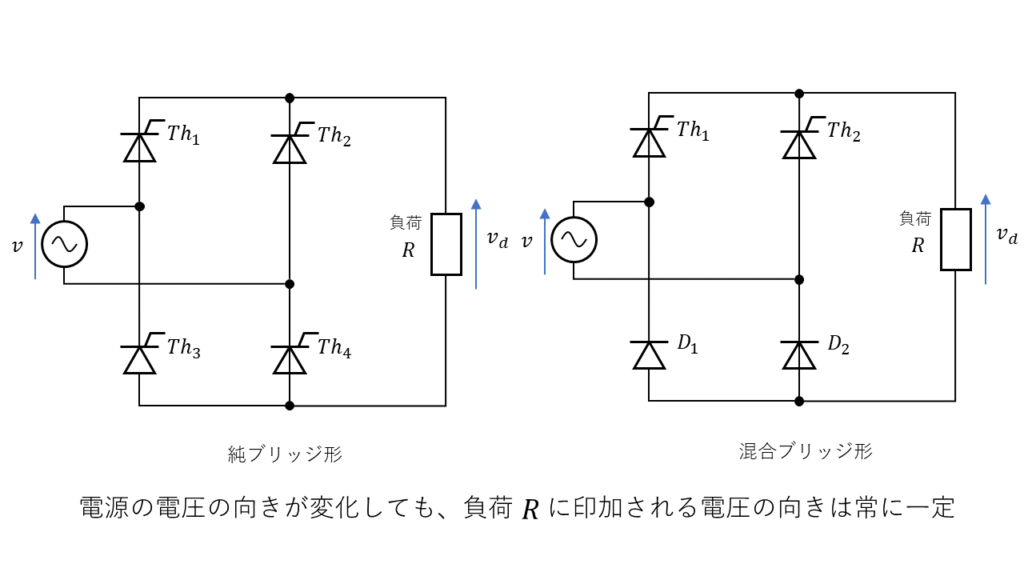
サイリスタ整流回路では4つ全てサイリスタで構成される純ブリッジ回路とサイリスタ2つ、ダイオード2つで構成される混合ブリッジ回路の2パターンがあります。電験3種では、主に純ブリッジ回路が出題されます。
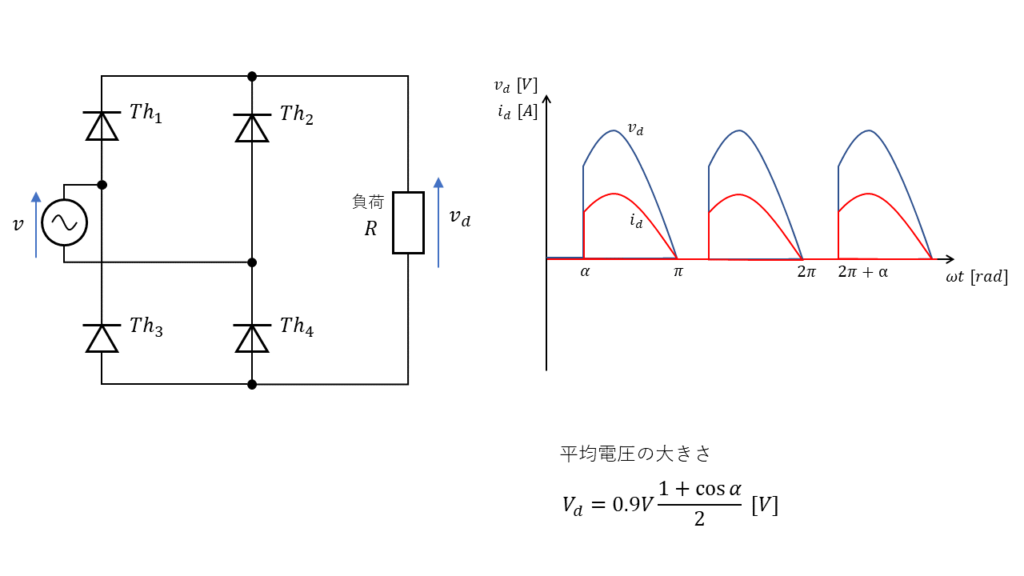
純ブリッジ回路の出力波形は図10のような形になります。この時の出力平均電圧の公式は電源電圧\(V \ \rm[V]\)と制御角\(\alpha\)を用いて次の様に表すことができます。
$$ V_d = 0.9V \times \frac{1+\cos \alpha}{2} $$
単相整流のまとめ
単相半波整流の平均電圧 \(V_d \ = \ 0.45V \times \frac{1+\cos \alpha }{2} \ \rm[V] \)
\( \alpha = 0\)の時はダイオード整流の値となる
単相全波整流の平均電圧 \(V_d \ = \ 0.9V \times \frac{1+\cos \alpha }{2} \ \rm[V]\)
\( \alpha = 0\)の時はダイオード整流の値となる
単相半波整流の平均電圧 \(V_d \ = \ 0.45V \times \displaystyle \frac{1+\cos \alpha }{2} \ \rm[V] \)
\( \alpha = 0\)の時はダイオード整流の値となる
単相全波整流の平均電圧 \(V_d \ = \ 0.9V \times \displaystyle \frac{1+\cos \alpha }{2} \ \rm[V]\)
\( \alpha = 0\)の時はダイオード整流の値となる
練習問題
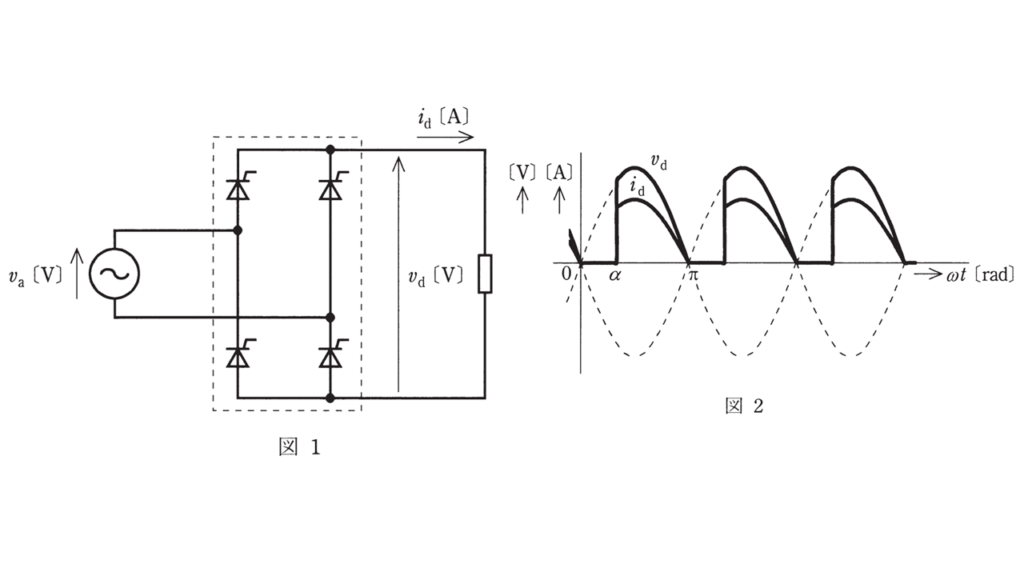
交流電圧\(v_a \ \rm[V]\)の実効値\(V_a\ \rm[V]\)が100Vで,抵抗負荷が接続された図1に示す半導体電力変換装置において,図2に示すようにラジアンで表した制御遅れ角\(\alpha \rm[rad]\)を変えて出力直流電圧\(v_a \ \rm [V]\)の平均値\(V_a \ \rm[V]\)を制御する。
度数で表した制御遅れ角\( \alpha \ \rm[°]\)に対する\(V_d\ \rm[V]\)の関係として,適切なものを次の\( \left(1 \right) \) ~ \( \left( 5 \right) \)のうちから一つ選べ。
ただし,サイリスタの電圧降下は,無視する。
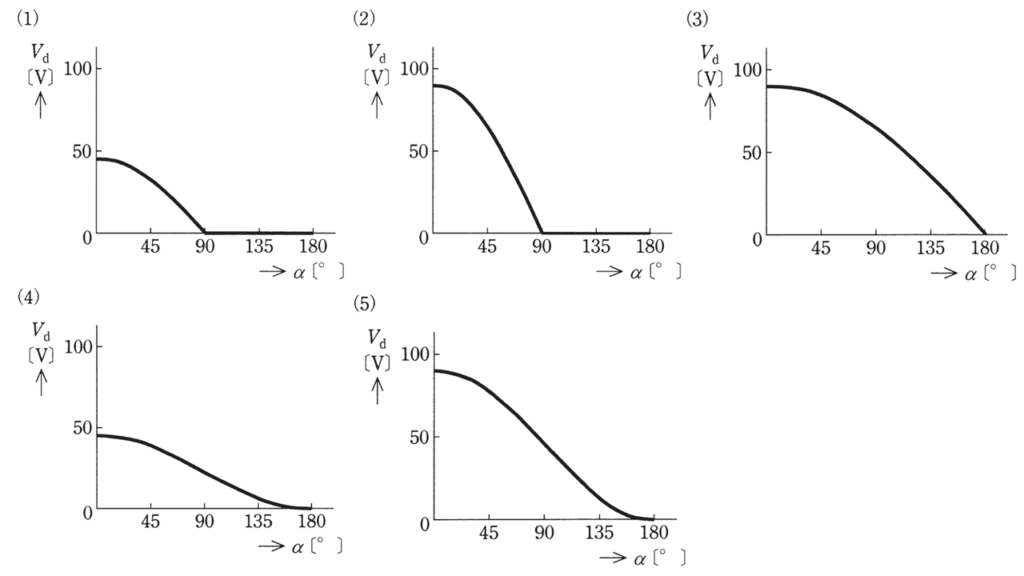
正解:(5)
問の文章より、電源電圧\(v_a\)の実効値が100Vであるから正弦波の式で表すと
\(v_a = 100\sqrt{2}\sin \omega t \)
となります。
実効値\(V \ \rm [V]\)の場合,全波整流回路の出力電圧の平均値は以下の公式で表されます。
\(V_d \ = \ 0.9V \times \displaystyle \frac{1+\cos \alpha }{2} \ \rm[V]\)
今回,実効値は100Vであるから\(V=100\)を代入すると
\( \begin{align} V_d \ &= \ 0.9\times 100 \times \frac{1+\cos \alpha }{2}\\ &=45 \times \left( 1+\cos \alpha \right) \ \rm[V] \tag{1} \end{align}\)
式(1)が得られます。
この式において制御角\( \alpha\)が\( 0°,45°,90°,135°,180°\)の時をそれぞれ計算すると以下の様になります。
\( \alpha = 0 °\)のとき
\(V_d = 45 \times \left( 1+\cos 0°\right) = 45 \times \left( 1+ 1 \right) = 90 \ \rm[V] \)
\( \alpha = 45°\)のとき
\(V_d = 45 \times \left( 1+\cos 45°\right) = 45 \times \left( 1+\displaystyle \frac{1}{\sqrt{2}} \right) = 76.8 \cdots \ \rm[V] \)
\( \alpha = 90 °\)のとき
\(V_d = 45 \times \left( 1+\cos 90°\right) = 45 \times \left( 1+ 0 \right) = 45 \ \rm[V] \)
\( \alpha = 135°\)のとき
\(V_d = 45 \times \left( 1+\cos 135°\right) = 45 \times \left( 1+\displaystyle \frac{-1}{\sqrt{2}} \right) = 13.1 \cdots \ \rm[V] \)
\( \alpha = 180°\)のとき
\(V_d = 45 \times \left( 1+\cos 180°\right) = 45 \times \left( 1+ (-1) \right) = 0 \ \rm[V] \)
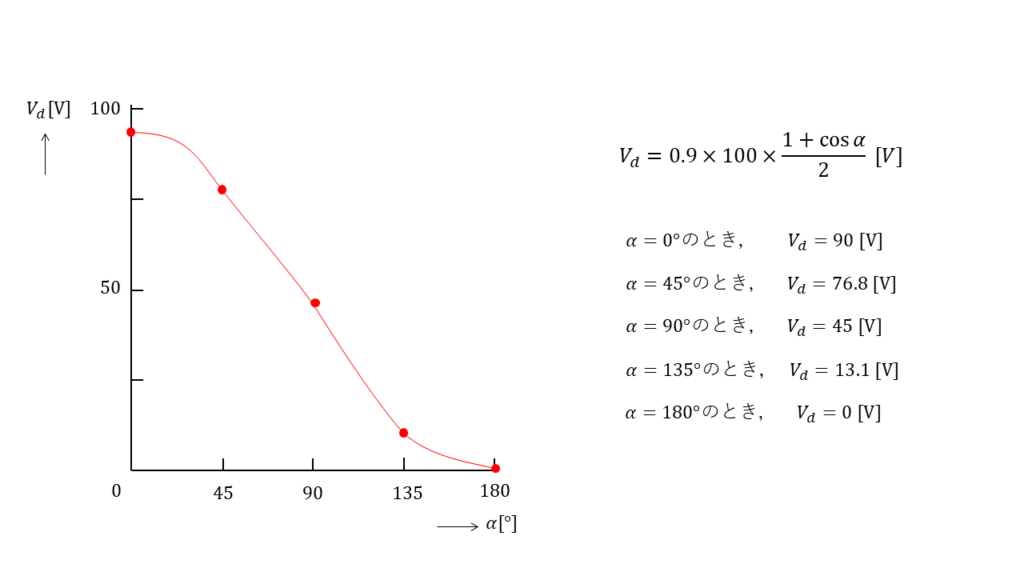
よって解答は(5)になります。
正解:(5)
問の文章より、電源電圧\(v_a\)の実効値が100Vであるから正弦波の式で表すと
\(v_a = 100\sqrt{2}\sin \omega t \)
となります。
実効値\(V \ \rm [V]\)の場合,全波整流回路の出力電圧の平均値は以下の公式で表されます。
\(V_d \ = \ 0.9V \times \displaystyle \frac{1+\cos \alpha }{2} \ \rm[V]\)
今回,実効値は100Vであるから\(V=100\)を代入すると
\( \begin{align} V_d \ &= \ 0.9\times 100 \times \frac{1+\cos \alpha }{2}\\ &=45 \times \left( 1+\cos \alpha \right) \ \rm[V] \tag{1} \end{align}\)
式(1)が得られます。
この式において制御角\( \alpha\)が\( 0°,45°,90°,135°,180°\)の時をそれぞれ計算すると
以下の様になります。
\( \alpha = 0 °\)のとき
\(V_d = 45 \times \left( 1+\cos 0°\right) = 45 \times \left( 1+ 1 \right) = 90 \ \rm[V] \)
\( \alpha = 45°\)のとき
\(V_d = 45 \times \left( 1+\cos 45°\right) = 45 \times \left( 1+\displaystyle \frac{1}{\sqrt{2}} \right) = 76.8 \cdots \ \rm[V] \)
\( \alpha = 90 °\)のとき
\(V_d = 45 \times \left( 1+\cos 90°\right) = 45 \times \left( 1+ 0 \right) = 45 \ \rm[V] \)
\( \alpha = 135°\)のとき
\(V_d = 45 \times \left( 1+\cos 135°\right) = 45 \times \left( 1+\displaystyle \frac{-1}{\sqrt{2}} \right) = 13.1 \cdots \ \rm[V] \)
\( \alpha = 180°\)のとき
\(V_d = 45 \times \left( 1+\cos 180°\right) = 45 \times \left( 1+ (-1) \right) = 0 \ \rm[V] \)

よって、正解は(5)になります。



コメント