- デルタ接続からスター接続へ変換したときの抵抗の大きさ
- デルタ⁻スター変換時の算出方法
- 三相交流回路でのデルタ⁻スター変化したときの電圧の変化
デルタ-スター変換
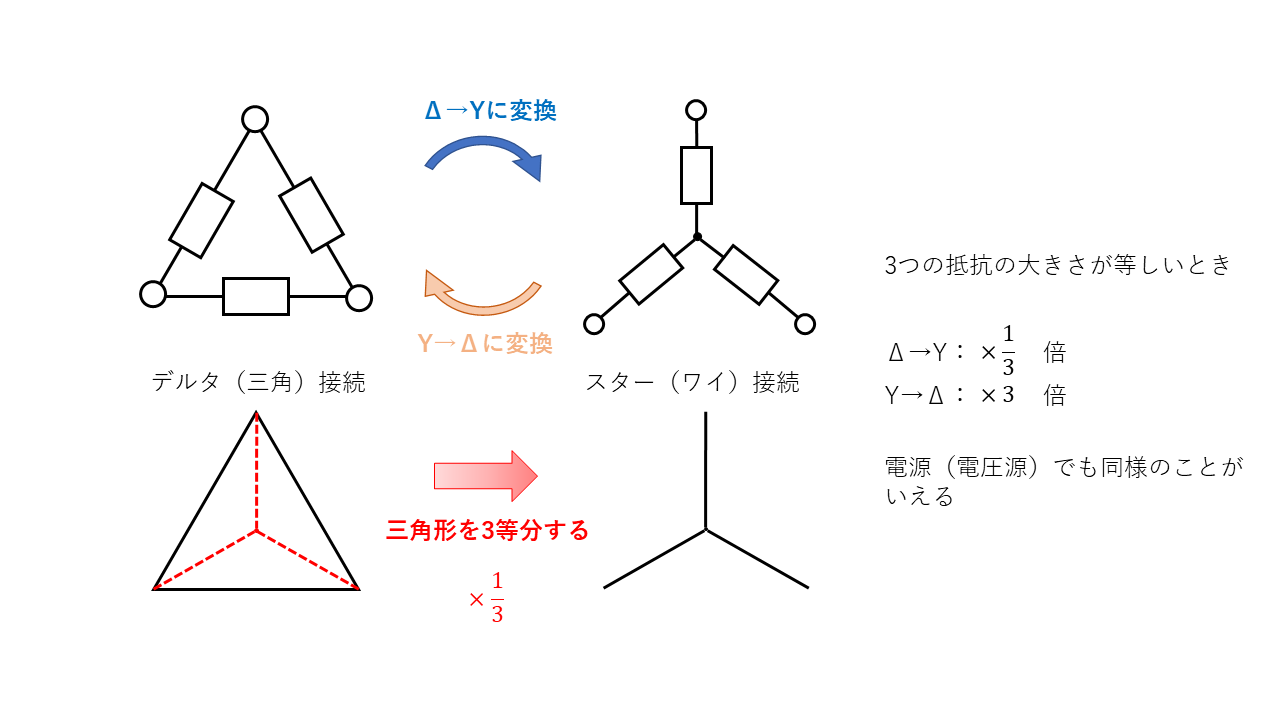
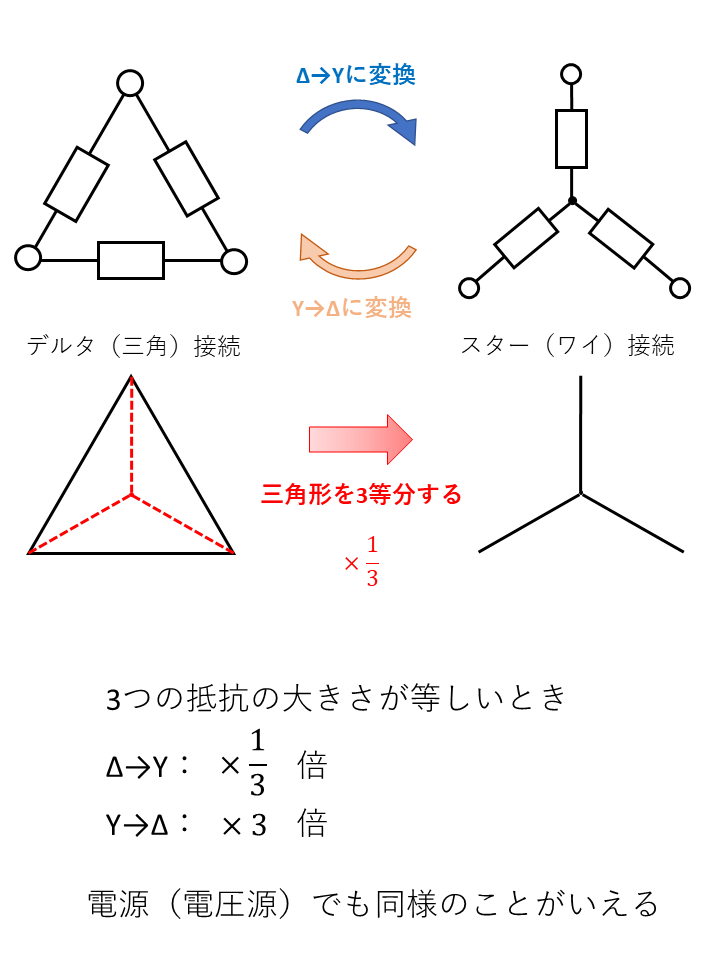

デルタ接続からスター接続に変換するとき、三等分にするように線を入れるので×\(\frac{1}{3}\)倍と覚えると分かりやすいと思います。
しかし、これは3つの抵抗の大きさが同じ場合にのみ用いることのできる考え方です。3つの抵抗の大きさがばらばらの時の変換方法について解説していきます。
デルタ接続からスター接続への変換方法
変換方法の手順

各端子間の抵抗の大きさが同じになれば変換完了!だから、各端子間の抵抗の式を書きだすところからスタートだよ。
- 各端子間の抵抗の大きさを表す式を書く
- 各端子間(例えば端子a-b間)の抵抗値が同じになるので、2つの式をイコールでつなぐ
- イコールでつないだ3つの式を連立して解く
Step1.デルタ接続、スター接続の各端子間の抵抗を表す式を書く
デルタ接続の場合
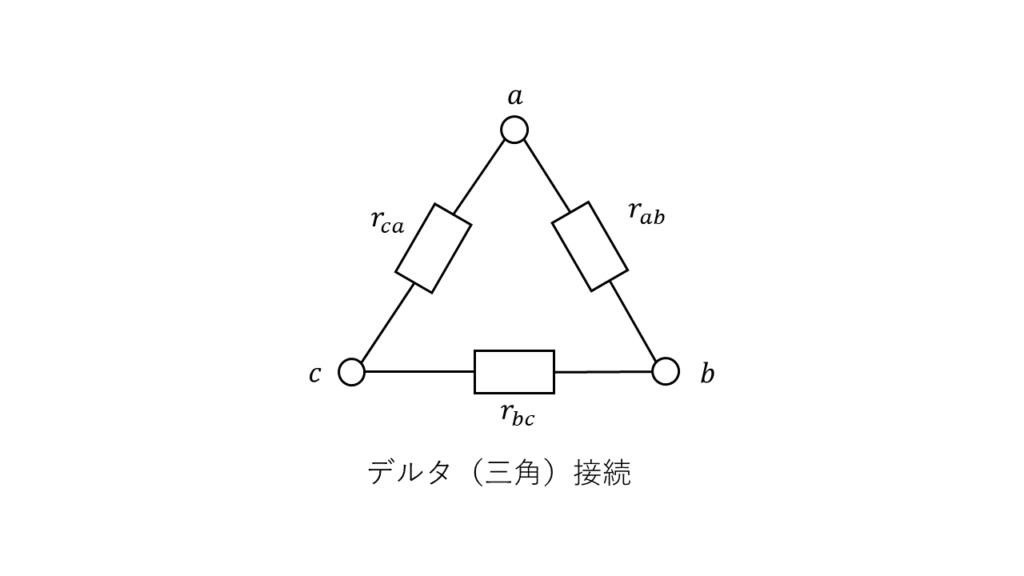
端子ab間
$$R{}_{ab}=\displaystyle\frac{r{}_{ab} \times\left(r{}_{bc}+r{}_{ca}\right)}{r{}_{ac}+r{}_{bc}+r{}_{ca}}$$
端子bc間、端子ca間も同様に計算することができるので、
$$R{}_{bc}=\displaystyle\frac{r{}_{bc} \times (r{}_{ab}+r{}_{ca})}{r{}_{ac}+r{}_{bc}+r{}_{ca}}$$
$$R{}_{ca}=\displaystyle\frac{r{}_{ca} \times (r{}_{ab}+r{}_{bc})}{r{}_{ac}+r{}_{bc}+r{}_{ca}}$$
スター接続の場合
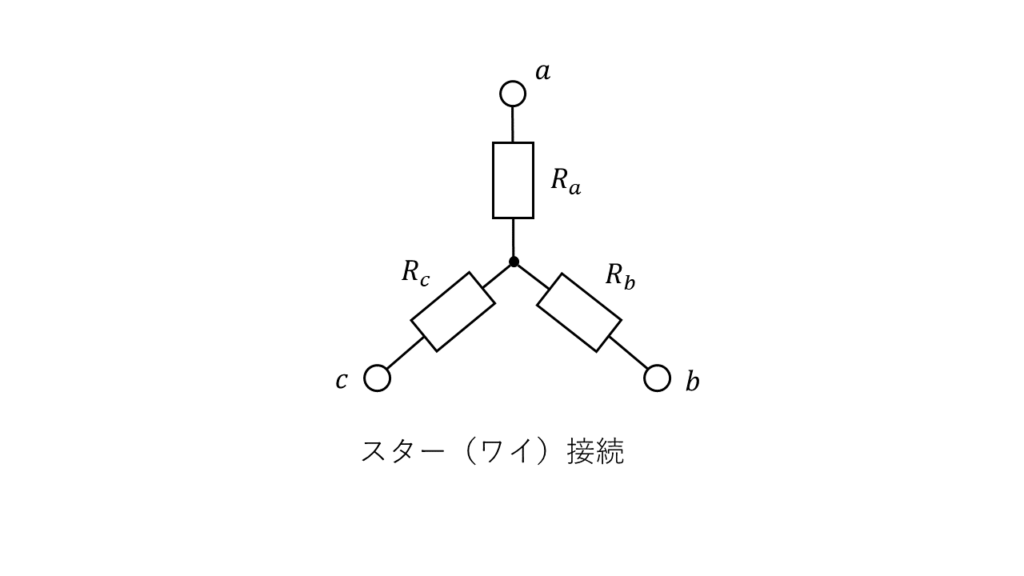
端子ab間の抵抗の大きさは、
$$R{}_{ab}=R{}_a +R{}_b$$
端子bc間、端子ca間も同様に計算することができるので、
$$R{}_{bc}=R{}_b +R{}_c$$
$$R{}_{ca}=R{}_c +R{}_a$$
Step2.デルタ接続、スター接続の端子間の抵抗は等しい式を書く
Step1で求めたそれぞれの式は、同じ端子間では等しくなることを利用して式を立てる。
$$R{}_{ab}=\displaystyle\frac{r{}_{ab} \times (r{}_{bc}+r{}_{ca})}{r{}_{ac}+r{}_{bc}+r{}_{ca}}=R{}_a +R{}_b$$
$$R{}_{bc}=\displaystyle\frac{r{}_{bc} \times (r{}_{ab}+r{}_{ca})}{r{}_{ac}+r{}_{bc}+r{}_{ca}}=R{}_b +R{}_c$$
$$R{}_{ca}=\displaystyle\frac{r{}_{ca} \times (r{}_{ab}+r{}_{bc})}{r{}_{ac}+r{}_{bc}+r{}_{ca}}=R{}_c +R{}_a$$
Step3.連立方程式を解く
Step2で書いた3つの式を使って抵抗の大きさを導く式を立てる。
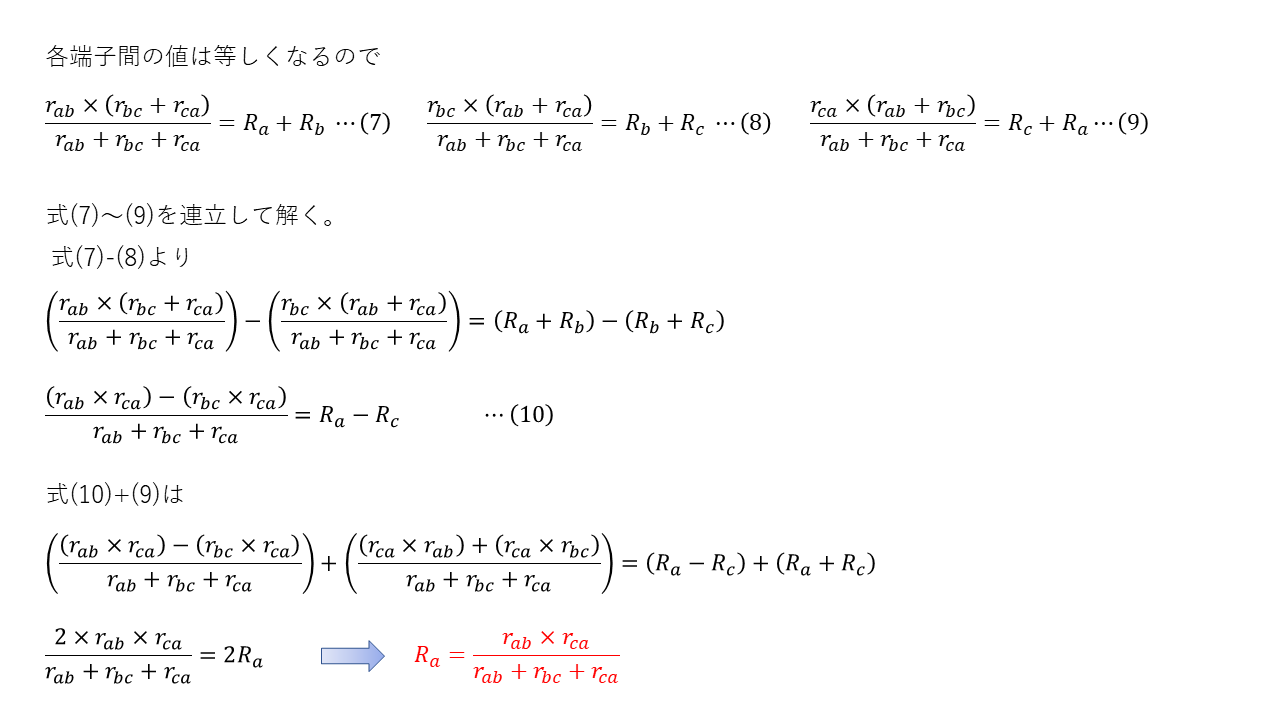

以上の3stepでデルタ⁻スター接続の変換ができます。電験2種ではインピーダンスの計算では必須といってもいいくらいの知識です。
試験で、導出から始める必要はありませんが知識として置いて損はないです。
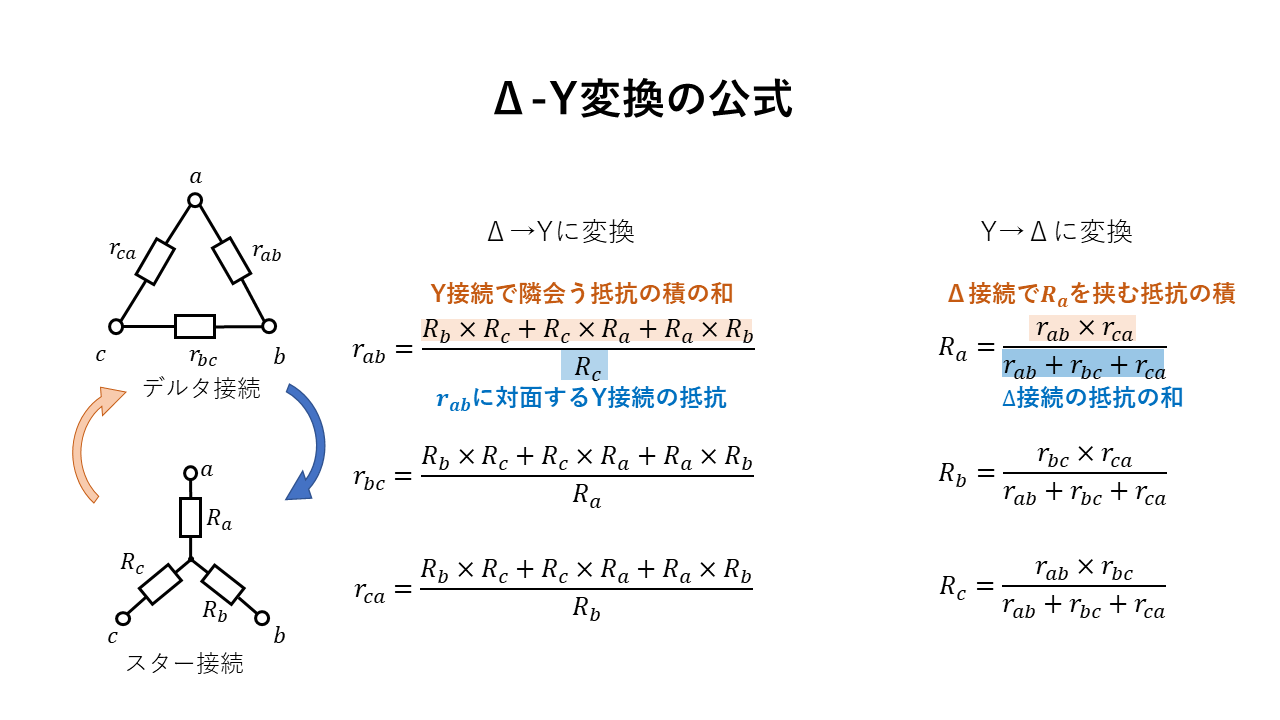
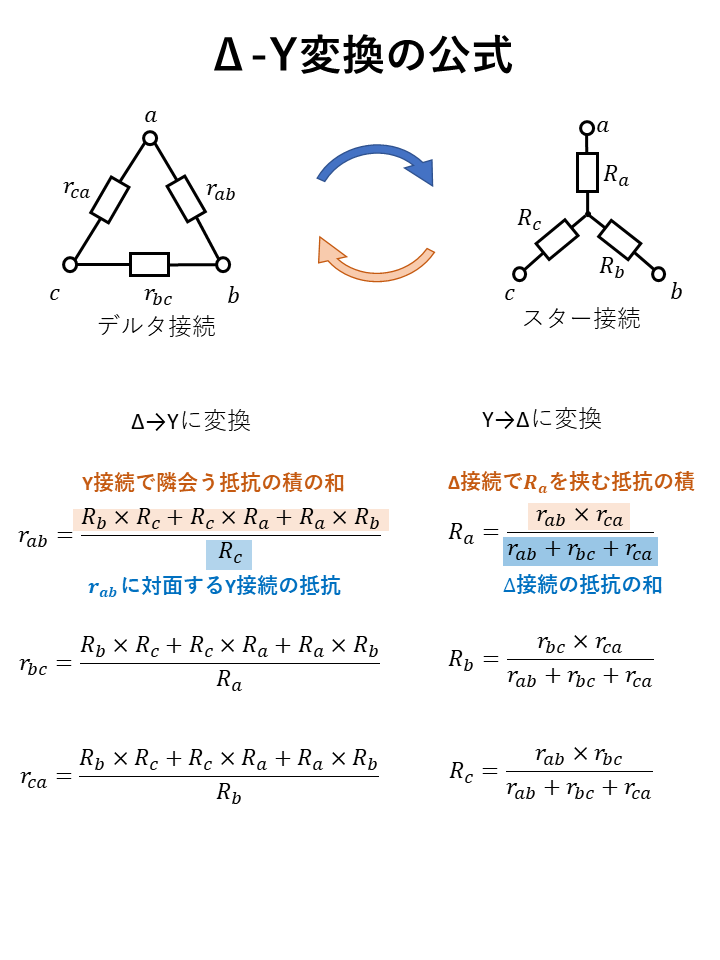
三相交流回路でのデルタ⁻スター変換
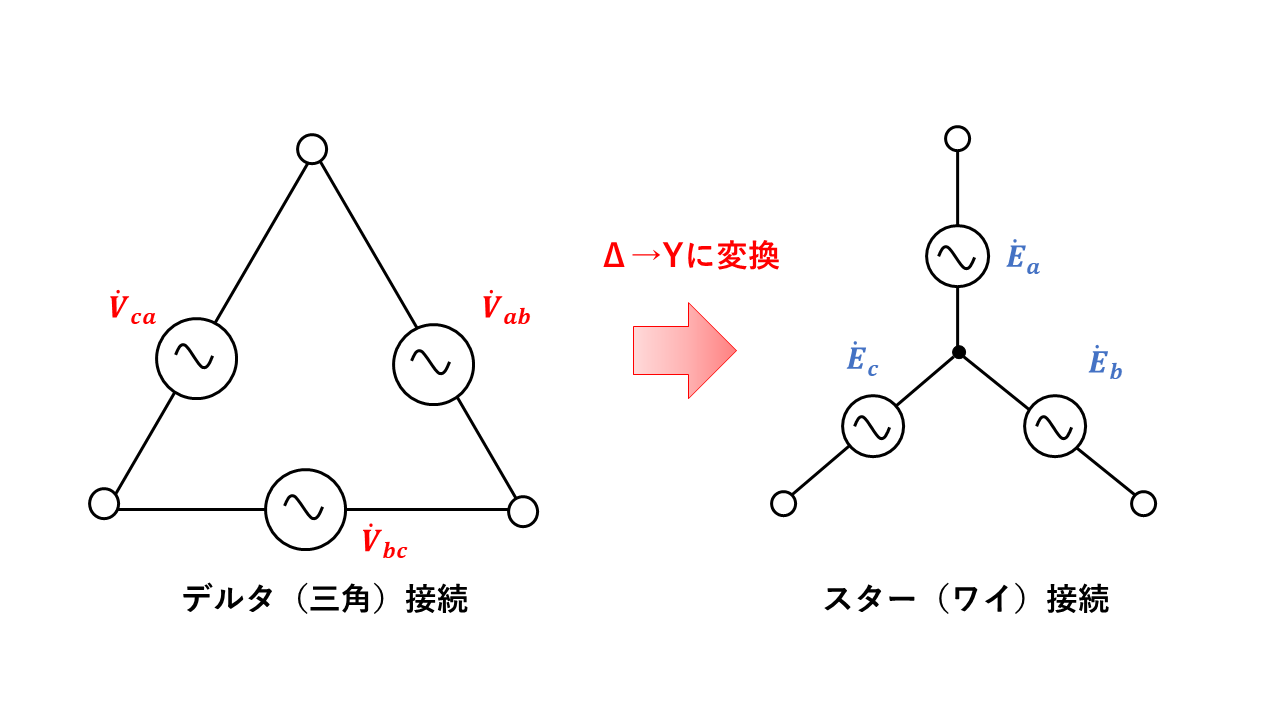
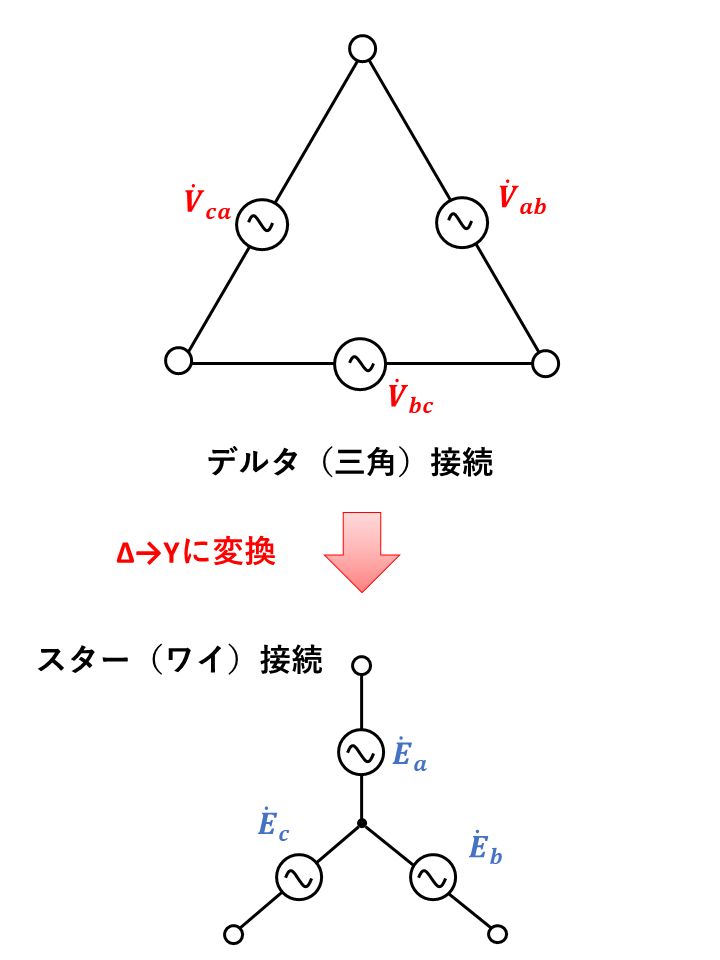
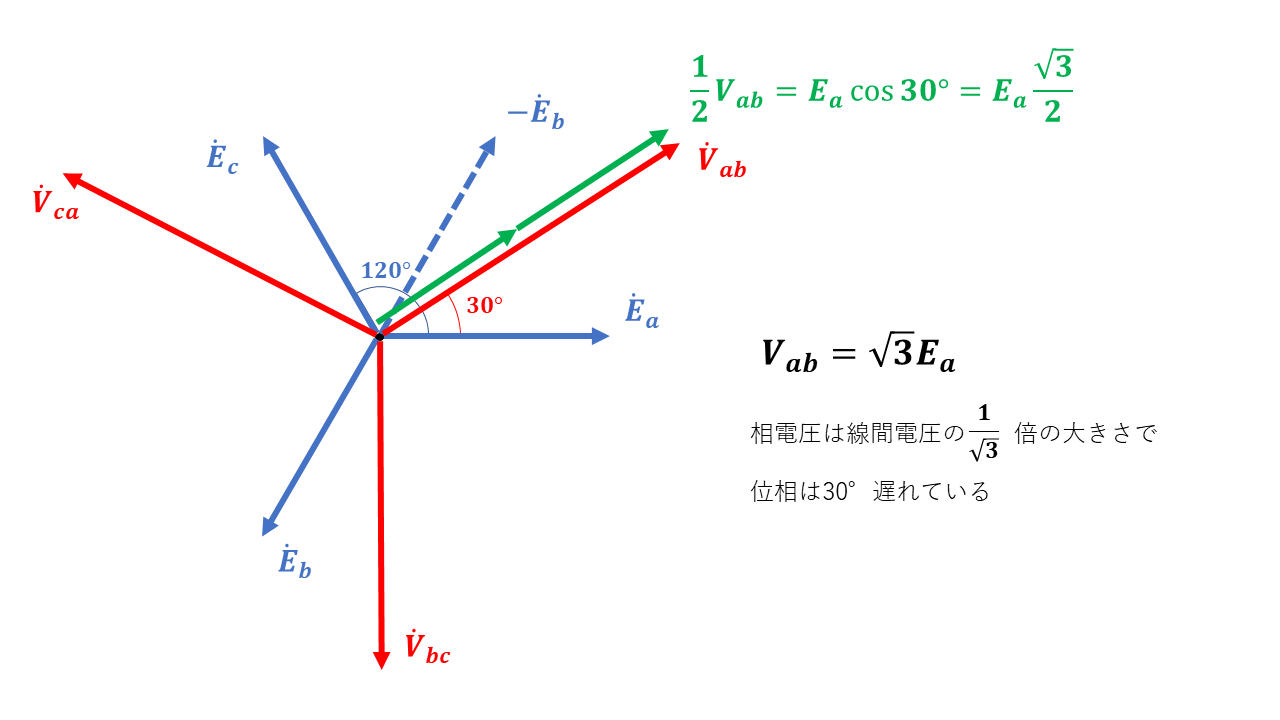
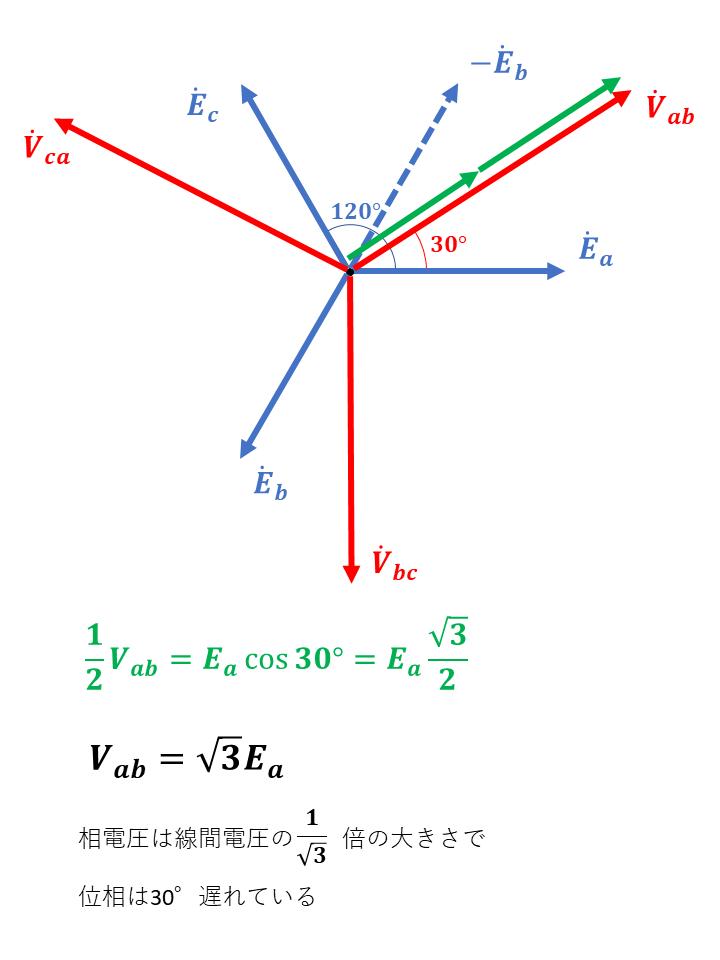
三相交流回路では、ベクトル図を書くことでイメージしやすくなります。
$$V{}_{ab}=\sqrt{3}E{}_{a}$$
線間電圧に比べ相電圧の大きさは\(\frac{1}{\sqrt{3}}\)倍となっている。
また、位相は線間電圧に比べ相電圧は30度遅れている。







コメント