電磁誘導とは?
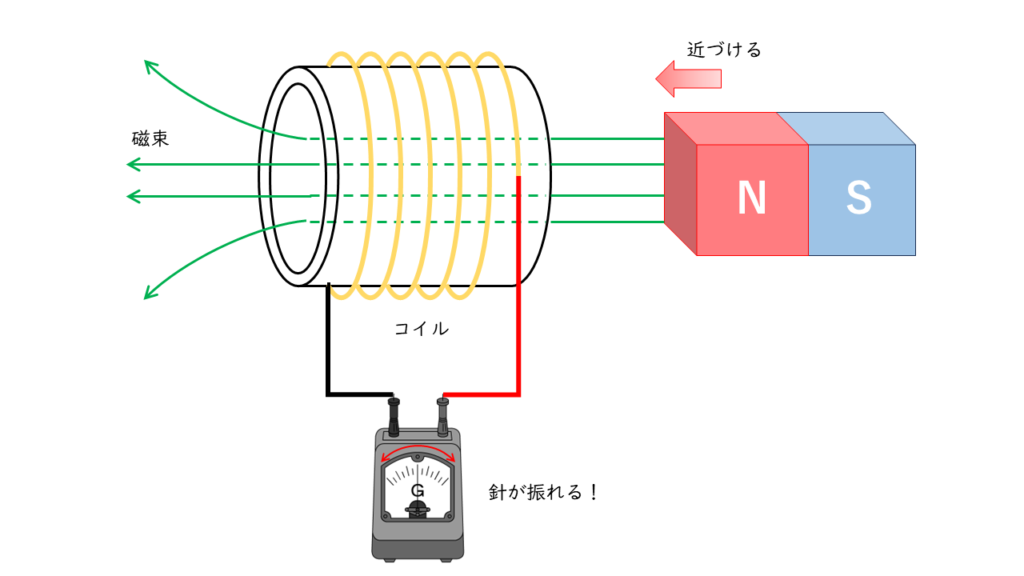
上図のようにコイルに磁石を近づけると,検流計(電流計)の針が動き電流が流れることが分かります。
これはコイルの内部の磁界が変化する際,コイルの磁界の変化を嫌う性質によって,磁界の変化に逆う向きに磁束を作るために起電力(電圧)が生じ,電流を流すためです。この現象を「電磁誘導」といい,この時に生じる電圧を「誘導起電力」,流れる電流を「誘導電流」といいます。
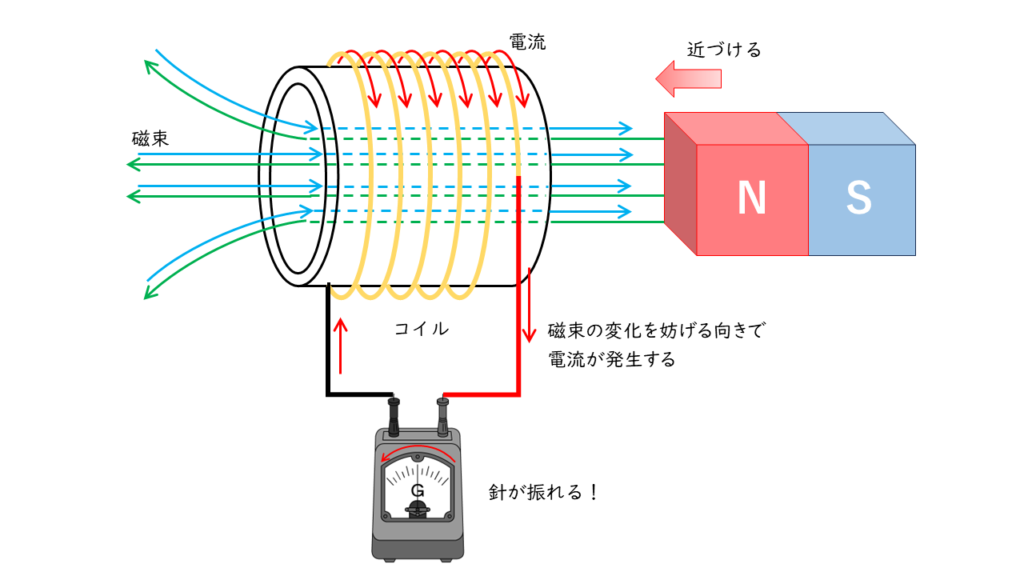
コイルに近づける磁石を速く動かすほど,電磁誘導による起電力は大きくなり,以下の式で表すことができます。
\(\begin{align} 誘導起電力 &=\ – \left( 巻数 \right) \times \displaystyle \frac{磁束の変化}{時間の変化} \\ \\ e &=\ – N \times \displaystyle \frac{\Delta \phi}{\Delta t} \end{align} \)
マイナスが付くのは磁界の変化に逆らう向きに起電力を発生させるためです。
電磁誘導に関連する法則
電磁誘導に関するファラデーの法則
誘導起電力 \(e\) の大きさは,コイル内部を貫く磁束 \(\phi\) の単位時間 \(\Delta t\) あたりの変化に比例することを表しています。
レンツの法則
誘導起電力の向きが,コイル内部の磁束の変化を妨げる向きに生じることを表しています。
磁束鎖交数とは?
コイルの内部を磁石の作る磁束が通り抜けることを「鎖交」と呼びます。これは,コイルと磁束が鎖が交わる様子に似ていることからついた呼び方です。
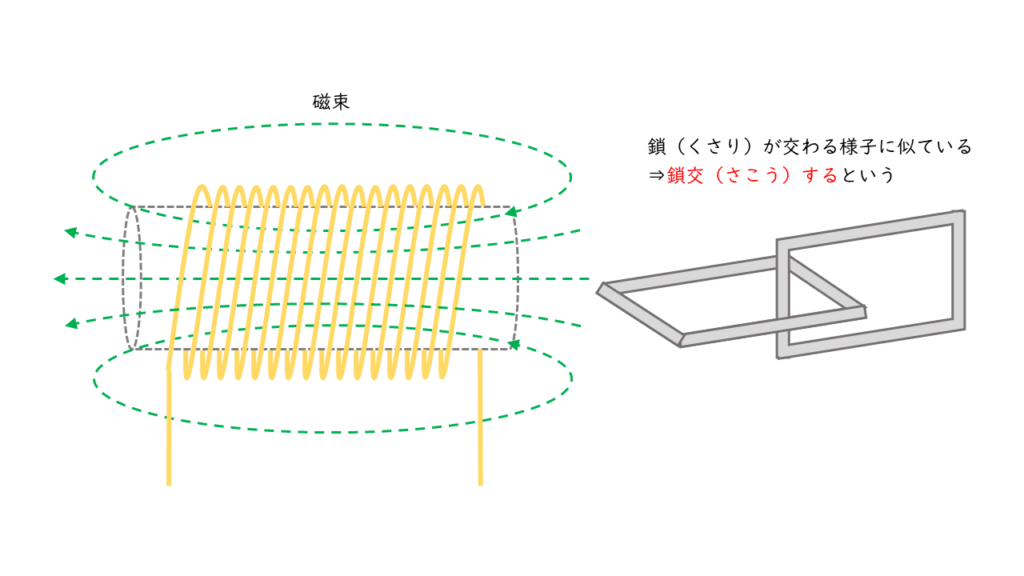
そのため,\(N\) 回巻きのコイルの内部を磁束 \(\phi \) が通り抜ける(鎖交する)数は,「磁束鎖交数」といいます。誘導起電力 \(e\) は,磁束鎖交数 \(N \phi\) が単位時間 \(\Delta t\) あたりにどれだけ変化するかを表した式と考えることもできます。
\( e = – \displaystyle \frac{\Delta N \phi}{\Delta t} = – N \displaystyle \frac{\Delta \phi}{\Delta t} \)
コイルが発生させる誘導起電力の向き
コイルが発生させる誘導起電力の向きは「フレミングの右手の法則」を用いて調べることができますが、学習を始めたばかりのうちは理解が難しいです。そこで、「右ねじの法則」を使って考える方法を解説します。
誘導起電力はコイルの内部を貫く磁束の変化を妨げる方向に発生するので,下図のように親指以外の指がコイルを貫く磁束とは反対を向くようにします。
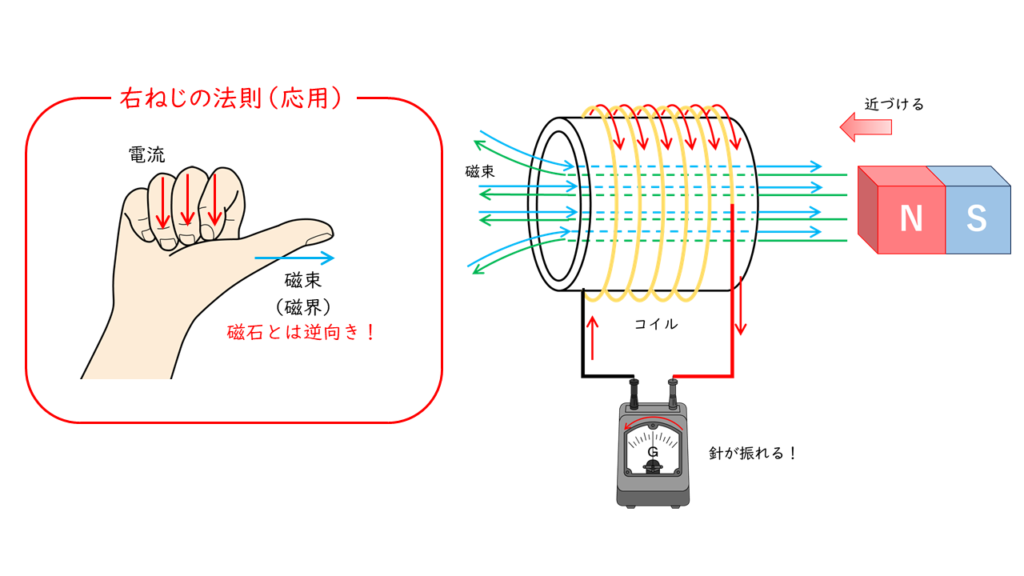
このようにすると,親指が誘導起電力の向き(誘導電流の向き)を表すことになります。
フレミングの右手の法則
誘導起電力が発生する向きは,「フレミングの右手の法則」によって調べることができます。
下図のように,親指,人差し指,中指を互いに直角にし,親指を導体の移動方向,人差し指を磁界(磁束)の方向に合わせると,中指は誘導起電力の方向を示すことになります。
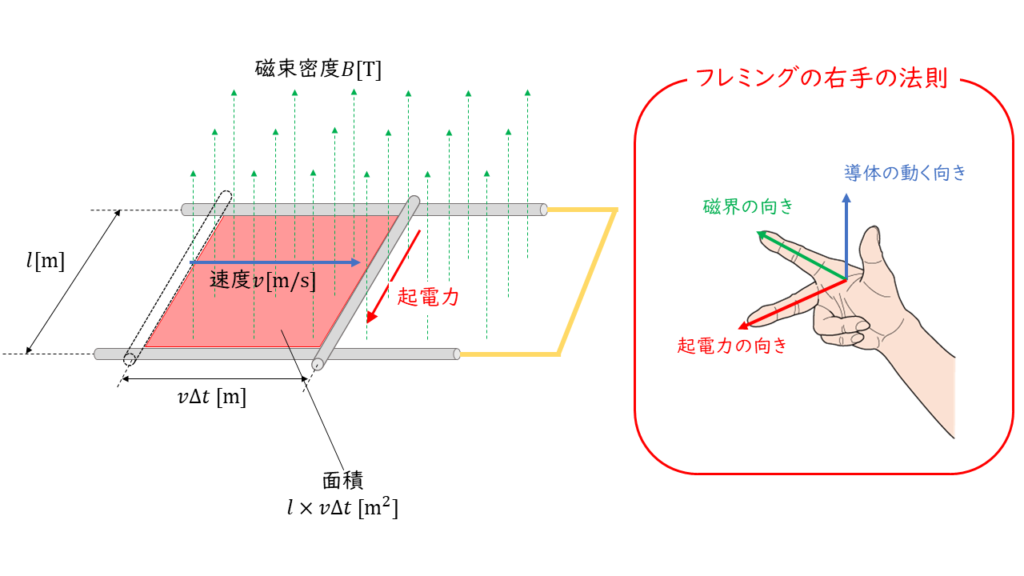
移動する導体による誘導起電力
下図のように磁束密度 \(B\ \rm T\) 中に置かれた,2本の平行な導体棒でできたレールの上を長さ \(l\ \rm m\) の導体を速度 \(v\ \rm m/s\) で移動させます。
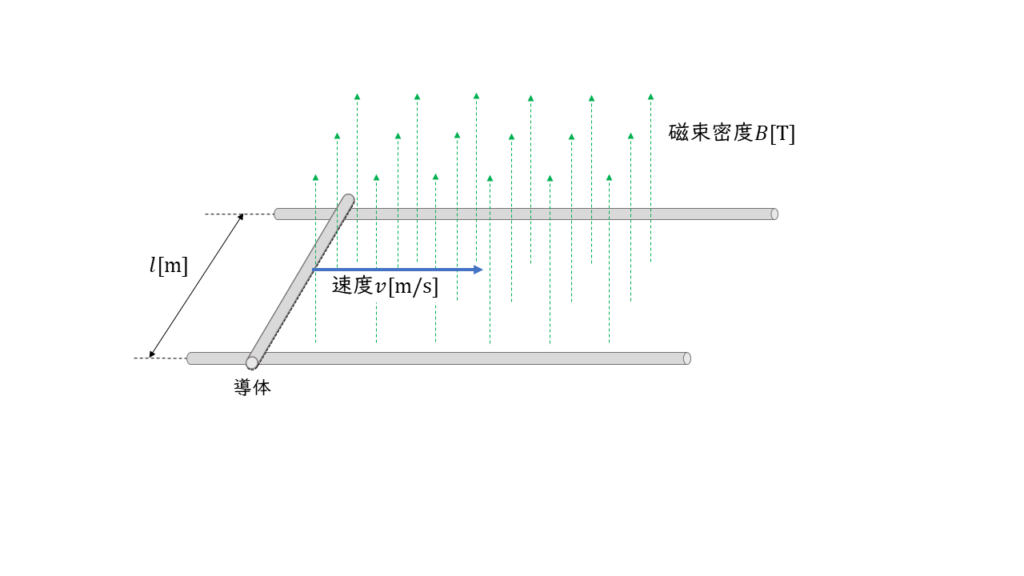
この時,レールの右端が接続されていれば,閉じた導体のループ(コイル)が形成されたとみなせるので,1回巻きのコイルに電磁誘導が発生します。
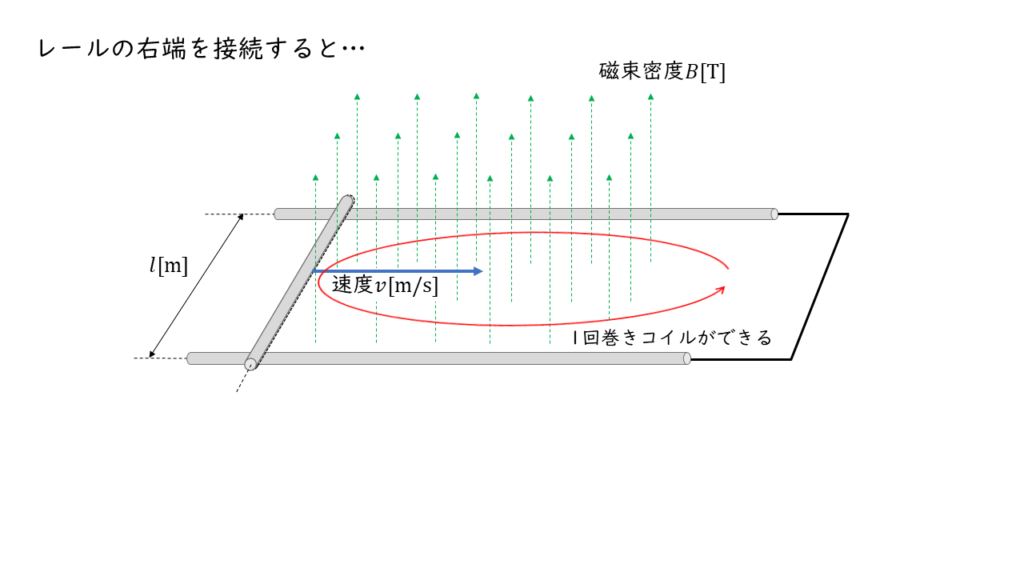
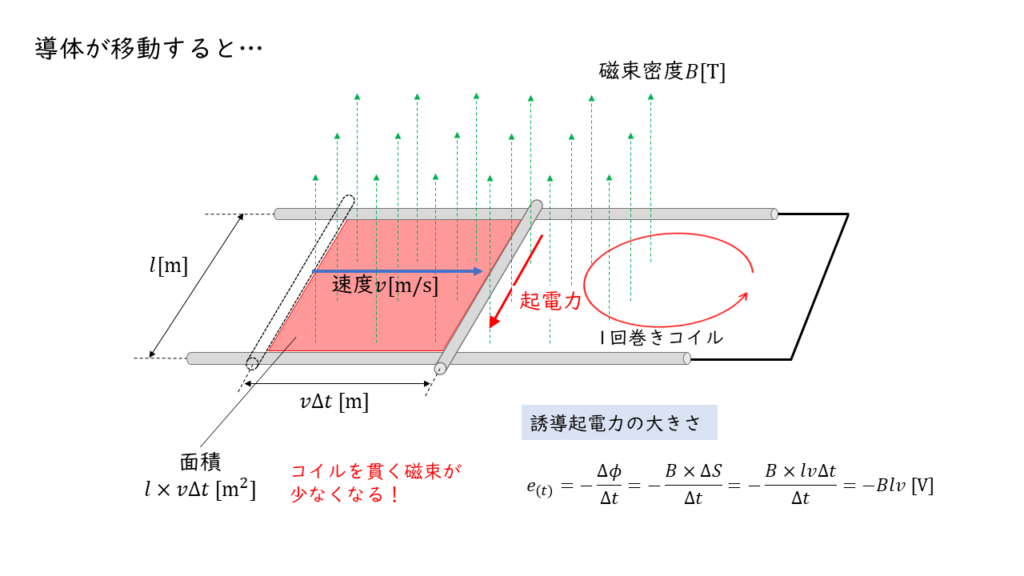
単位時間 \(\Delta t \ \rm s\) の間に導体は \(v \Delta t \ \rm m\) だけいどうするので,コイルを貫く磁束の変化 \(\Delta \phi\) は ,
\( \Delta \phi = B \times \left( v \Delta t \times l \right) \)
だけ,減少します。この時の誘導起電力 \(e\) の大きさは,
\(\begin{align} e &= – N \displaystyle \frac{\Delta \phi}{\Delta t} \ \ &= – 1 \times \displaystyle \frac{- B \times \left(v \Delta t l \right) }{\Delta t} \ \ &=Blv \end{align} \)
以上のように計算することができます。
下図のように導体と磁界(磁束)の作る角が直角でない場合は,磁界(磁束)に対して垂直な移動成分の速度を誘導起電力の式に当てはめます。
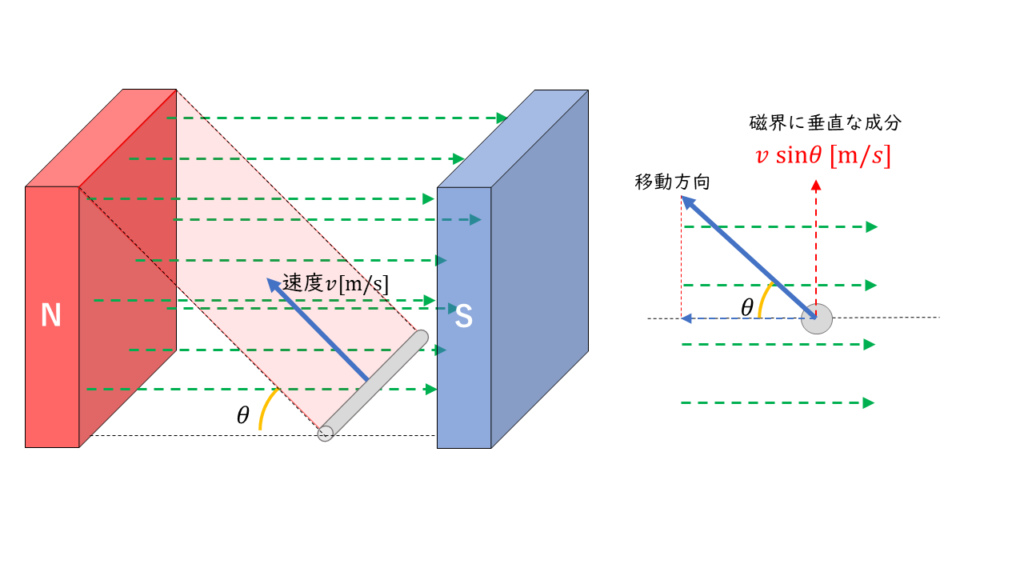
\( e = -Blv’ = -Blv \sin \theta \)








コメント