静電気の分野で学習したクーロンの法則と同じように,磁気においても磁気に関するクーロンの法則があります。
磁気に関するクーロンの法則
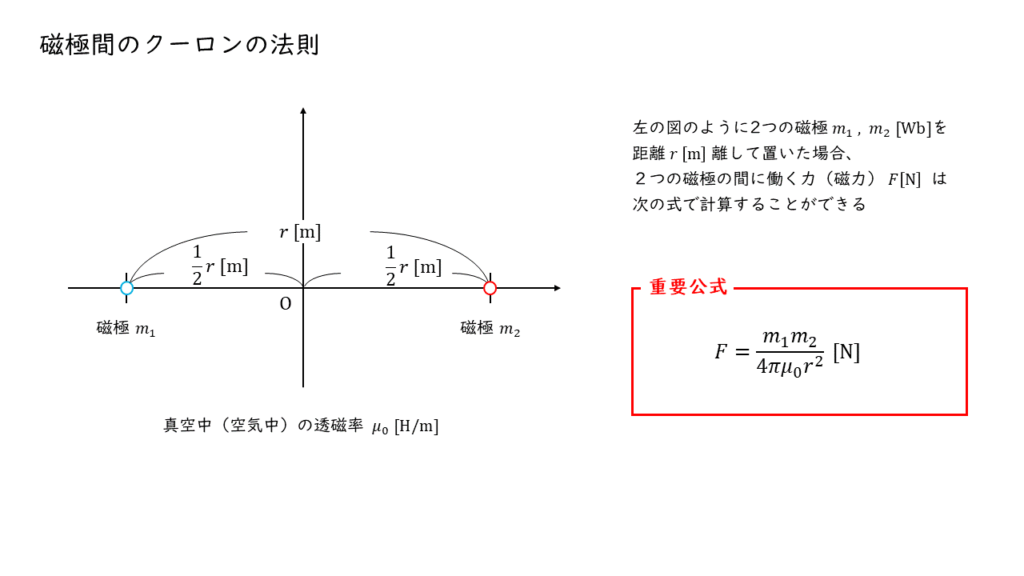
2つの点磁極が及ぼしあう磁力の大きさ \(F\ \rm[N]\) は,磁荷(磁極の強さ,記号:\(m\) ,単位:\(\rm [Wb] \) )を使って以下の式で表すことができます。
\( F = \displaystyle \frac{m_1 m_2}{4 \pi \mu_0 r^2} \)
磁荷:\(m_1 , m_2 \rm[Wb] \)
真空中の透磁率:\(mu_0 = 4\pi \times 10^{-7} \rm[H/m] \)
距離:\( r \rm[m]\)
上記の式から,2つの点磁極間に働く力の大きさは,2つの磁荷の積に比例し,2点間の距離に反比例することがわかります。
透磁率
透磁率とは,磁気(磁力線)の透しにくさを表すものです。真空中の透磁率( \(\mu_0\) )とは,何もない空間での磁気の透しにくさを表しています。
真空の透磁率 \(\mu_0 \ \rm[H/m]\) と,ある物質の透磁率 \(\mu \ \rm[H/m]\) の比率のことを比透磁率 \(\mu_r\) といいます。
\( \mu = \mu_0 \times \mu_r \ \rm[H/m] \)
磁力の向き
力のことを考えるうえで忘れてはいけないのは,力の働く向きです。
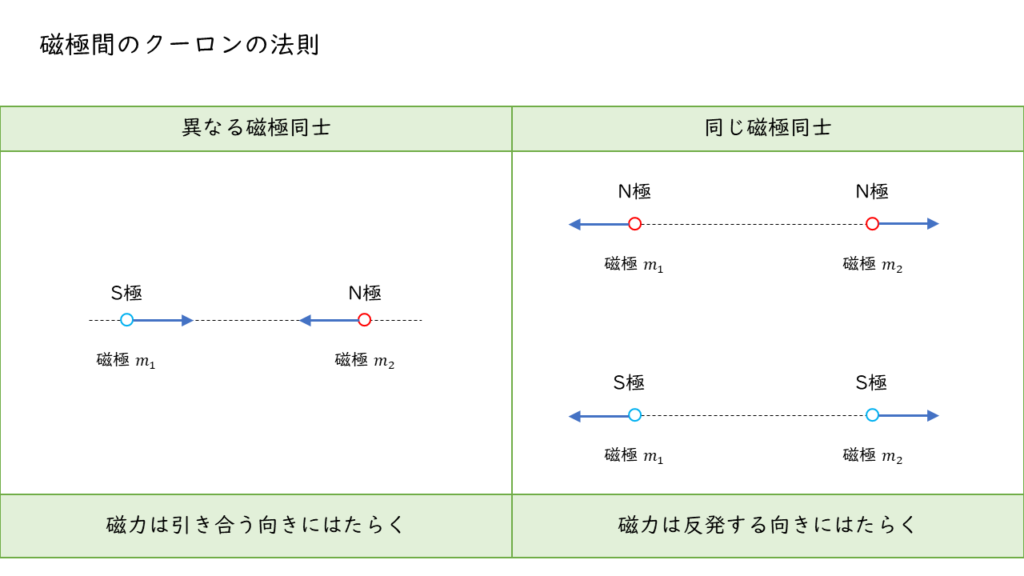
磁力の向きは,2つの点磁極を結ぶ一直線上に働き,磁気に関するクーロンの法則によって2つの点磁極(磁荷)に働く力の向きは,同種の磁極同士なら反発し,異種の磁極同士なら引き合う力が働きます。
3つの点磁極間にはたらく磁力の計算
実際の試験問題では,静電気のクーロンの法則と同様に3つの点磁極がおかれた場合の,磁力を計算させるパターンで出題されることが多いです。
例題 理論科目 平成30年度 問3
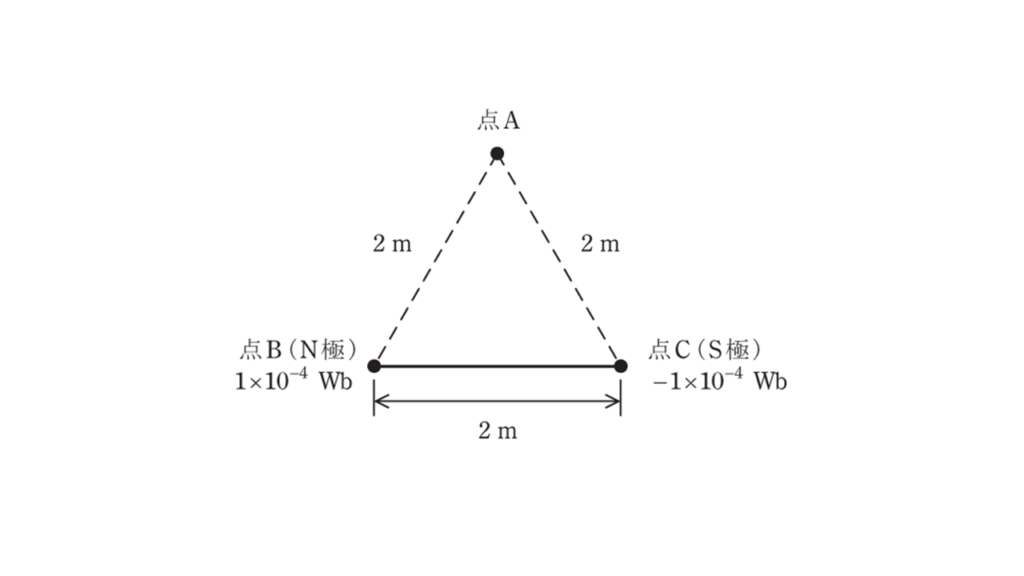
長さ \(2\ \rm m\) の直線状の棒磁石があり,その両端の磁極は点磁荷とみなすことができ,その強さは,N極が \(1×10^{-4}\ \rm Wb\) ,S極が \(-1×10^{-4}\ \rm Wb\) である。図のように,この棒磁石を点 \(BC\) 間に置いた。このとき,点 \(A\) の磁界の大きさの値 \(\rm [A/m]\) として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,点 \(A\) ,\(B\) ,\(C\) は,一辺を \(2\ \rm m\) とする正三角形の各頂点に位置し,真空中にあるものとする。真空の透磁率は \(μ_0 = 4 \pi×10^{-7} \ \rm H/m\) とする。また,N極,S極の各点磁荷以外の部分から点 \(A\) への影響はないものとする。