- 電源が複数ある回路の計算方法が分かる
- 重ね合わせの理の解法手順
複数の電源を持つ回路の計算方法
複数の電源を持つ回路の計算方法には次の2つがあります。
- 重ね合わせの理
- キルヒホッフの法則
2つの解法のメリット、デメリットは以下の通りです。
重ね合わせの理
- 回路が簡単
- 計算が簡単
- 計算量が多くなる
- 複雑な回路の計算には時間がかかる
キルヒホッフの法則
- 複雑な回路にも応用できる
- 1つ1つの計算式は簡単
- 式を立てるのがやや難しい
- 方程式を解く必要がある
どちらにもメリット、デメリットはありますが計算が不得意な方は、”重ね合わせの理”がおすすめです。

計算が苦手だから、まずは重ね合わせの理から勉強してみよう!
重ね合わせの理の解法
電圧源は短絡して1つの電源回路に分ける
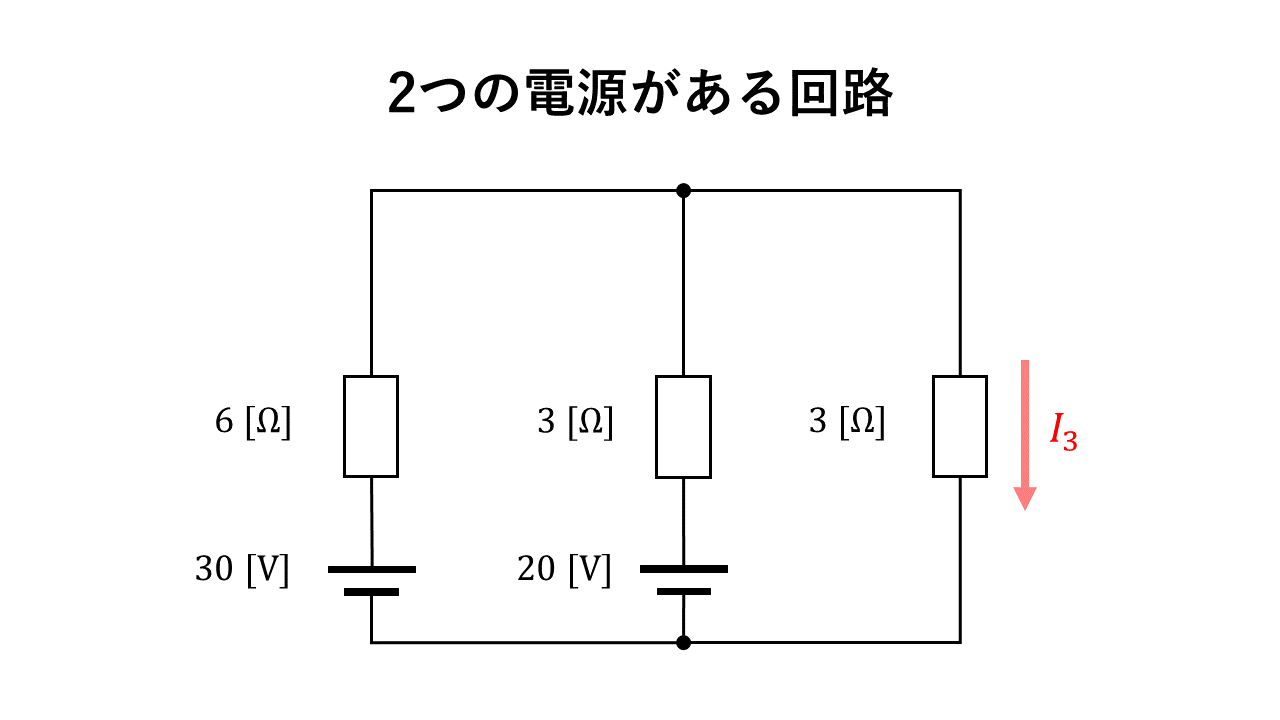
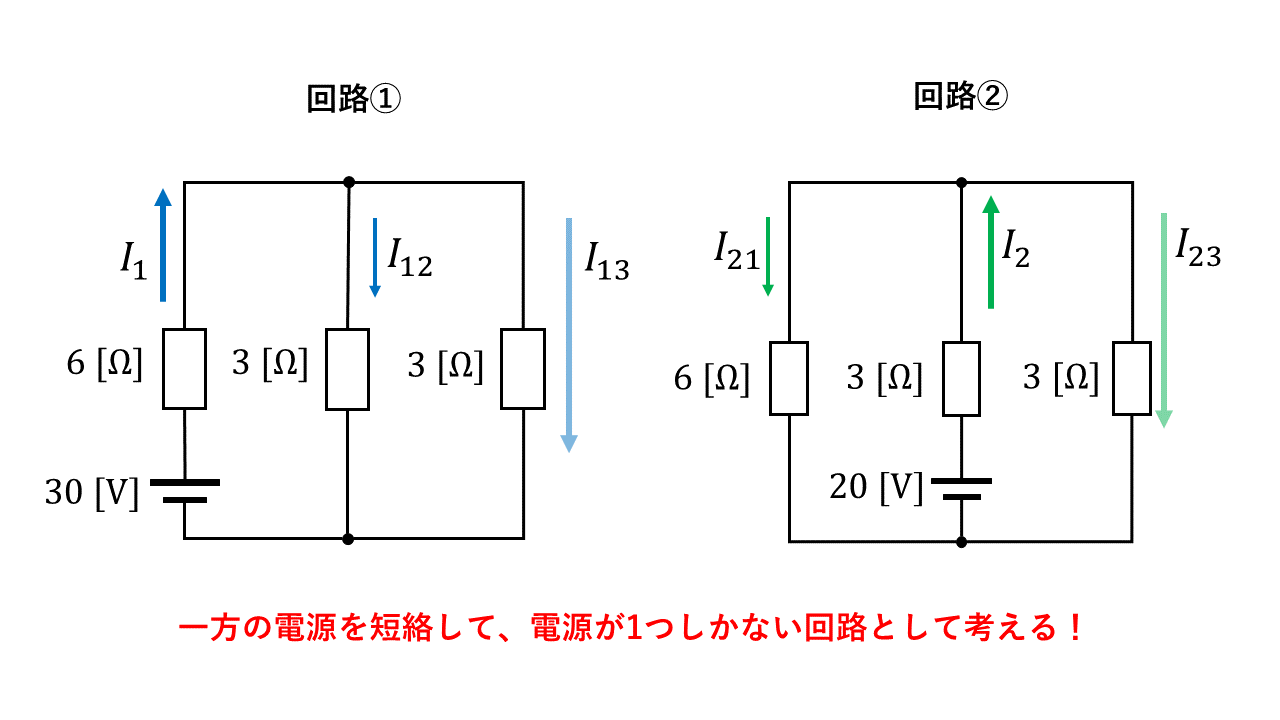
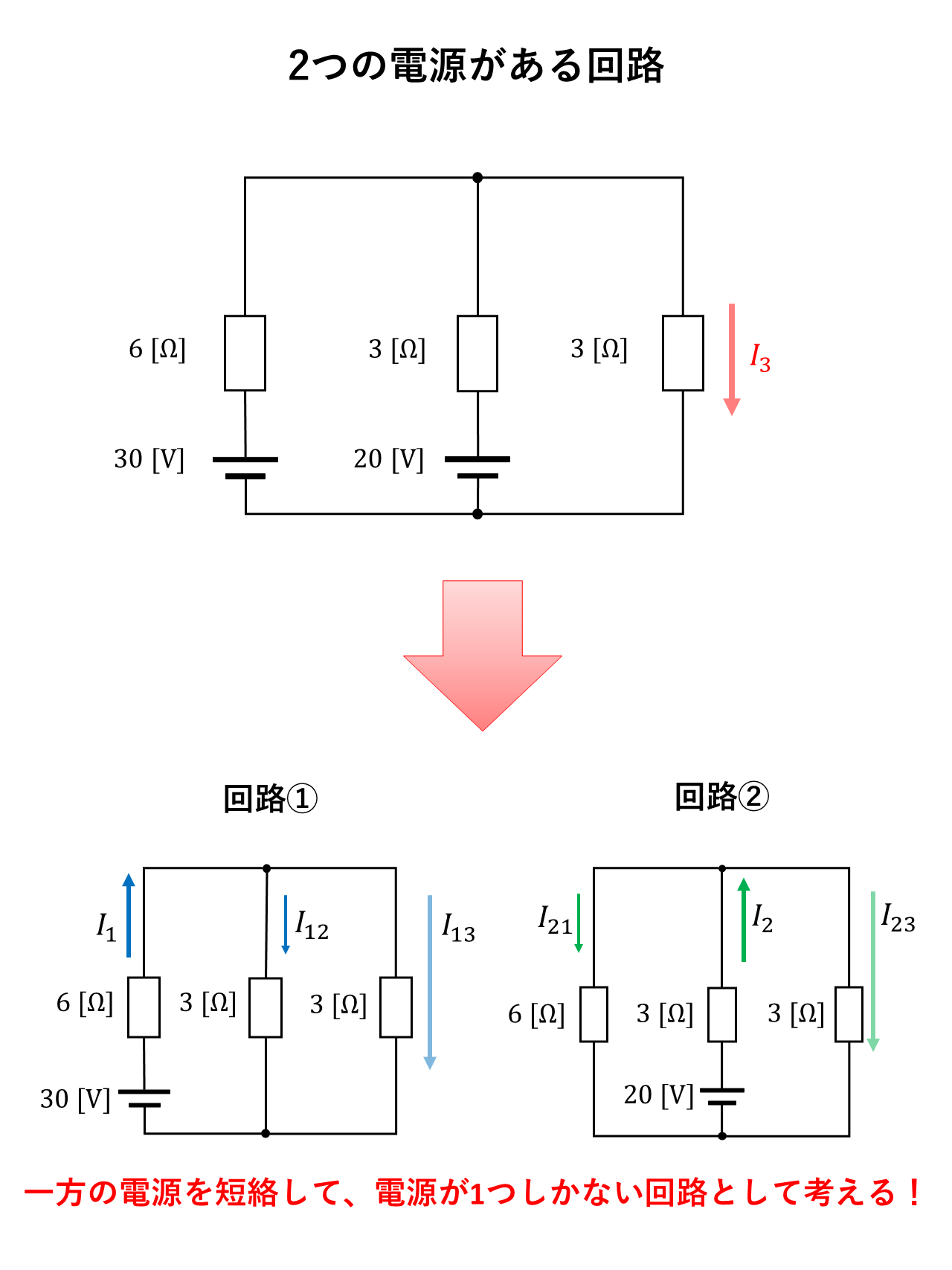
各回路の電流を計算する
回路①
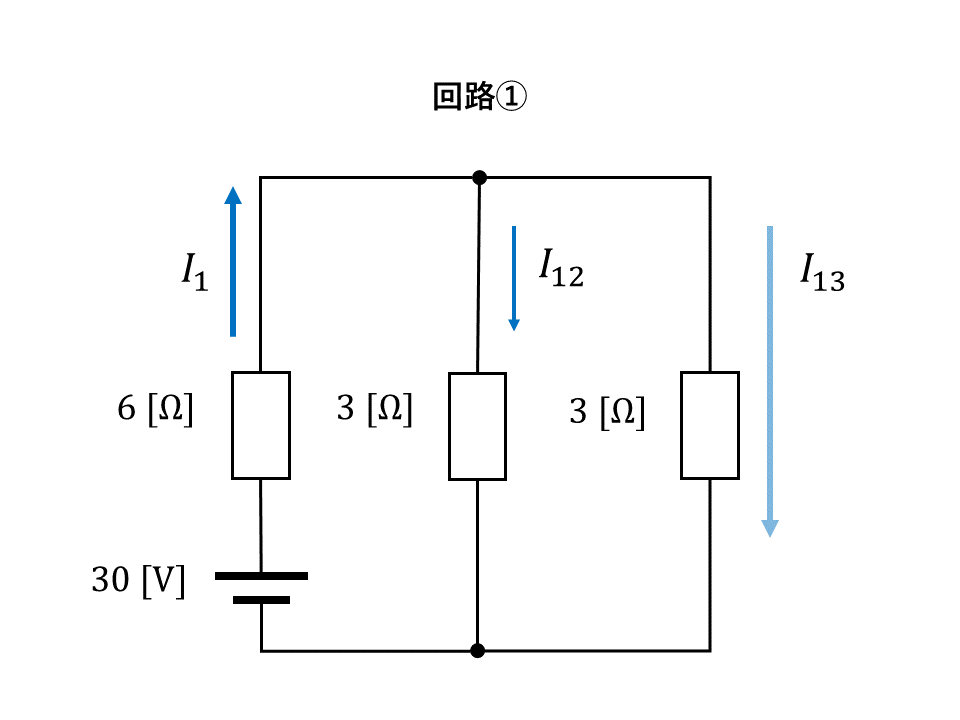
右端の3[Ω]の抵抗に流れる電流\(I{}_{13}\)を求める。
回路全体の抵抗を求める
$$R=\displaystyle\frac{1}{\displaystyle\frac{1}{3}+\displaystyle\frac{1}{3}}+6$$
$$=\displaystyle\frac{1}{\displaystyle\frac{2}{3}}+6$$
$$=\displaystyle\frac{3}{2}+6$$
$$=1.5+6=7.5$$
電流\(I{}_{13}\)の大きさを求める
電流\(I{}_1\)を求める
$$I{}_1 = \frac{30}{7.5}=4[A]$$
電流\(I{}_{13}\)の大きさは
$$I{}_{13}=4\times \displaystyle\frac{1}{\displaystyle\frac{1}{3}+\displaystyle\frac{1}{3}} \times \frac{1}{3}=2.0[A]$$
回路②
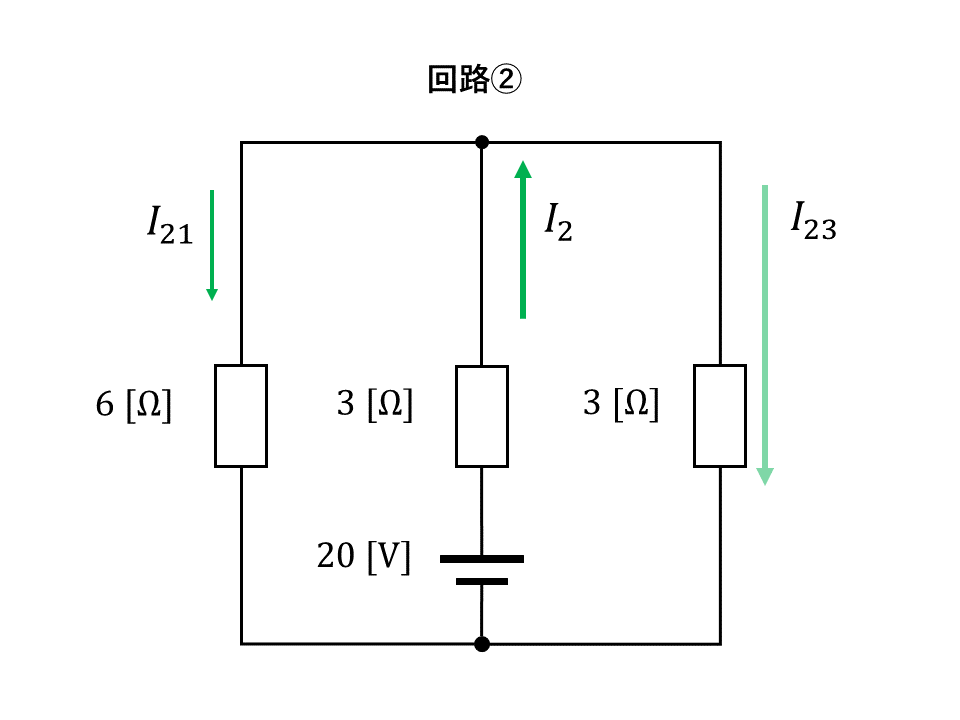
右端の3[Ω]の抵抗に流れる電流\(I{}_{23}\)を求める。
回路全体の抵抗を求める
$$R=\displaystyle\frac{1}{\displaystyle\frac{1}{3}+\displaystyle\frac{1}{6}}+3$$
$$=\displaystyle\frac{1}{\displaystyle\frac{2}{6}+\displaystyle\frac{1}{6}}+3$$
$$=\displaystyle\frac{1}{\displaystyle\frac{3}{6}}+3$$
$$=\frac{6}{3}+3$$
$$=2+3=5$$
電流\(I{}_{23}\)の大きさを求める
電流\(I{}_2\)を求める
$$I{}_2 = \frac{20}{5}=4[A]$$
電流\(I{}_{23}\)の大きさは
$$I{}_{23}=4\times \displaystyle\frac{1}{\displaystyle\frac{1}{3}+\displaystyle\frac{1}{6}} \times \displaystyle\frac{1}{3}=2.666[A]$$
分割して計算した電流を足し合わせる
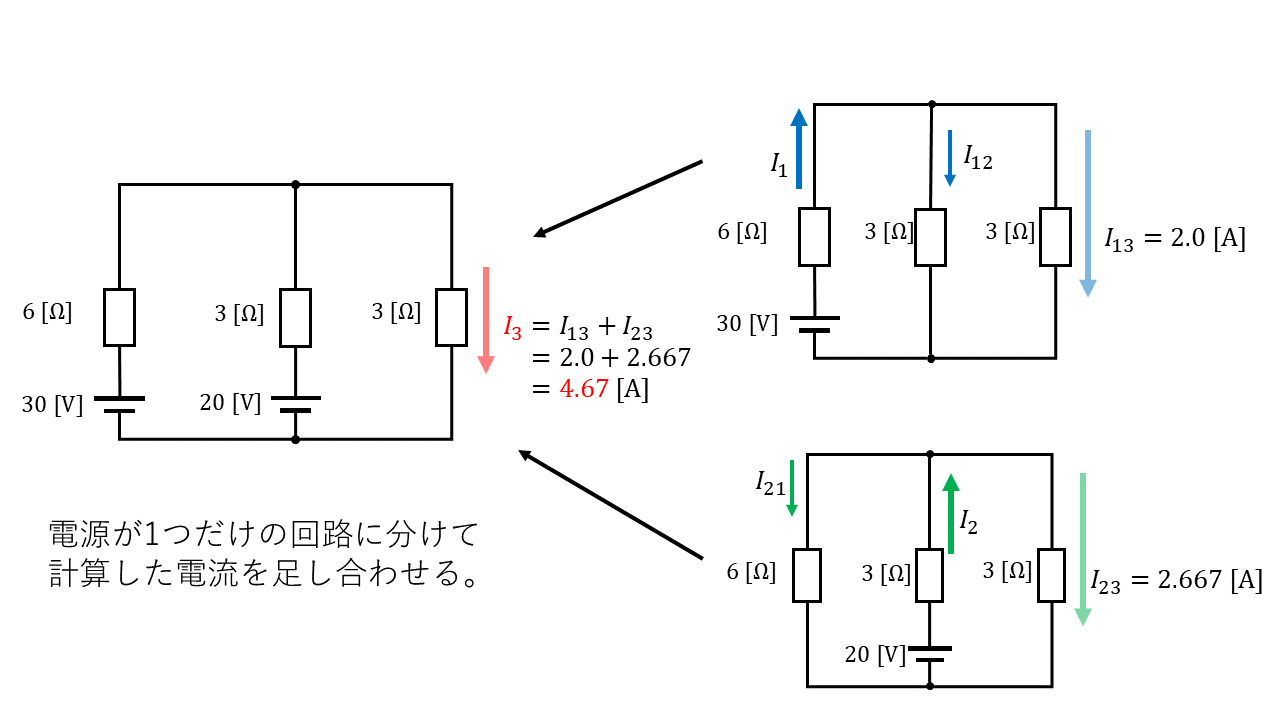
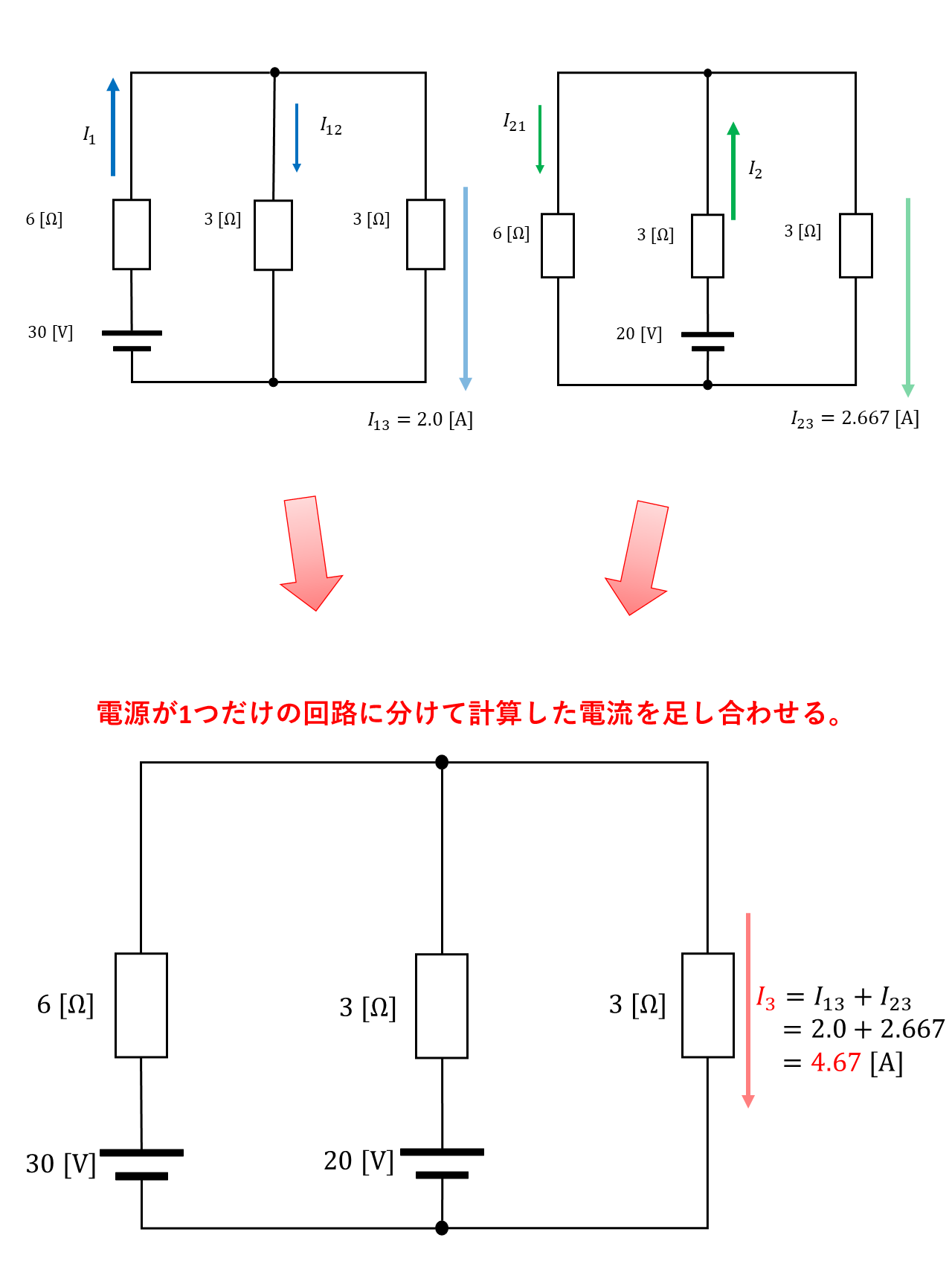

電源の数が増えると計算量が増えるけど、シンプルな式の計算なので式を立てるのが苦手な方は”重ね合わせの理”で解き進めるのがおすすめです!






コメント