同期発電機の特性に関する問題は、かなり高頻度で出題されています。中でも「同期インピーダンスと短絡比」に関する問題は特に出題数が多いです。
等価回路から、同期インピーダンスが土嚢用に導出されるのか、短絡比と同期んぴーダンスにはどのような関係性があるのかを理解することで計算問題での間違いは少なくなります。
今回は、三相同期発電機の特性について解説していきます。
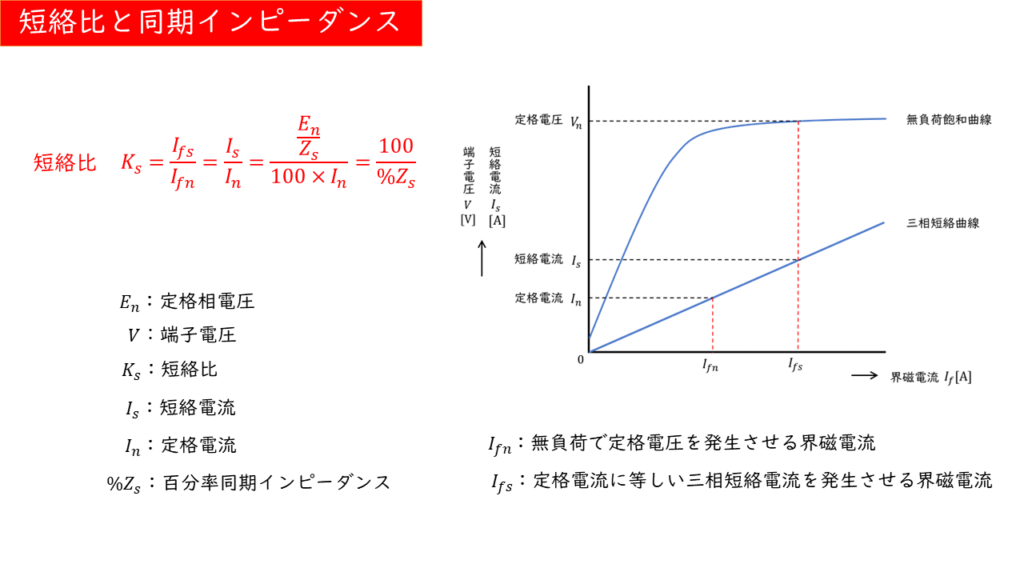
無負荷飽和曲線
三相同期発電機を無負荷のまま、定格速度で運転している場合における、端子電圧\(V\) [V]と界磁電流\(I_f\)[A]の関係性を示した曲線を「無負荷飽和曲線」といいます。
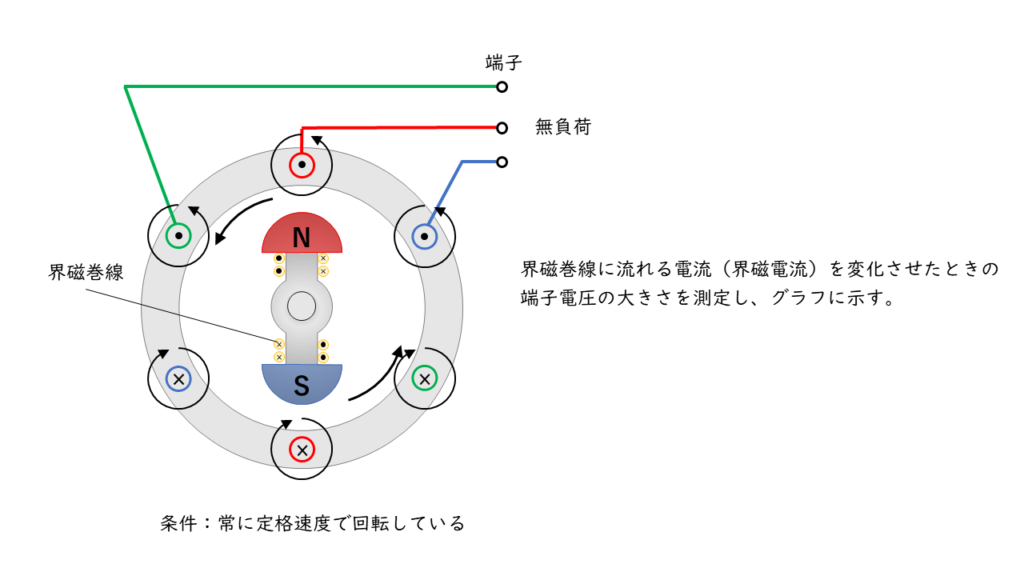
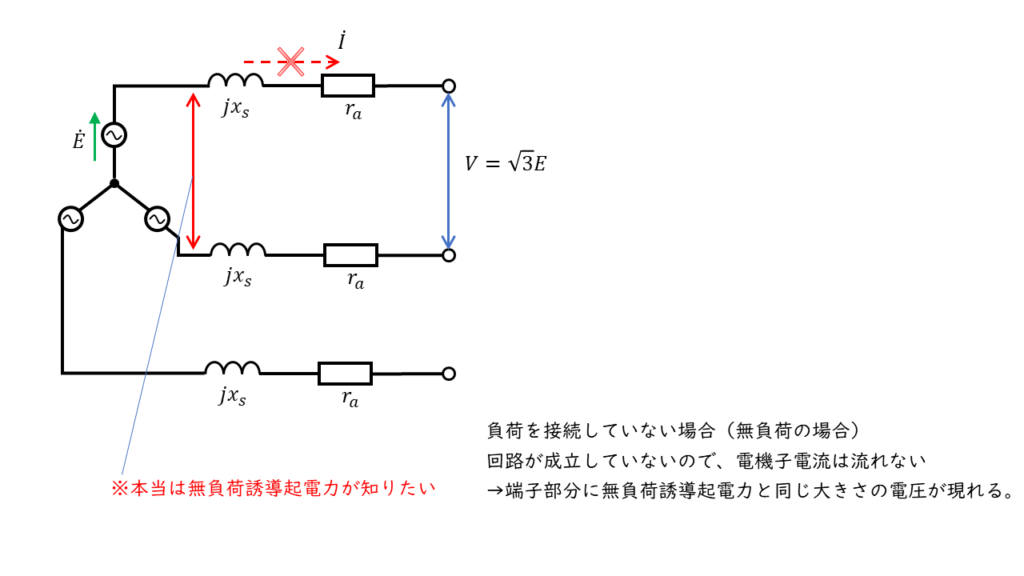
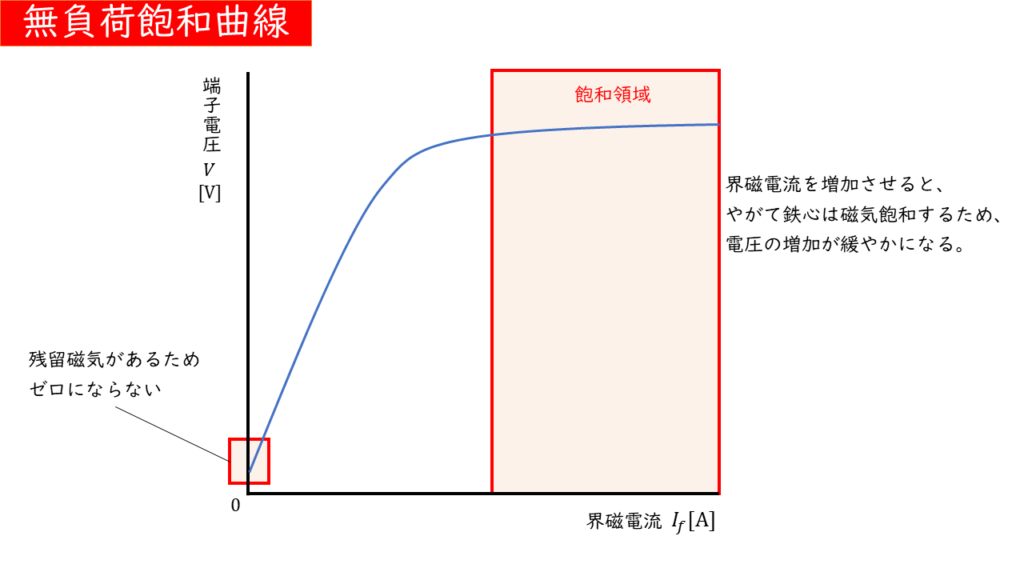
界磁電流が小さい領域では、端子電圧と界磁電流はほぼ比例の関係にあります。
界磁電流を増加させていくと、鉄心が磁気飽和を起こすため、端子電圧の増加が緩やかになり、ほとんど変化しなくなります。この部分を飽和領域と呼んでいます。
三相短絡曲線
三相同期発電機の三つの端子を短絡させ、定格速度で回転している場合の、界磁電流\(I_f\)[A]と短絡電流\(I_s\)[A]の関係を示したものを「三相短絡曲線」といいます。
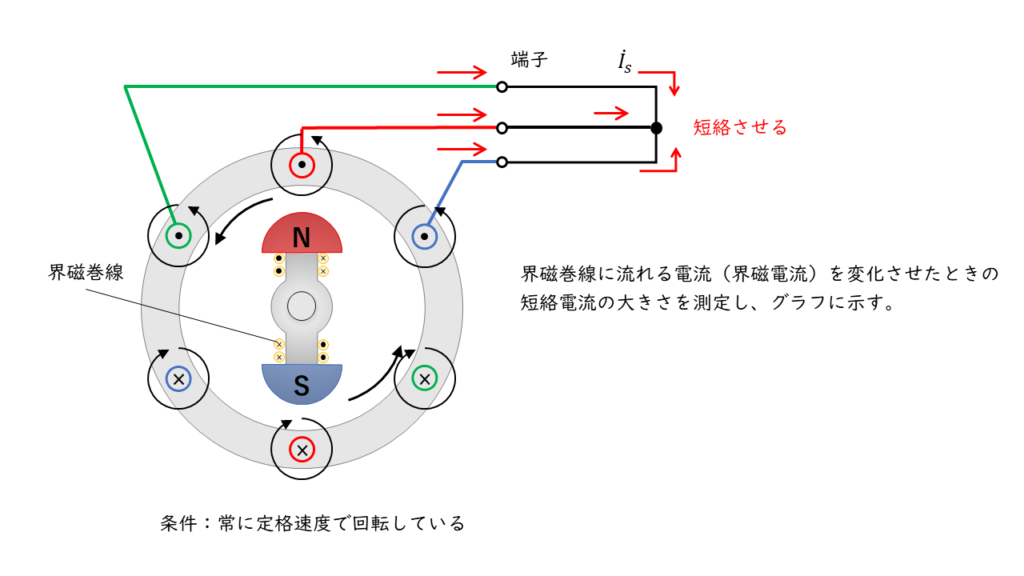
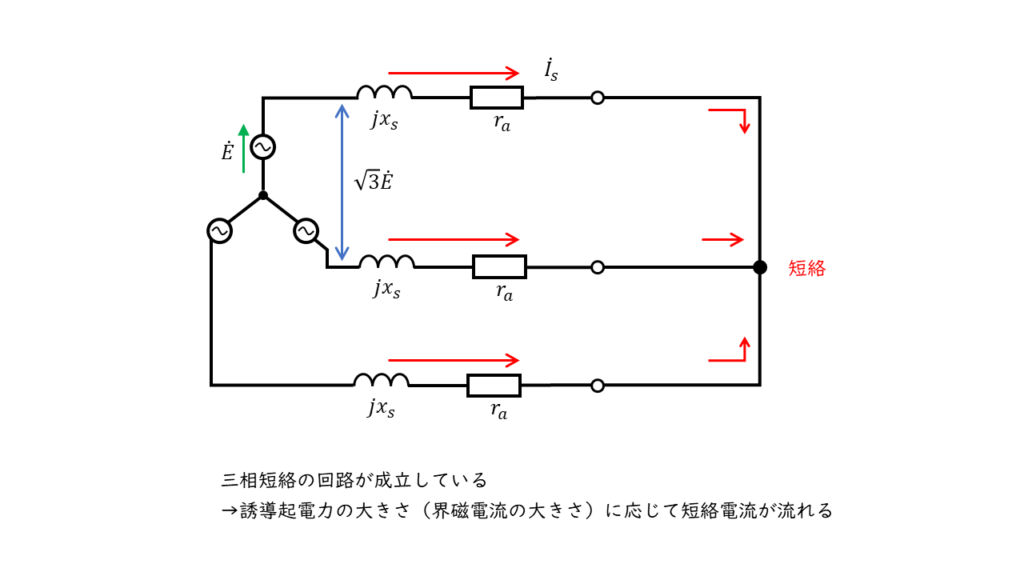
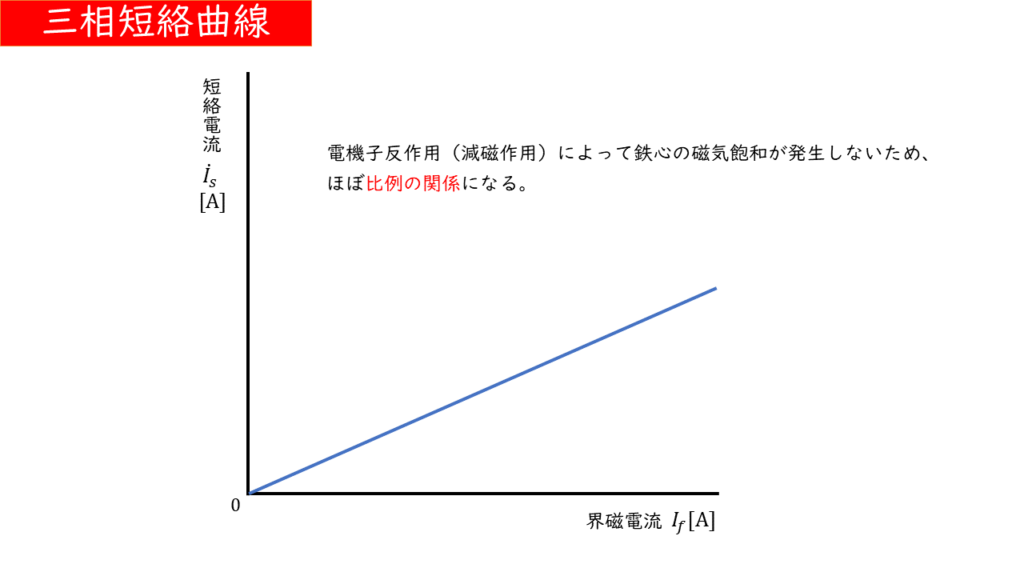
同期リアクタンスは電気子巻線抵抗よりかなり多きため、電機子反作用は減磁作用として働きます。
その結果、鉄心の磁気飽和が起こらないため、短絡電流と界磁電流はほぼ比例の関係となり、グラフは直線を示します。
短絡比と同期インピーダンス
短絡比
無負荷で定格電圧\(V_n\)[V]を発生させる界磁電流\(I_{fs}\)[A]と、定格電流\(I_n\)[A]と等しい三相短絡電流を発生させる界磁電流\(I_{fn}\)[A]の比を短絡比と呼びます。
短絡比:\( K_s = \displaystyle \frac{I_{fs}}{I_{fn}} \)
短絡比は、同期発電機の特性の中でも特に重要な定数で、発電機の安定度や線路充電容量と深くかかわりがあります。そのため、電験三種の試験でも特に頻出の内容です。
短絡比の計算に必要な界磁電流\(I_{fs} \)と\(I_{fn}\)は先ほどまでに学習した、「無負荷飽和曲線」と「三相短絡曲線」から読み取ることができます。
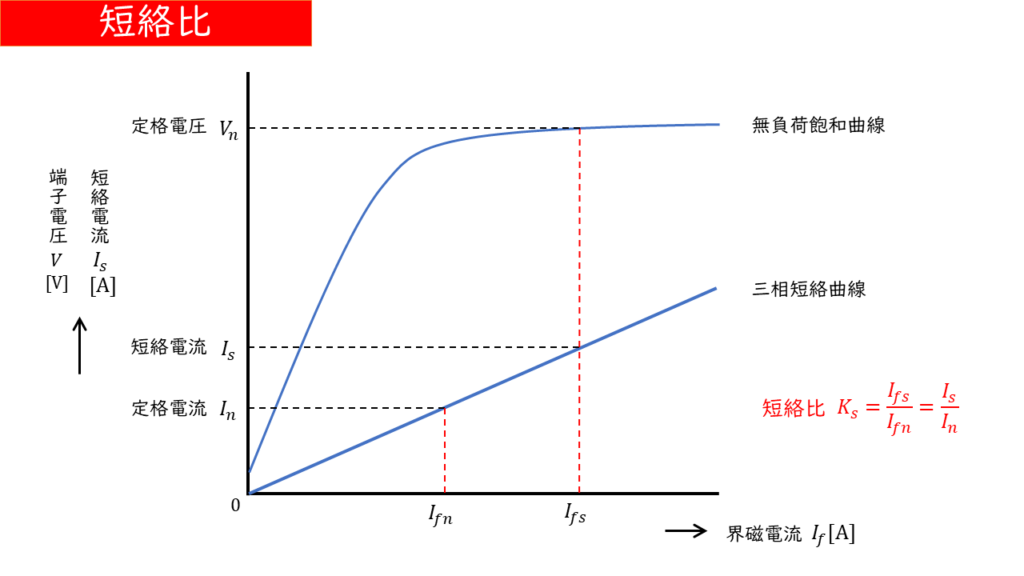
また、短絡比は定格電流に対して何倍の三相短絡電流が流れるかを表した比と考えることもできます。したがって、短絡比の公式は以下のようになります。
短絡比:\( K_s = \displaystyle \frac{I_{fs}}{I_{fn}} = \displaystyle \frac{I_s}{I_n} \)
短絡比の値は、発電機が接続される系統を考慮して選定されており、同期発電機の代表的なもので圧水車発電機では0.8~1.0、タービン発電機では0.5~0.7の値が竿用されています。
短絡比の大きさによって、同期機には次のような特徴があります。
| 短絡比 | 同期インピーダンス | 短絡電流 | 電圧変動率 | 鉄機械or銅機械 |
| 大きい | 小さい(電機子反作用が小さい) | 大きい | 小さい | 鉄機械と呼ばれる(鉄を多く使用するから) |
| 小さい | 大きい(電機子反作用が大きい) | 小さい | 大きい | 銅機械と呼ばれる |
同期インピーダンス
同期発電機の同期リアクタンスと電機子巻線抵抗を合わせたものを同期インピーダンスと呼びました。
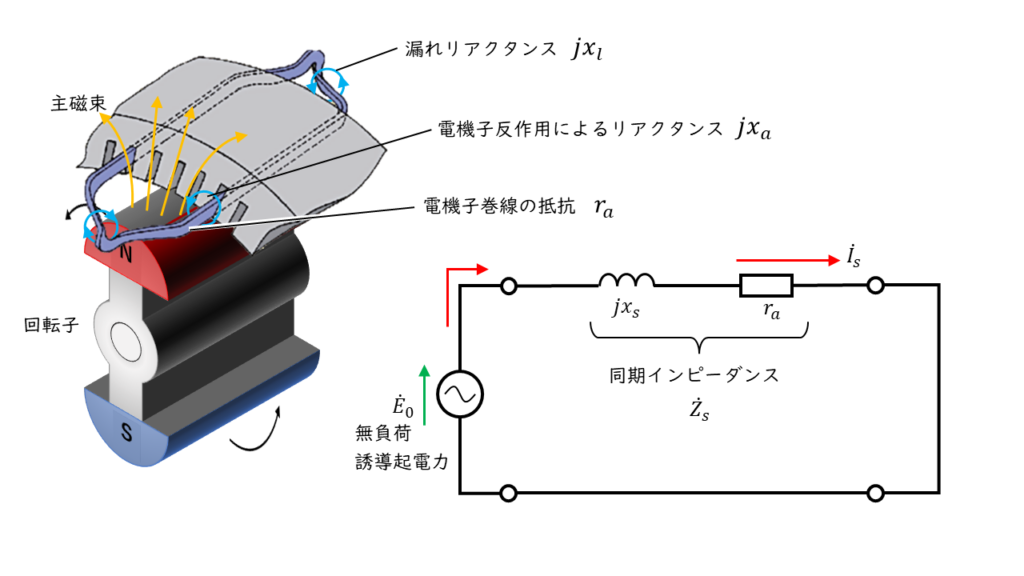
上図の等価回路のように、定格相電圧\(E_n\)[V]が印加された状態で、短絡したときに流れた短絡電流を\(I_s\)[A]と置きます。この時、同期インピーダンスは、
同期インピーダンス:\(Z_s = \displaystyle \frac{E_n}{I_s} = \displaystyle \frac{V_n}{\sqrt{3} I_s} \)
発電機や変圧器のインピーダンスは電力系統の短絡電流を計算しやすいように%単位で表されることが多いです。
同期インピーダンスを\(\Omega\)単位から%単位に変換したものを「百便率同期インピーダンス」またはと言い、記号は%\(Z_s\)で表します。
\( \begin{align} \% Z_s &= \displaystyle \frac{Z_s I_n}{E_n} \times 100 \\ \\ &= \displaystyle \frac{Z_s I_n}{\displaystyle \frac{V_n}{ sqrt{3} }} \times 100 \\ \\ &= \frac{\sqrt{3} Z_s I_n}{V_n} \times 100 [\rm \%] \end{align} \)
【関連記事】
短絡比と百分率同期インピーダンス
短絡比と百分率同期インピーダンスの間には、次のような関係が成り立ちます。
短絡比:\( K_s = \displaystyle \frac{I_{fs}}{I_{fn}} = \frac{100}{\% Z_s} \)
短絡比と百分率インピーダンスの関係式の導出
百分率同期インピーダンスの公式より、
\( \begin{align} \% Z_s &= \displaystyle \frac{Z_s I_n}{E_n} \times 100 \\ &= \displaystyle \frac{I_n}{\frac{E_n}{Z_s}} \times 100 \\ &= \displaystyle \frac{I_n}{I_s} \times 100 \end{align} \)
よって、短絡比\( K_s = \displaystyle \frac{I_s}{I_n} \)は、
\( K_s = \displaystyle \frac{I_s}{I_n} = \displaystyle \frac{100}{%Z_s} \)
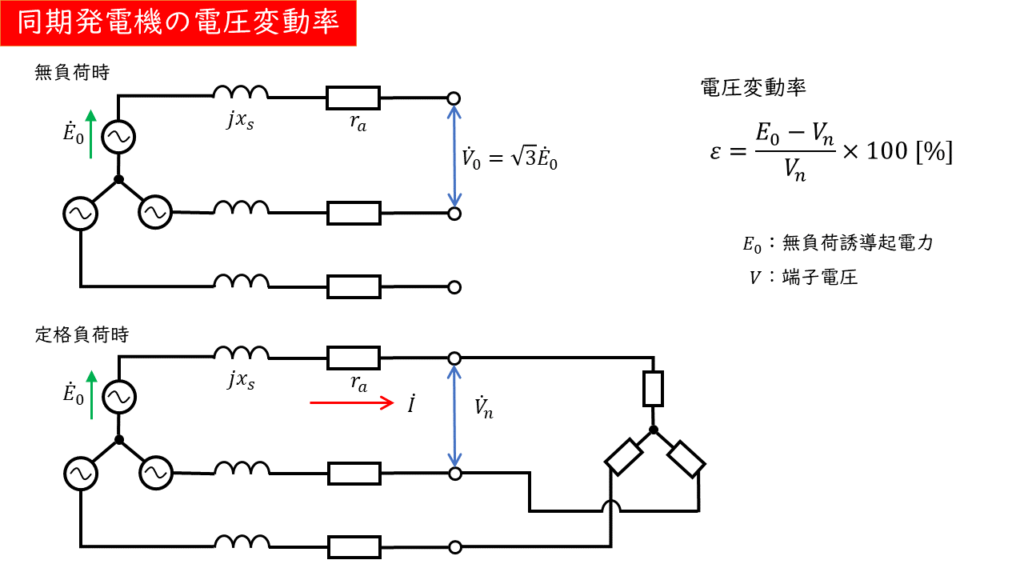
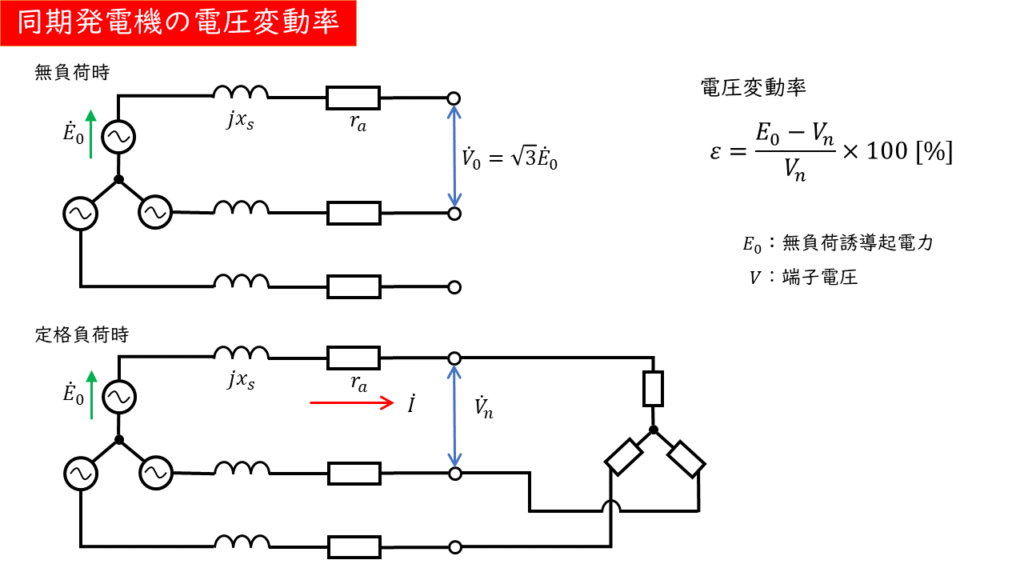
同期発電機の電圧変動率
三相同期発電機の端子電圧は、電気子反作用等の同期リアクタンスによる影響を受けるため無負荷誘導起電力がそのまま出てくることはありません。
そこで、定格端子電圧を基準にして、定格負荷から無負荷に変化したとき、どのくらい電圧の値が変化するかを表したものが電圧変動率です。
電圧変動率:\( \epsilon = \displaystyle \frac{無負荷誘導起電力\ E_0 – 定格端子電圧\ V_n}{定格端子電圧\ V_n} \times 100\)[%]
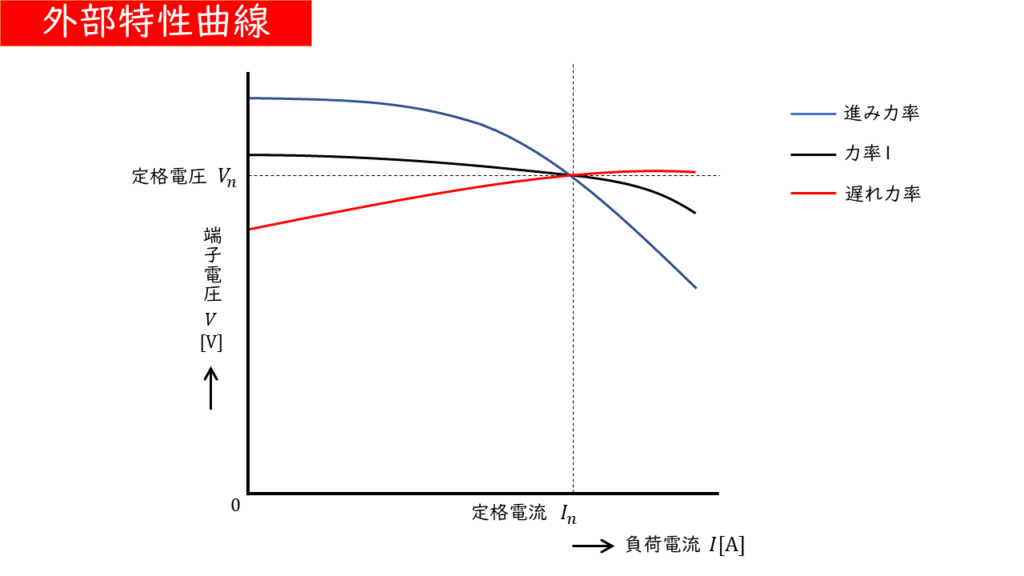
外部特性曲線
回転速度と界磁電流と負荷力率\(\cos \theta\)を一定に保ち、負荷電流\(I\)[A]を変化させたときの端子電圧\(V\)[V]の値を示したものを「外部位相特性曲線」といいます。
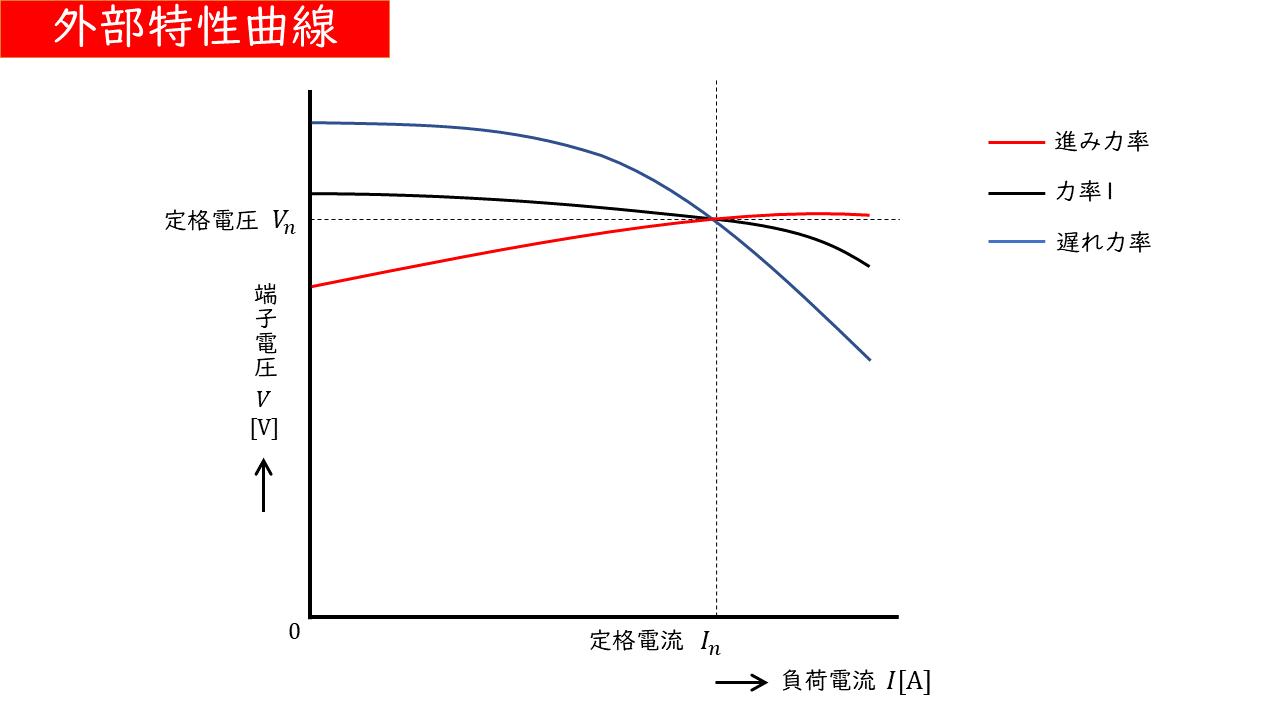
力率が1の場合
負荷電流が大きくなっても、端子電圧はわずかに低下するだけです。この減少は、電機子巻線抵抗による電圧降下の影響です。
遅れ力率の場合
減磁作用の影響が大きくなるため、負荷電流が大きくなると端子電圧は大きく低下します。
進み力率の場合
増磁作用の影響が大きくなるため、負荷電流が大きくなると、端子電圧が上昇します。
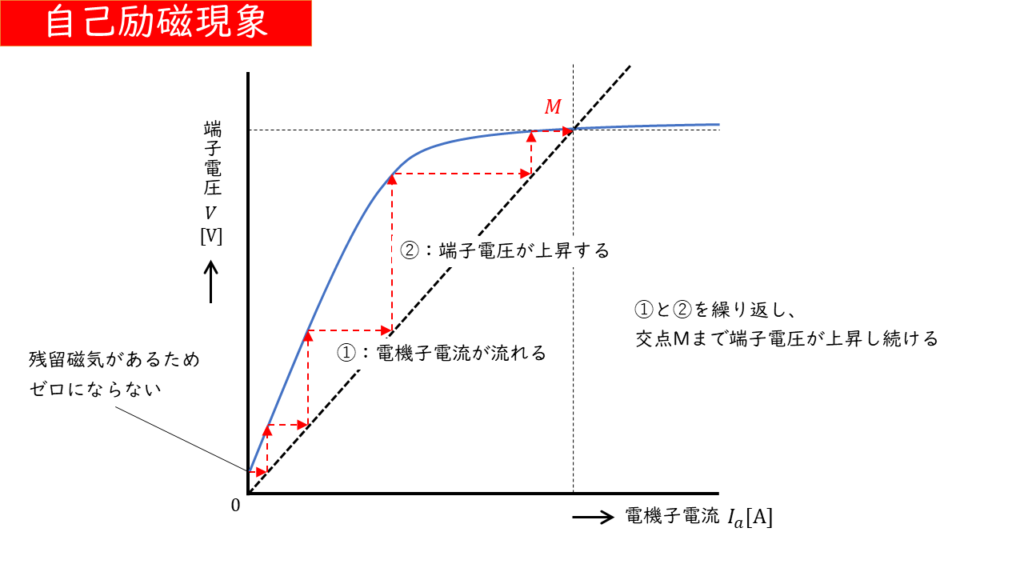
自己励磁現象
同期発電機が容量負荷(無負荷の長距離高圧送電線路)に接続されている場合、自己励磁現象が発生します。
【自己励磁現象の流れ】
- 残留磁気によって小さな電圧が発生します
- 電機子に進み電流が流れます
- 進み電流によって増磁作用が起こり、さらに端子電圧が上昇します
- 端子電圧が上昇することで、さらに大きな進み電流が流れます
- 1~4を繰り返し、グラフの交点Mまで端子電圧が上昇します
交点Mが定格電圧よりも大きい場合、巻線の絶縁を脅かす危険があります
まとめ




過去の出題実績
H12年度 問2
H15年度 問4、問5
H16年度 問5
H18年度 問3
H19年度 問5
H20年度 問4
H21年度 問5
H24年度 問6
H25年度 問6
H27年度 問4、問5
H29年度 問5
R3年度 問6
R4年度上期 問5
R4年度下期 問5








コメント