磁界と電流・電圧の関係性を理解するうえで「電磁誘導」、「誘導起電力」の理解は重要です。
また、誘導起電力はコイルを利用する様々な電気機器で利用されています。電験3種 理論科目はもちろんのこと、機械科目における変圧器や誘導機、同期機などを理解するうえでも非常に重要な基礎知識です。
誘導起電力の原理的な内容を問われる問題は少ないですが、全ての科目に通じる基礎的内容です。
図を見ながら、どのような現象が発生しているのか理解を深めていきましょう。
- 電磁誘導とは
- 誘導起電力の大きさ
- 誘導起電力の向き
(フレミングの右手の法則) - 磁界の中を動く導体に生じる誘導起電力
電磁誘導とは
図のようにコイルに磁石を近づけたり遠ざけたりすると、コイルに電圧(起電力)が生じ電流が流れます。
この現象を電磁誘導と呼びます。
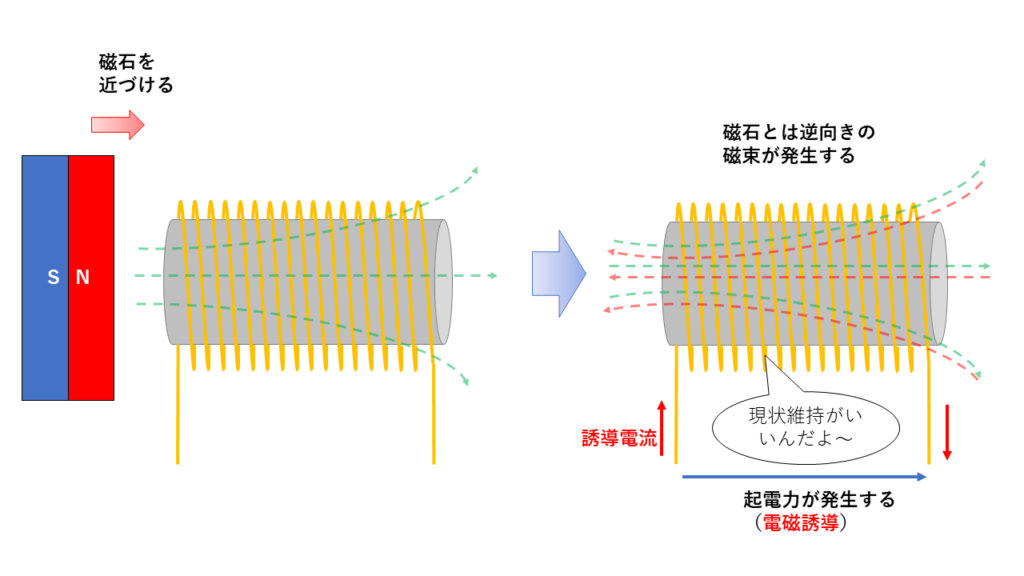
この時に生じる電圧を誘導起電力といい、流れる電流を誘導電流といいます。
誘導起電力の大きさ
誘導起電力の大きさは、コイルの内部を貫く磁束の単位時間\(\Delta t\)[s]あたりの変化に比例します。(ファラデーの法則)
また、コイルは磁束の変化を嫌うので、磁束の変化を妨げる向きに磁界を発生させるような誘導起電力が生じます。(レンツの法則)
$$誘導起電力 e= -N \frac{\Delta \phi}{\Delta t}[V]$$
Nはコイルの巻数を表し、巻き数が多いほど誘導起電力も大きくなります。
また、コイルと鎖交(コイルの中を通り抜ける)する磁束の数を磁束鎖交数(\(N\phi\)といいます。
Δとは変化分を表すときに使用する記号です。
もう少し詳しく順を追って、誘導起電力が発生するまでの流れを見てみましょう!
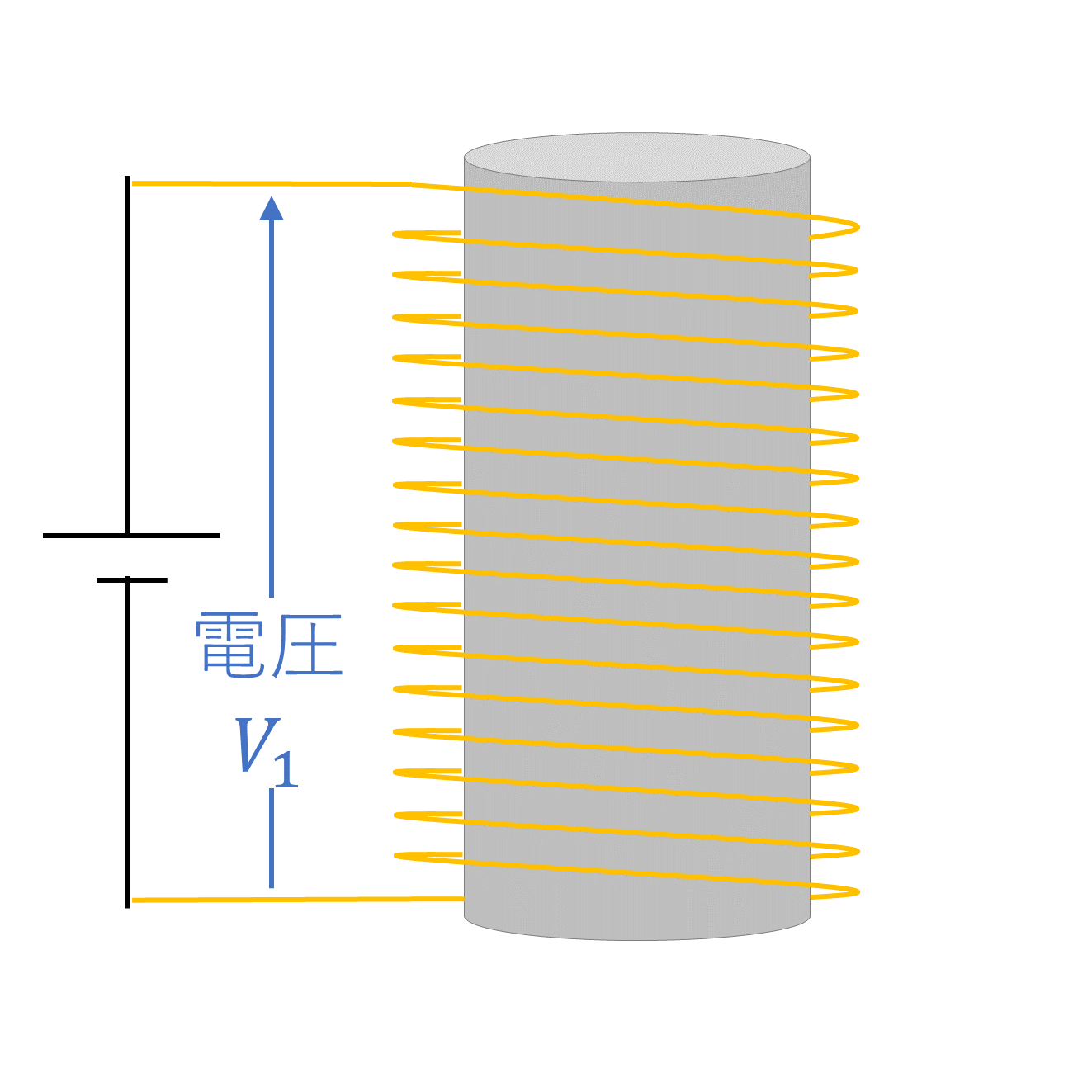
- コイルに電圧を印加する

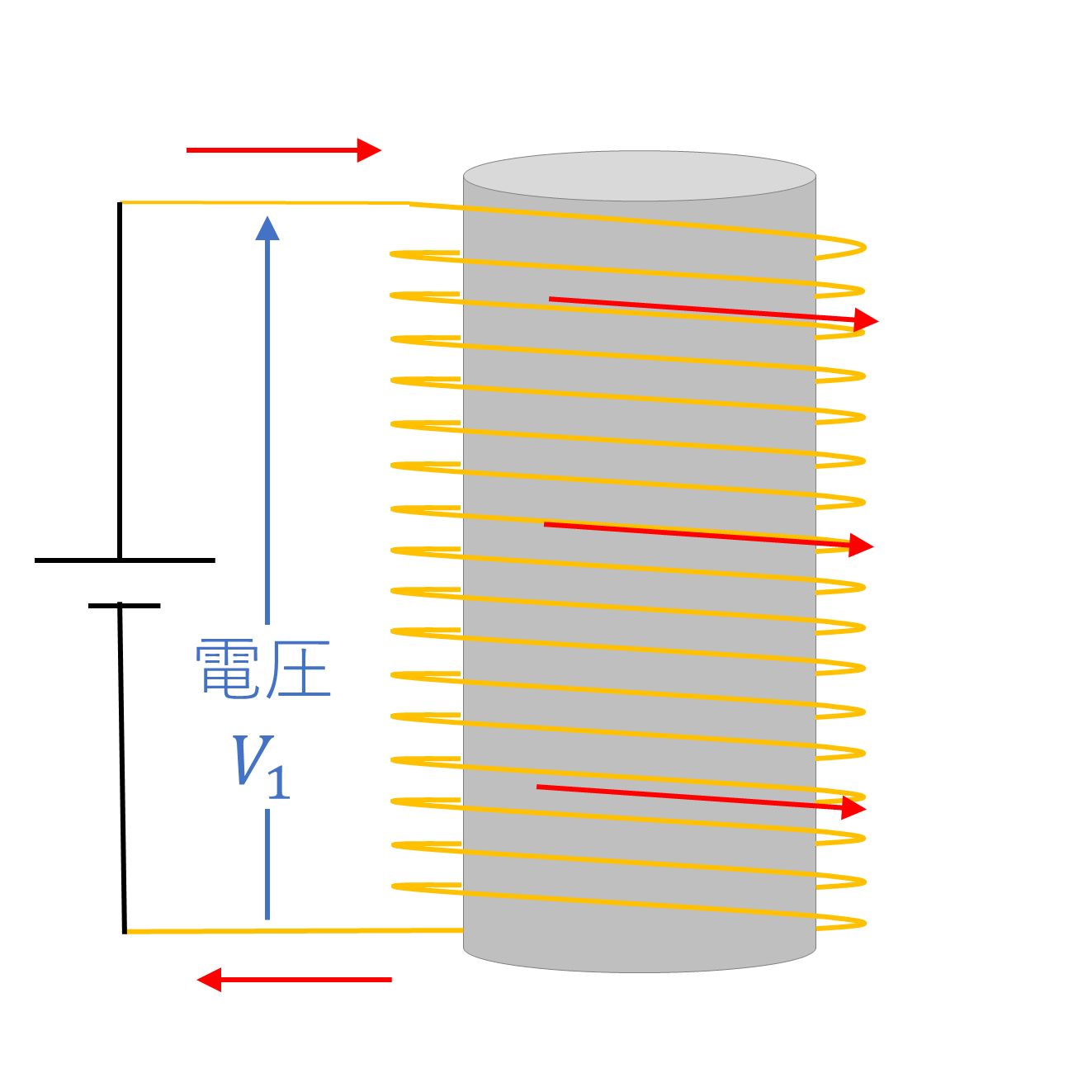
- コイルに電流が流れる

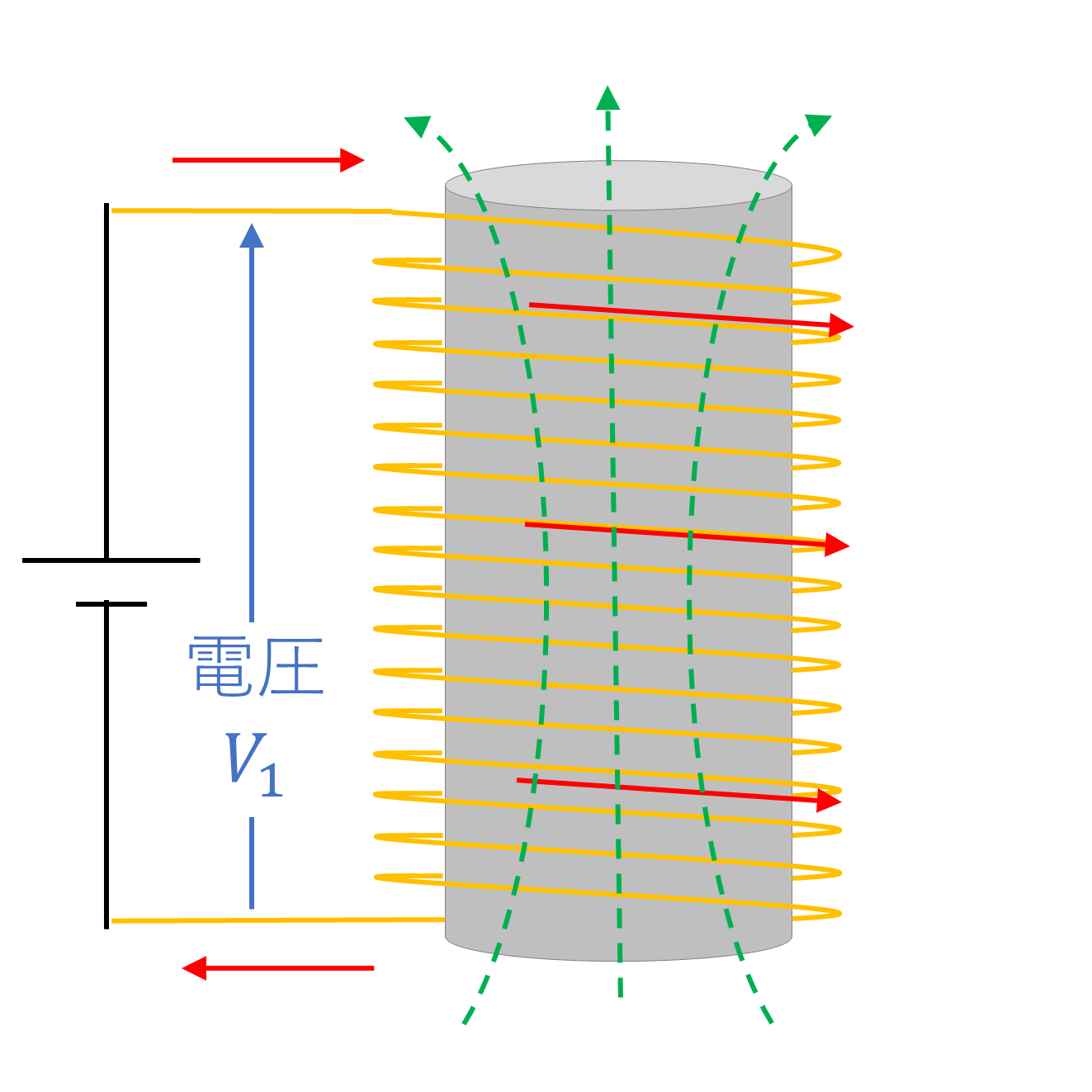
- コイルを流れる電流は、右ねじの法則にしたがい磁束を発生させる

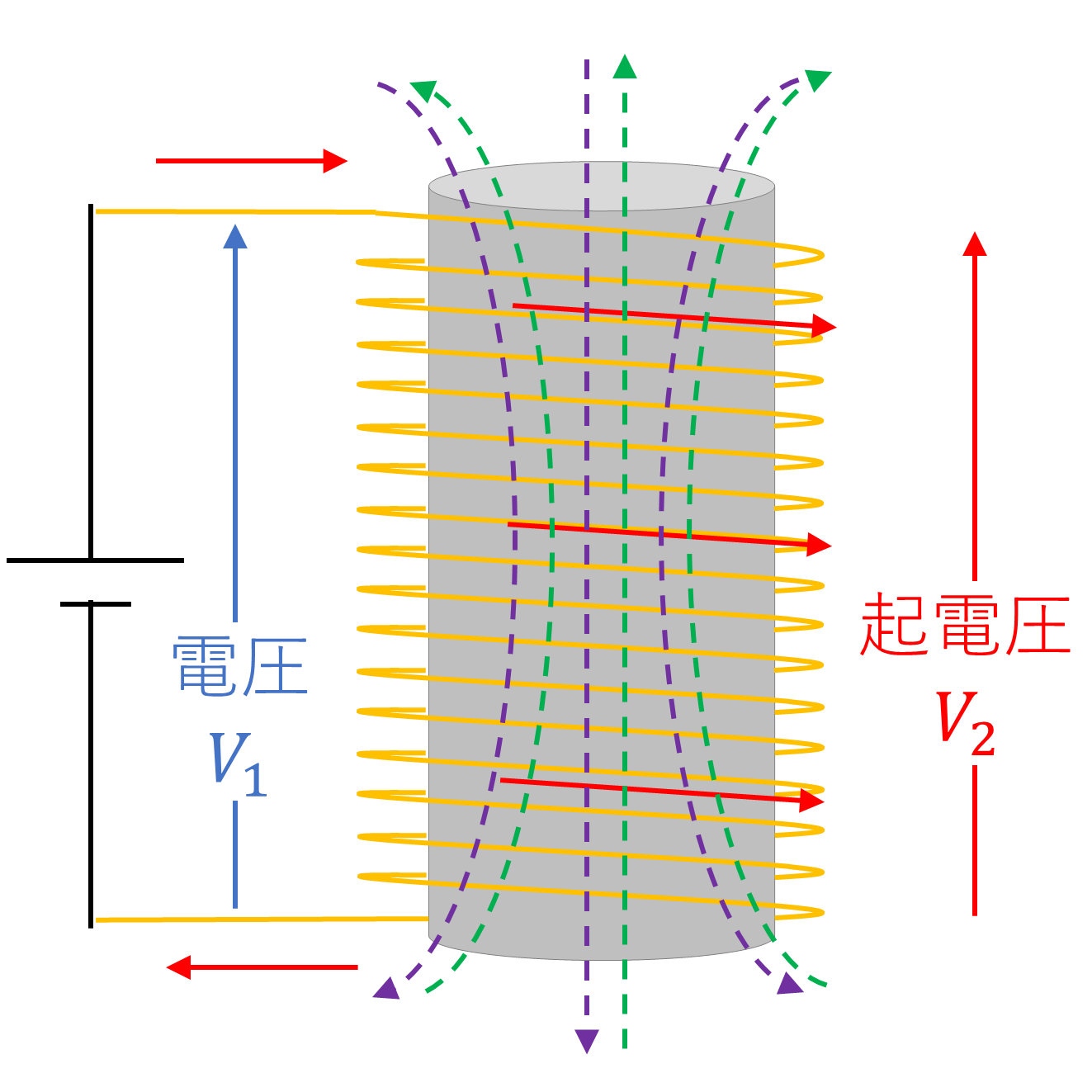
- コイルは磁束の変化を嫌うので、磁束の変化とは逆向きの磁束を作る誘導起電力がコイルに発生する

誘導起電力の向き
誘導起電力の向きはフレミングの右手の法則によって求めることができます。
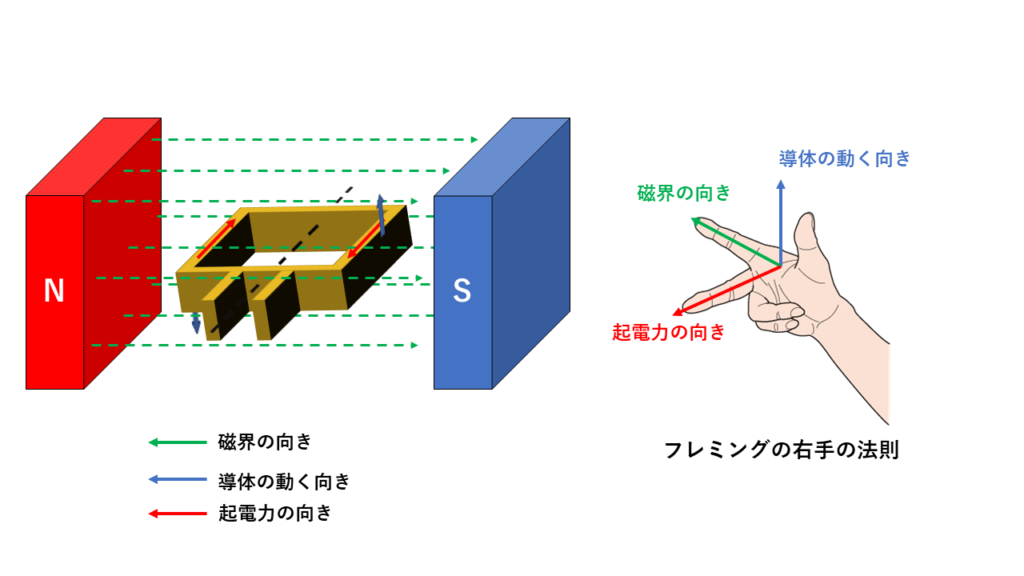
磁界の中を動く導体に生じる誘導起電力
平面上を運動する場合
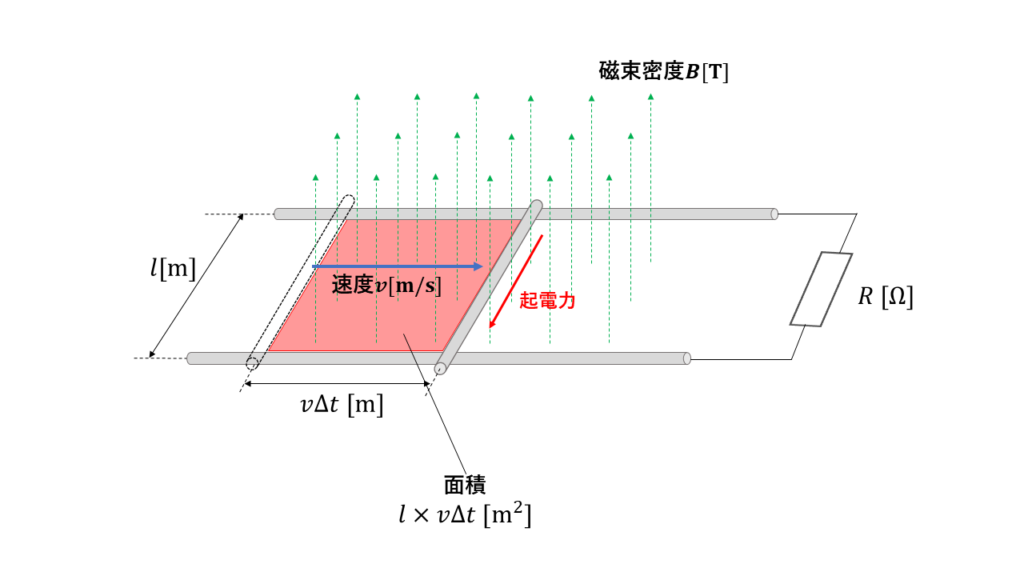
図のように2本の平行な導体棒でできたレールのうえを、長さ\(l\)[m]の導体が速度\(v\)[m/s]で移動するとき、1回巻きの大きなコイルと考える。
\(\Delta t\)[s]間に導体は\(v\Delta t\)[m]だけ移動するので、コイルを貫く磁束の数は
$$\Delta\phi=B \times l\times v\Delta t$$
だけ現象する。
よってこの時に生じる誘導起電力\(e\)[V]は
$$\begin{align}e=-N\frac{\Delta \phi}{\Delta t}=-N\frac{(-B\times l\times v\Delta t)}{\Delta t}=Blv [V]\end{align}$$
と求めることができます。
導体が磁束を斜めに通過するとき
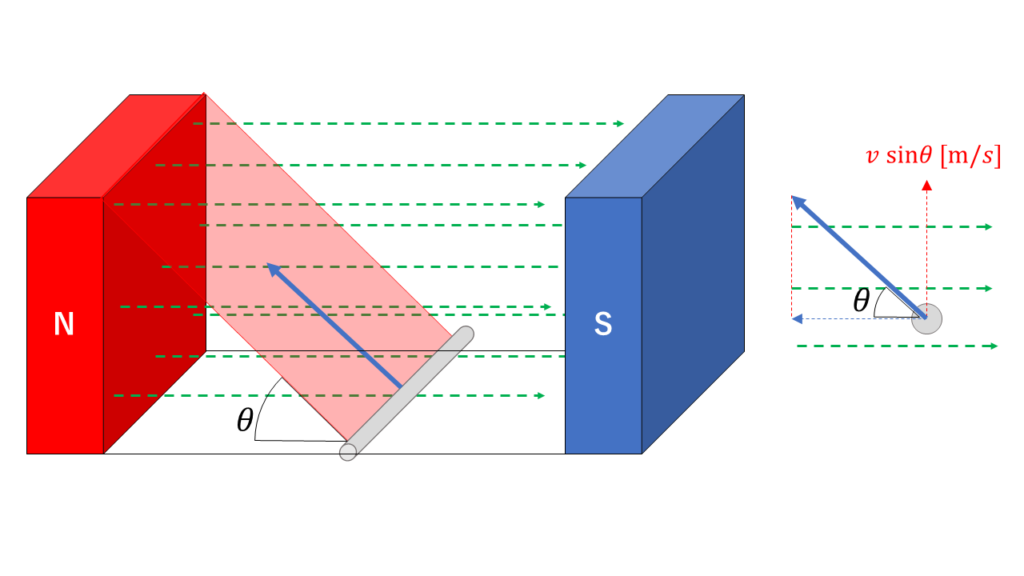
誘導起電力は、導体の運動する向きに直角に交わる磁束が影響していました。(フレミングの右手の法則)
したがって、運動の向きを磁束と直角な向きに分解する必要があります。
磁束中を運動する導体に生じる誘導起電力の公式は次のように表すことができます。
$$e=B\times l\times vsin\theta$$
まとめ
電磁誘導でポイントになるのは以下の点です。

基本の式に忠実な問題が多いので、公式の意味を理解して使いこなそう!








コメント