問題
環状鉄心に,コイル \(1\) 及びコイル \(\) 2が巻かれている。二つのコイルを図1のように接続したとき,端子 \(\rm A−B\) 間の合成インダクタンスの値は \(1.2\ \rm H\) であった。次に,図2のように接続したとき,端子 \(\rm C−D\) 間の合成インダクタンスの値は \(2.0\ \rm H\) であった。このことから,コイル \(1\) の自己インダクタンス \(L\) の値 \(\rm [H]\) ,コイル \(1\) 及びコイル \(2\) の相互インダクタンス \(M\) の値 \(\rm [H]\) の組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
ただし,コイル \(1\) 及びコイル \(2\) の自己インダクタンスはともに \(L\ \rm [H]\) ,その巻数を \(N\) とし,また,鉄心は等断面,等質であるとする。

$$ \begin{array}{ccc} \ & 自己インダクタンス L & 相互インダクタンス M \\ \hline (1) & 0.4 &0.2 \\ \hline (2) & 0.8 & 0.2 \\ \hline (3) & 0.8 &0.4 \\ \hline (4) & 1.6 &0.2 \\ \hline (5) & 1.6 & 0.4 \\ \hline \end{array} $$
解説
答え:(2)
図 \(1\) ,図 \(2\) の接続の種類を判別する
同一鉄心上に巻かれた2つのコイルの接続方法には,「和同接続」と「差動接続」の2つがあります。
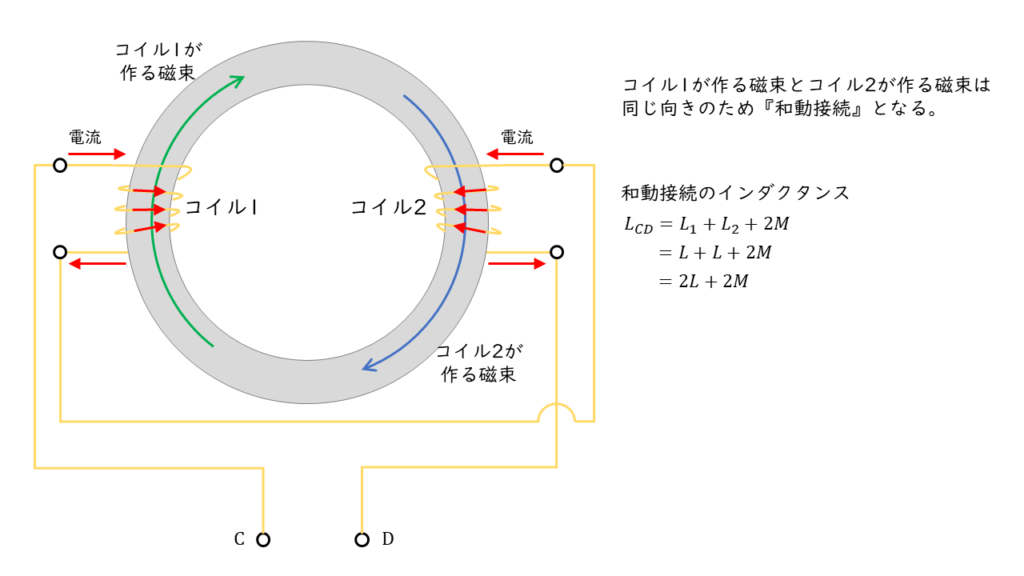
「和同接続」とは,2つのコイルが作る磁束の向きが同じになり,磁束を強めあう接続方法です。
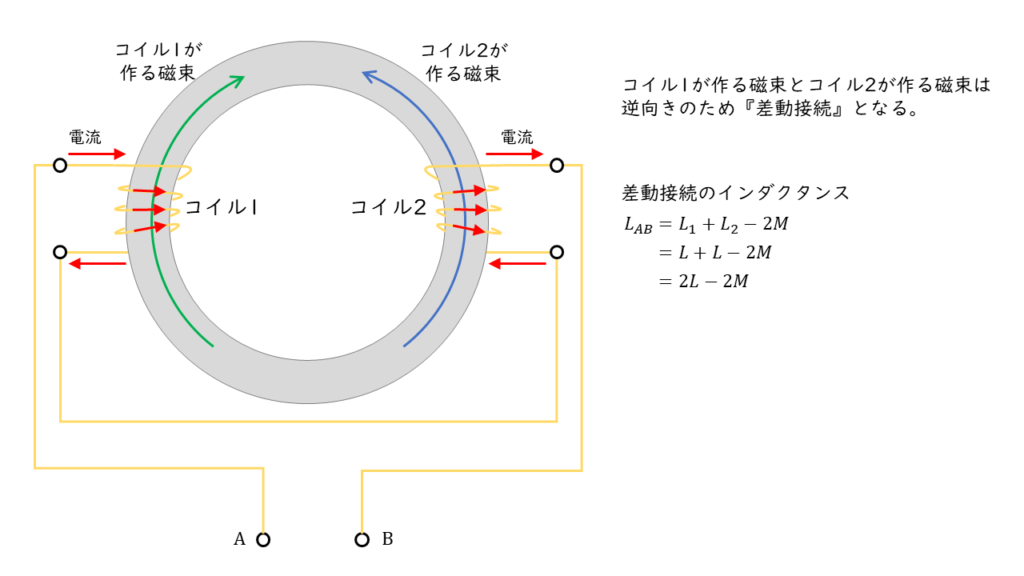
「差動接続」とは,2つのコイルが作る磁束の向きが逆向きになり,磁束を打ち消しあうような接続方法です。
問の図 \(1 , 2\) から,それぞれの接続方法は,
図 \(1\):差動接続
図 \(2\):和同接続
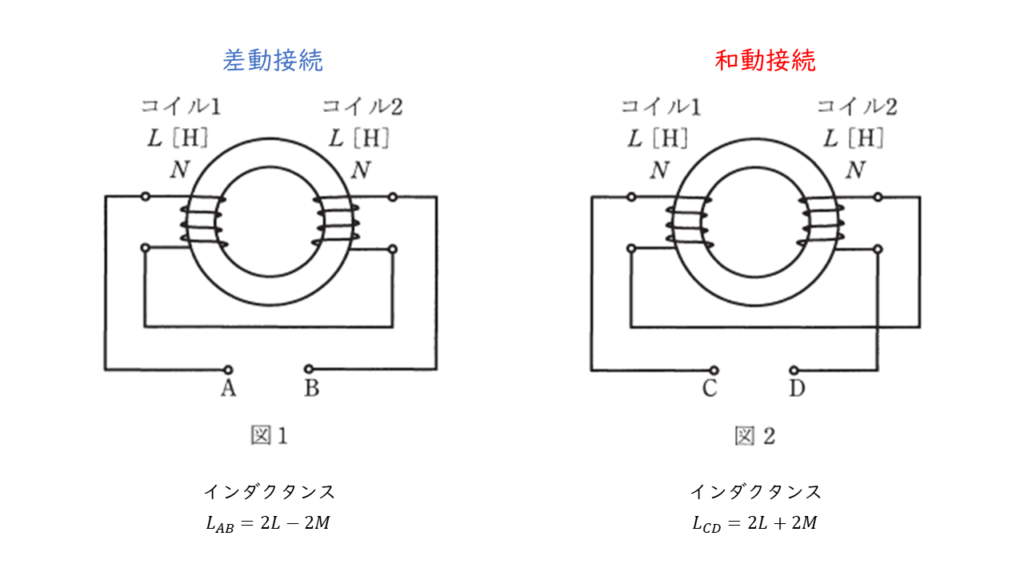
となります。
和同接続,差動接続のインダクタンスの公式を連立して解く
図 \(1 , 2\) から,自己インダクタンスを \(L\) ,相互インダクタンスを \(M\) とすると,
図 \(1\) 差動接続の場合
\( L_{12} = L + L -2M = 2L-2M =1.2 \)
図 \(2\) 和動接続の場合
\( L’_{12} = L + L +2M = 2L+2M =2.0 \)
と2つの式が成り立ちます。この2式を連立して解き,自己インダクタンス \(L\) と相互インダクタンス \(M\) を計算すると,
\(\begin{align} 2L \ – \ 2M &= 1.2 \\ – ) 2L + 2M &= 2.0 \\ \hline 4L \ &=3.2 \\ L \ &=0.8\end{align} \)
となります。また,自己インダクタンス \(L\) の値を和同接続のインダクタンスの式に代入し相互インダクタンス \(M\) を計算すると,
\(\begin{align} L’_{12} = 2L+2M &= 2.0 \\ 2 \times 0.8 + 2M &= 2.0 \\ 2M &= 2.0-1.6 \\ 2M &= 0.4 \\ M &= 0.2 \end{align} \)
以上の計算結果から,
自己インダクタンス:\( L = 0.8 \ \rm [H]\)
相互インダクタンス:\( M = 0.2 \ \rm [H] \)
と計算できるので,答えは(2)となります。











コメント