問題
図のように,三つの抵抗 \(R_1\ [\Omega]\) , \(R_2\ [\Omega]\) , \(R_3\ [\Omega]\) とインダクタンス \(L\ \rm [H]\) のコイルと静電容量 \(C\ \rm [F]\) のコンデンサが接続されている回路に \(V\ \rm [V]\) の直流電源が接続されている。定常状態において直流電源を流れる電流の大きさを表す式として,正しいものを次の(1)~(5)のうちから一つ選べ。
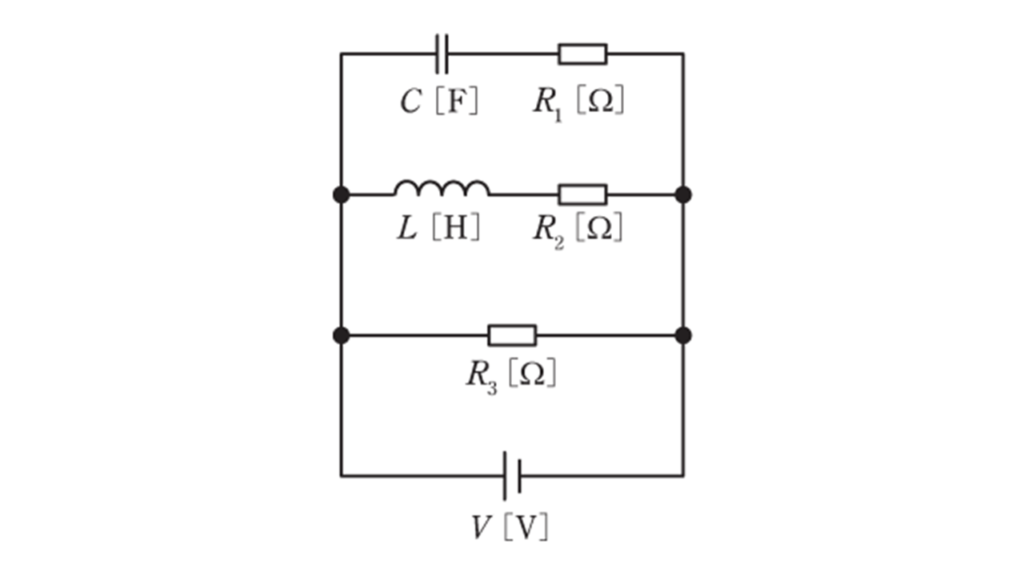
(1) \(\displaystyle \frac{V}{R_3}\) (2) \(\displaystyle \frac{V}{\displaystyle \frac{1}{\displaystyle \frac{1}{R_1} + \displaystyle \frac{1}{R_2}}} \) (3) \(\displaystyle \frac{V}{\displaystyle \frac{1}{\displaystyle \frac{1}{R_1} + \displaystyle \frac{1}{R_3}}} \)
(4) \(\displaystyle \frac{V}{\displaystyle \frac{1}{\displaystyle \frac{1}{R_3} + \displaystyle \frac{1}{R_3}}} \) (5) \(\displaystyle \frac{V}{\displaystyle \frac{1}{\displaystyle \frac{1}{R_1} + \displaystyle \frac{1}{R_2} + \displaystyle \frac{1}{R_3}}} \)
解説
答え:(4)
直流回路の定常状態におけるコイルとコンデンサの働き
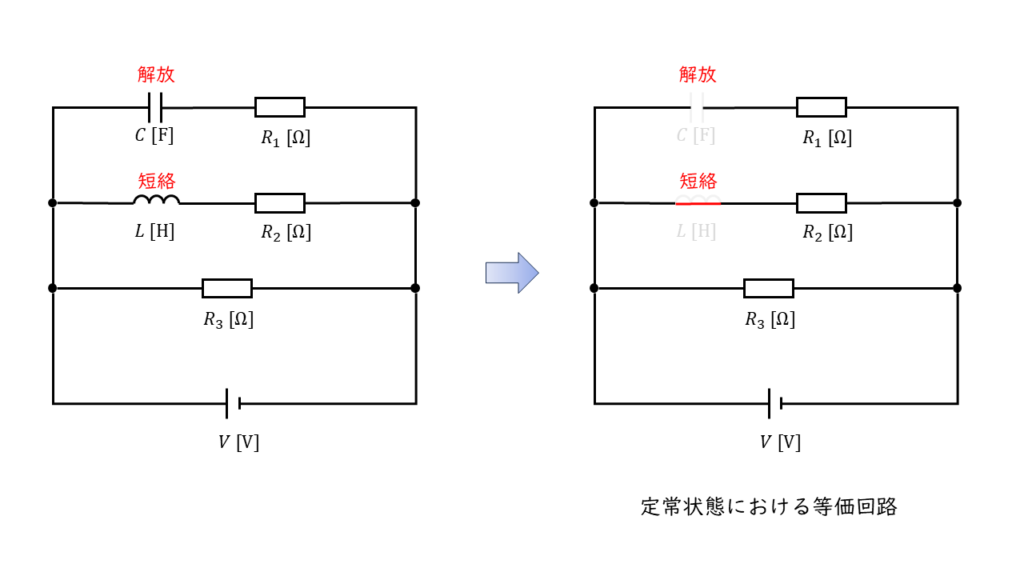
定常状態(電源と接続されてから十分に時間が経った状態)では,コイルとコンデンサはそれぞれ次のように扱うことができます。
コイル \(L\) :定常状態では,「短絡」とみなす
コンデンサ \(C\) :定常状態では,「解放」とみなす
よって,問いの回路図は,定常状態では以下のような回路図と考えることができます。
定常状態における回路全体を流れる電流を計算する
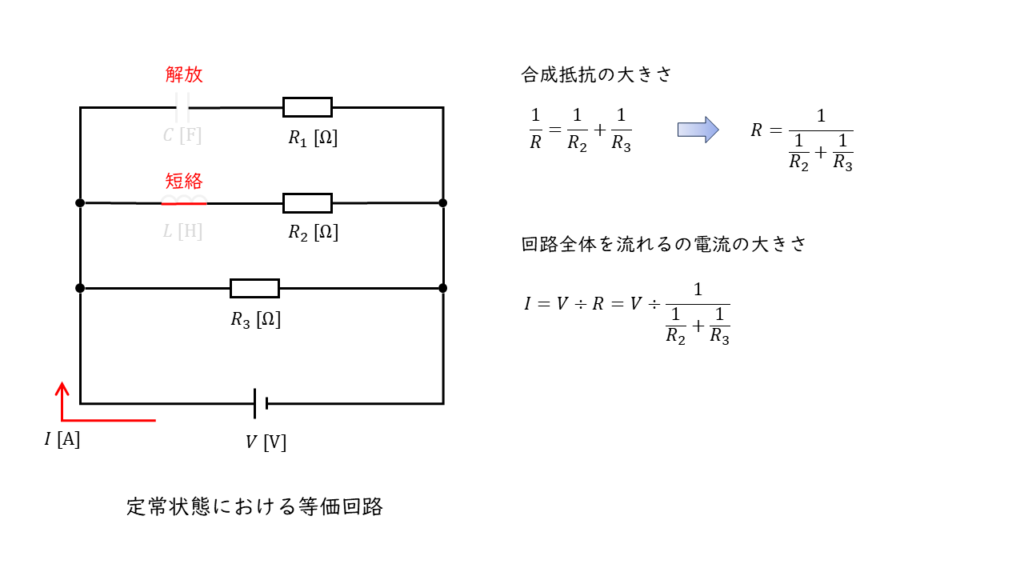
図より,抵抗 \(R_1\) は「解放状態」,抵抗 \(R_2\) ,\(R_3\) は電源と並列に接続された状態と考えられるので,回路全体を流れる電流 \(I\ \rm[A]\) の大きさは,
\(\begin{align} I &= V \div \left( \displaystyle \frac{1}{ \displaystyle \frac{1}{R_2} + \displaystyle \frac{1}{R_3} }\right) \\ \\ &= \displaystyle \frac{V}{\displaystyle \frac{1}{\displaystyle \frac{1}{R_3} + \displaystyle \frac{1}{R_3}}} \end{align} \)
したがって、答えは(4)となります。










