問題
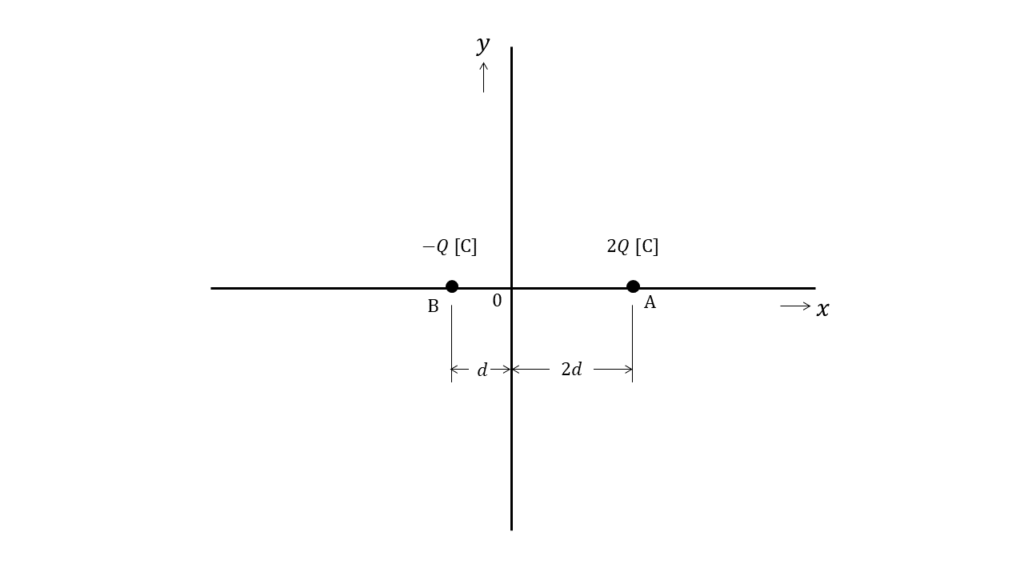
真空中において,図のように\(x\)軸上で距離\(3d\ \rm[m]\)隔てた点\(A(2d,0)\) ,点\(B(−d,0)\)にそれぞれ\(2Q\ \rm[C]\),\(−Q\ \rm[C]\)の点電荷が置かれている。\(xy\)平面上で電位が\(0\ V\)となる等電位線を表す図として,最も近いものを次の\((1)~(5)\)のうちから一つ選べ。
解説
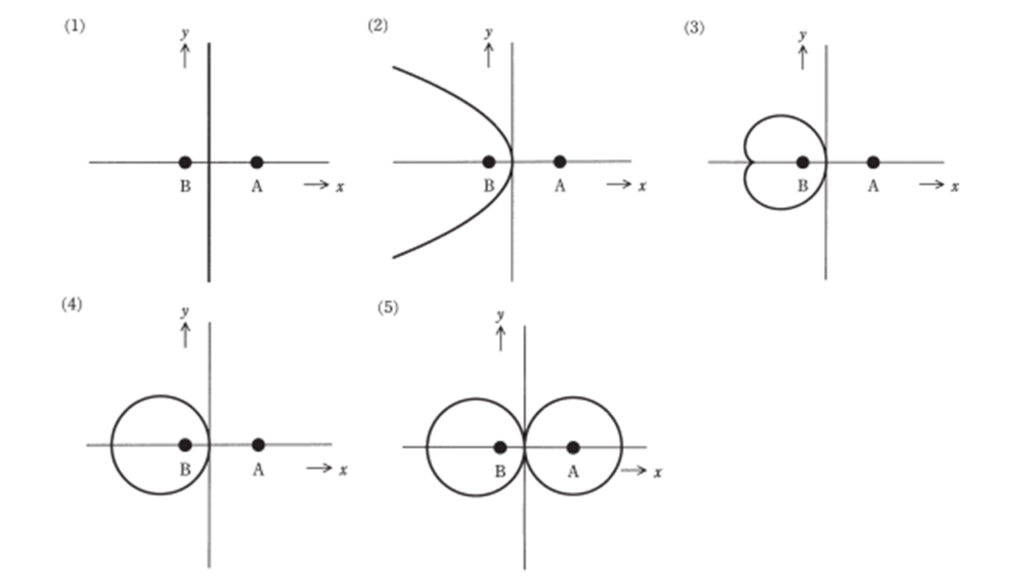
答え:(4)
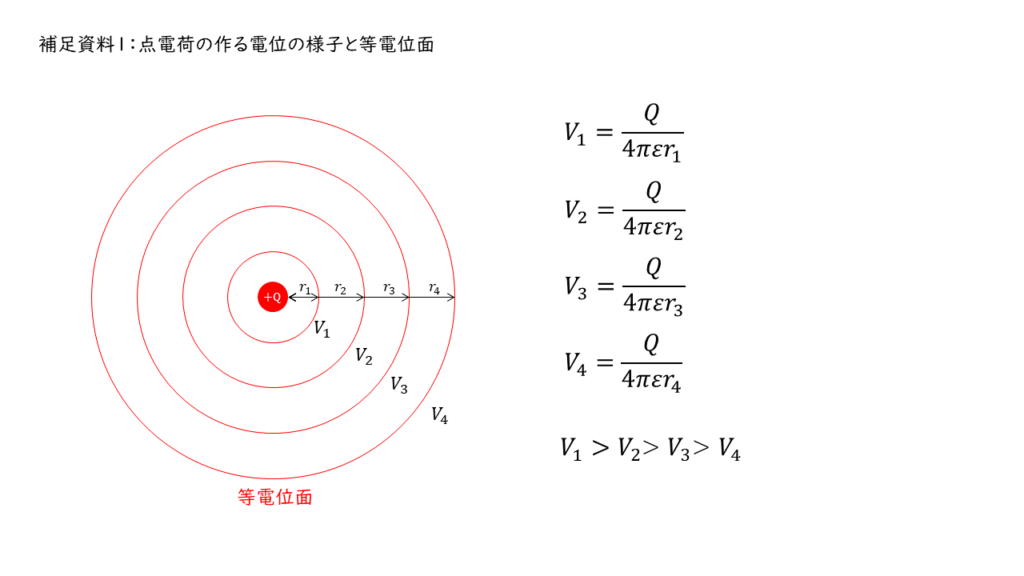
各点電荷の作る電位の大きさを式で表す
点電荷の作る電位の大きさは以下の式となる。
\( V = \displaystyle \frac{Q}{4 \pi ε r} \)
点電荷\(A\),\(B\)の作る電位の大きさは,点電荷からの距離をそれぞれ\(r_A\),\(r_B\)とすると
\( V_A = \displaystyle \frac{2Q}{4 \pi ε r_A} \\ V_B =\displaystyle \frac{-Q}{4 \pi ε r_B} \)
と表すことができる。
ここで、点電荷\(A\),\(B\)の作る電位の和が\(0\ V\)となる点を\(P\ (x,y) \)と置く。
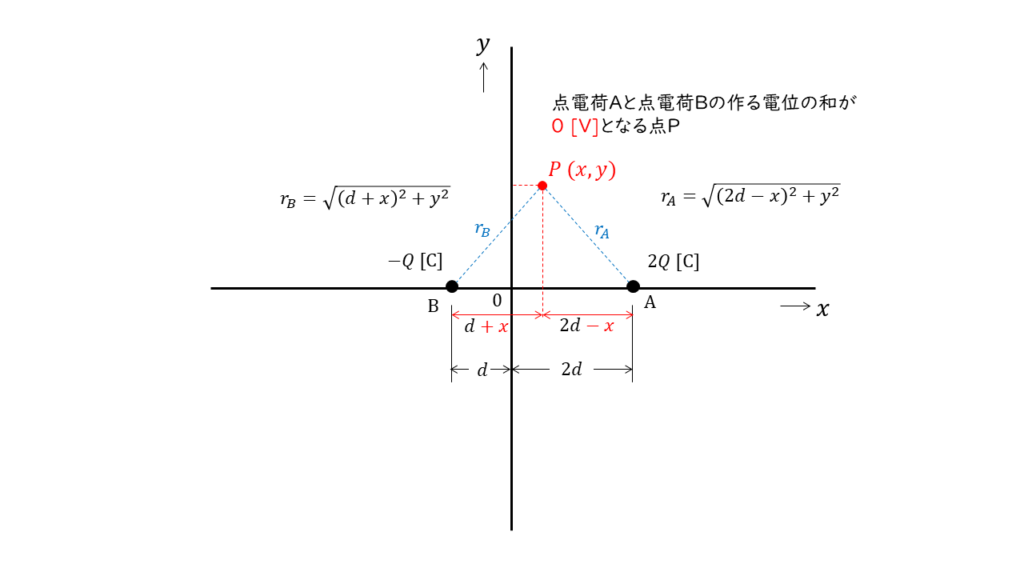
この時の電位\(V_A\),\(V_B\)の式は以下の様に表される。
\( V_A = \displaystyle \frac{2Q}{4 \pi ε \sqrt{\left( 2d-x \right)^2 + y^2}} \\ V_B = \displaystyle \frac{-Q}{4 \pi ε \sqrt{ \left(d+x \right)^2 + y^2}} \)
電位の合計が0 Vとなる点を求める
2つの電位の合計が\(0\ V\)となるので,
\( \begin{align} V_A + V_B &= 0 \\ \\ \frac{2Q}{4 \pi ε \sqrt{\left( 2d-x \right)^2 + y^2}} + \frac{-Q}{4 \pi ε \sqrt{ \left(d+x \right)^2 + y^2}} &= 0 \\ \\ 2\sqrt{ \left( d+x \right)^2 + y^2 } -\sqrt{ \left(2d-x \right)^2 + y^2 } &= 0 \\ \\ 2\sqrt{ \left( d+x \right)^2 + y^2} &= \sqrt{ \left( 2d-x \right)^2 + y^2 } \end{align} \)
ここで、両辺を2乗する。
\( \begin{align} 2^2 \times \left\{ \left( d+x \right)^2 + y^2 \right\} &= \left( 2d – x \right)^2 + y^2 \\ \\ 4\times \left( d^2 + 2dx + x^2 +y^2 \right) &= 4d^2 -8dx + x^2 + y^2 \\ \\ 3x^2 + 12dx +3y^2 &= 0 \\ \\ x^2 + 4dx +y^2 &= 0 \\ \\ x^2 +4dx +4d^2 -4d^2 +y^2 &= 0 \\ \\ (x+2d)^2 + y^2 -4d^2 &= 0 \\ \\ (x+2d)^2 + y^2 &= (2d)^2 \end{align} \)
この式は,円の公式
\( x^2 + y^2 = r^2 \)
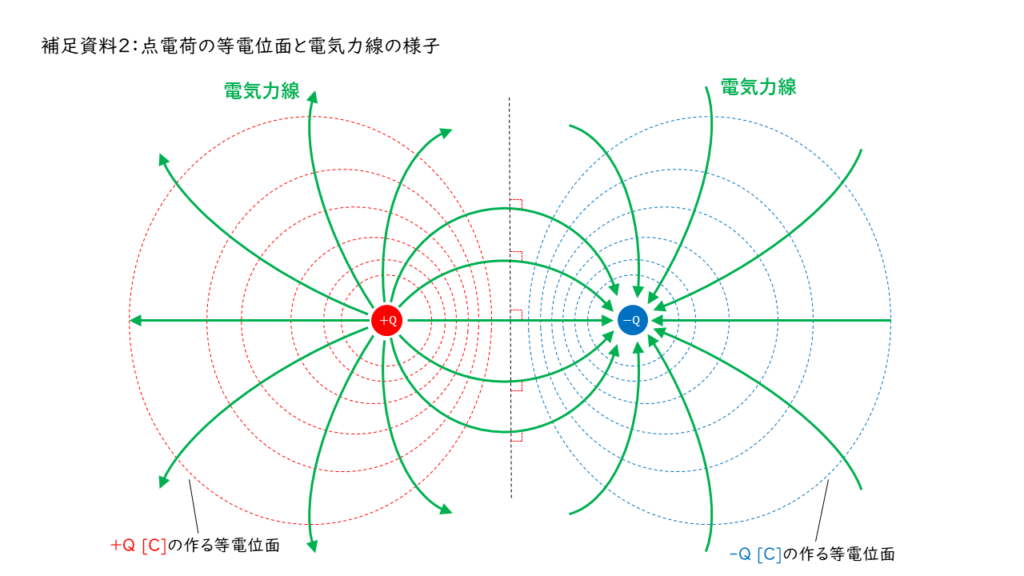
と同じ形の式であることから、電位が\(0\ V\)になる等電位線を表す図は中心\( (-2d,0) \)で,半径が\(2d\)の円となる。
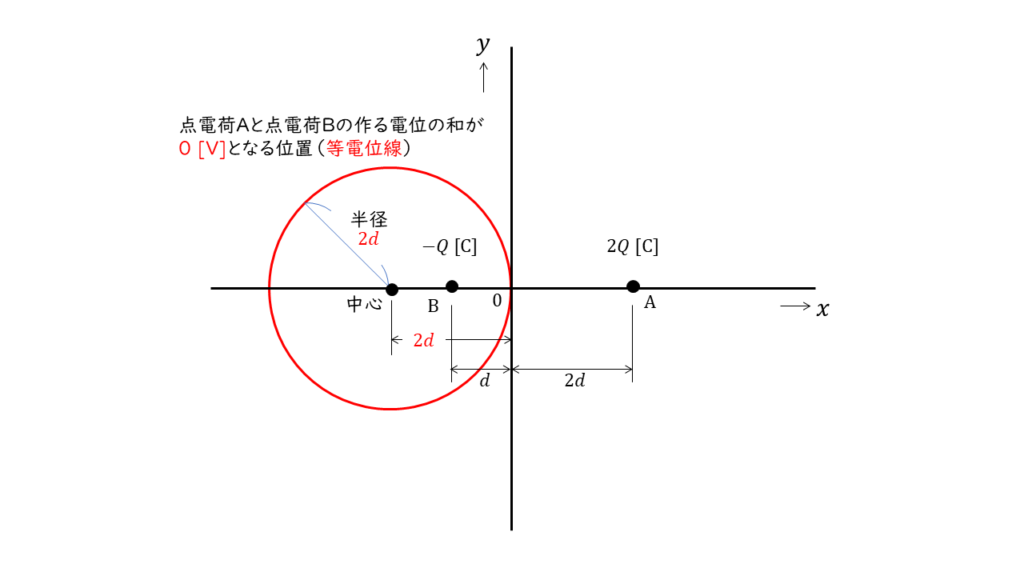
よって正解は(4)となる。
補足











コメント