問題
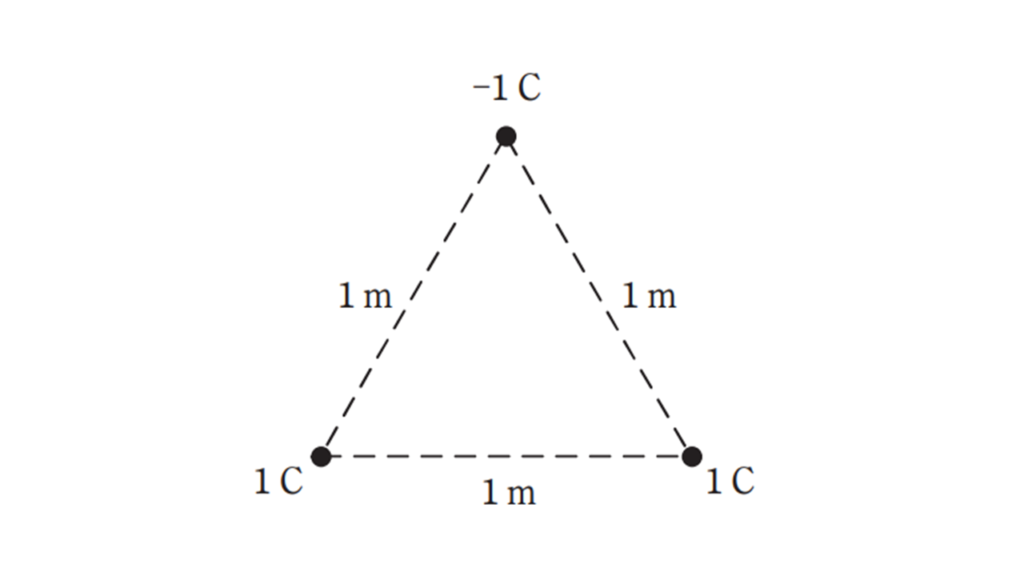
真空中において、図に示すように一辺の長さが \(1 \rm [m]\) の正三角形の各頂点に \( 1 \rm [C]\) 又は \(−1 \rm [C]\) の点電荷がある。この場合、正の点電荷に働く力の大きさ\( F_1 \rm [N]\) と、負の点電荷に働く力の大きさ\( F_2 \rm [N]\) の比 \(F_2 / F_1 \) の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
解説
答え:(3)
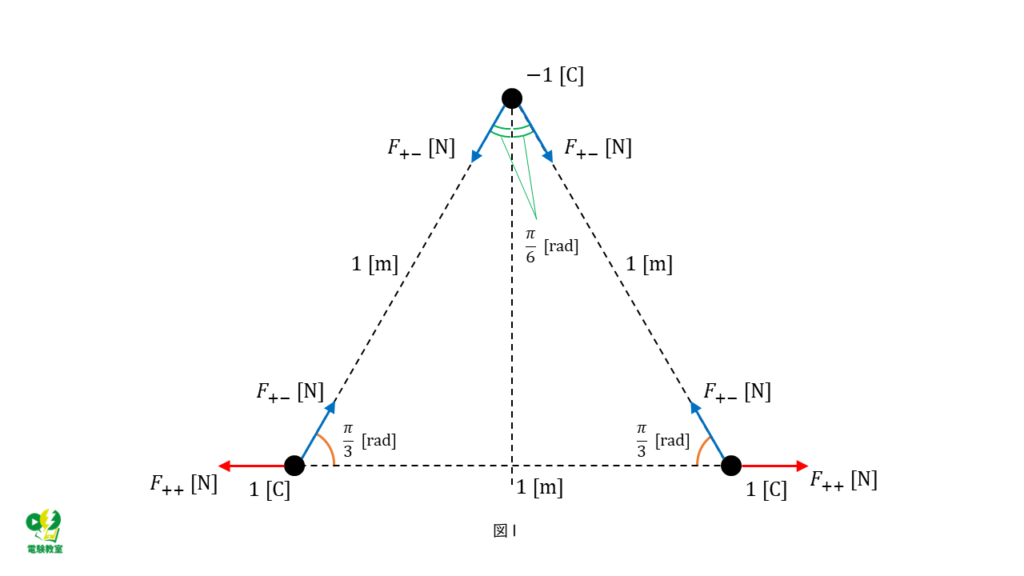
プラス同士の電荷の間にはたらく力を\(F_{++}\)、プラスとマイナスの電荷の間にはたらく力を\(F_{+-}\)で表すことにします。
それぞれの力の大きさは、真空中の誘電率を\(ε_0\)とすると、問題文で与えられた条件から以下のように表すことができます。
\( F_{++} = \displaystyle \frac{1 \times 1}{4 \pi ε _0 \times 1^2} = \displaystyle \frac{1}{4 \pi ε _0 }\)
\( F_{+-} = \displaystyle \frac{1 \times \left(-1\right) }{4 \pi ε _0 \times 1^2} = – \displaystyle \frac{1}{4 \pi ε _0 }\)
問で与えられた図に書き加えると図1のようになります。
正の点電荷に働く力の大きさ\( F_1 \) [N]を求める
正の点電荷に働く力のベクトルは、以下の図2のようになっています。
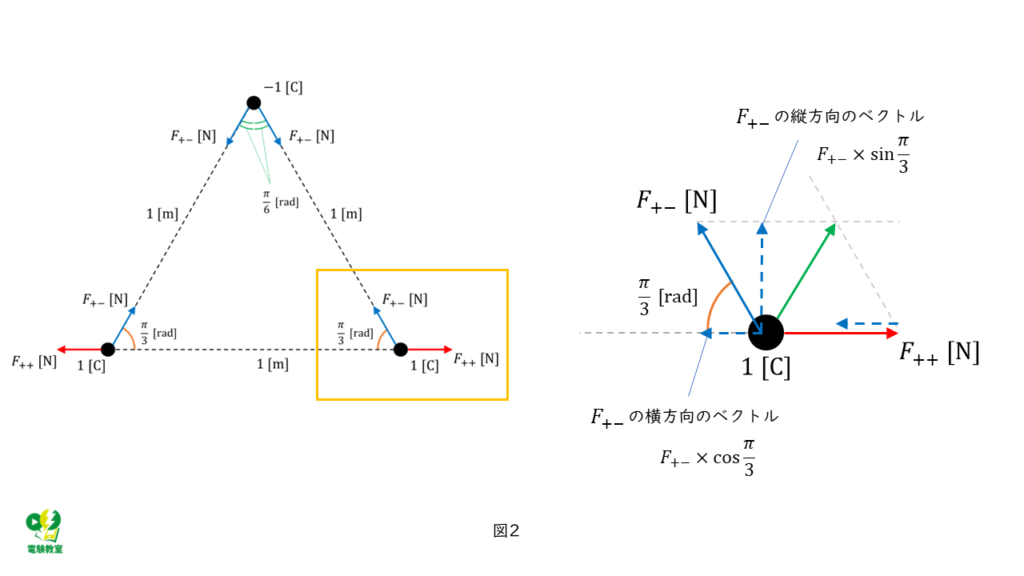
横方向のベクトルの合計は、
\( \begin{align} F &= \displaystyle \frac{1}{4 \pi ε _0 } + \left( – \displaystyle \frac{1}{4 \pi ε _0 } \times \cos \frac{\pi}{3} \right) \\ \\ &= \displaystyle \frac{1}{4 \pi ε _0 } + \left( – \displaystyle \frac{1}{4 \pi ε _0 } \times \frac{1}{2} \right) \\ \\ &= \displaystyle \frac{1}{8 \pi ε _0 } \end{align} \)
縦方向のベクトルの合計は、
\( \begin{align} F &= \displaystyle \frac{1}{4 \pi ε_0} \times \sin \frac{\pi}{3} \\ \\ &= \displaystyle \frac{1}{4 \pi ε_0} \times \frac{ \sqrt{3} }{2} \\ \\ &= \displaystyle \frac{ \sqrt{3} }{8 \pi ε_0} \end{align} \)
よって、ベクトル\(F_1\)[N]の大きさは、
\( \begin{align} F_1 &= \sqrt{ \left( \displaystyle \frac{1}{8 \pi ε _0 } \right)^2 + \left( \displaystyle \frac{ \sqrt{3} }{8 \pi ε _0 } \right)^2 } \\ \\ &= \sqrt{ \displaystyle \frac{2^2}{ \left( 8 \pi ε _0 \right)^2 } } \\ \\ &= \displaystyle \frac{2}{8 \pi ε _0 } = \displaystyle \frac{1}{4 \pi ε _0 } \end{align} \)
負の点電荷に働く力の大きさ\( F_2 \) [N]を求める
負の点電荷に働く力のベクトルは、以下の図3のようになっています。
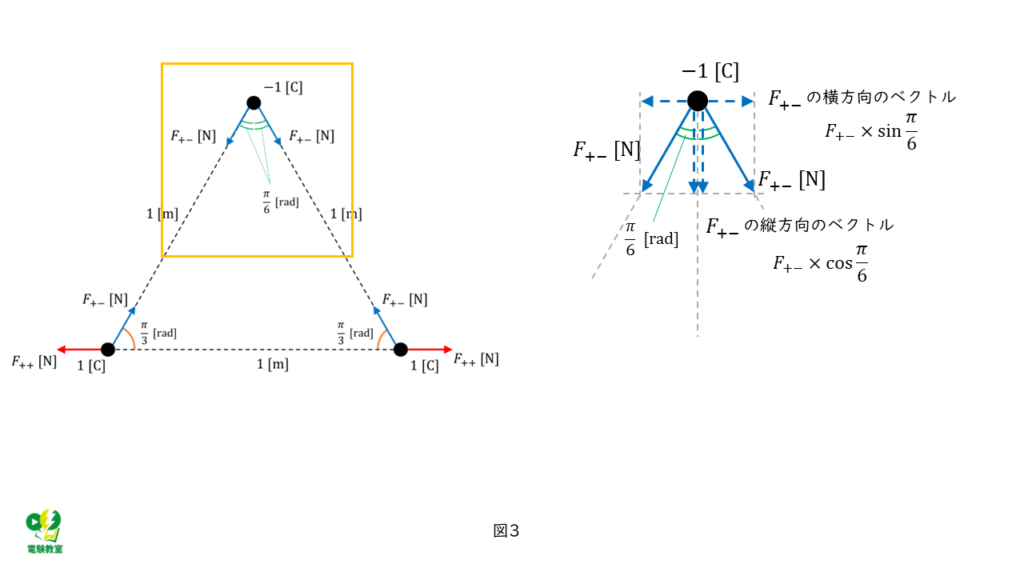
図3より、横方向のベクトルは左右に逆向きで、同じ大きさのベクトルであるため、0となる。
縦方向のベクトルの大きさは、
\( \begin{align} F &= \displaystyle \frac{1}{4 \pi ε _0 } \times \cos \frac{\pi}{6} + \displaystyle \frac{1}{4 \pi ε _0 } \times \cos \frac{\pi}{6} \\ \\ &= 2 \times \displaystyle \frac{1}{4 \pi ε _0} \times \frac{ \sqrt{3} }{2} \\ \\ &= \displaystyle \frac{ \sqrt{3} }{4 \pi ε _0} \end{align} \)
よってベクトル\(F_2\)[N]の大きさは、
\( \begin{align} F_2 &= \sqrt{ 0^2 + \left( \displaystyle \frac{ \sqrt{3} }{4 \pi ε _0} \right) ^2 } \\ \\ &= \displaystyle \frac{ \sqrt{3} }{4 \pi ε _0} \end{align} \)
点電荷にはたらく力の大きさの比\(F_2 / F_1 \)を求める
\( \displaystyle \frac{F_2}{F_1} = \displaystyle \frac{ \displaystyle \frac{1}{4 \pi ε _0 } }{ \displaystyle \frac{ \sqrt{3} }{4 \pi ε _0} } = \sqrt{3} \)
したがって、答えは(3)となる。











コメント