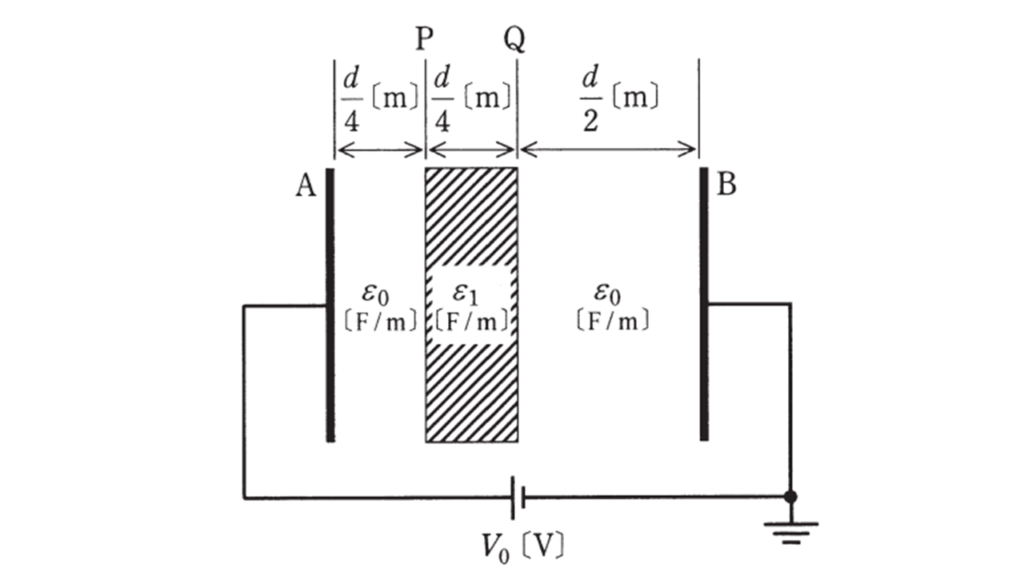
極板A-B間が誘電率\(ε_0\) [F/m]の空気で満たされている平行平板コンデンサのギャップ長を\(d\) [m],静電容量を\(C_0\) [F]とし,極板間の直流電圧を\(V_0\) [V]とする。極板と同じ形状の面積を持ち,厚さが\(\displaystyle \frac{d}{4}\) [m],誘電率\(ε_1\) [F/m]の個体誘電体\(ε_1 > ε_0\)を図に示す位置P-Q間に極板と平行に挿入すると,コンデンサ内の電位分布は変化し,静電容量は\(C_1\) [F]に変化した。このとき,誤っているものを次の(1)~(5)のうちから一つ選べ。
ただし,空気の誘電率を\(\varepsilon_0\),コンデンサの端効果は無視できるものとし,直流電圧\(V_0\) [V]は一定とする。
(1) 位置 P の電位は,固体誘電体を挿入する前の値よりも低下する。
(2) 位置 Q の電位は,固体誘電体を挿入する前の値よりも上昇する。
(3) 静電容量 \(C_1\) [F] は, \(C_0\) [F] よりも大きくなる。
(4) 固体誘電体を導体に変えた場合,位置 P の電位は固体誘電体又は導体を
挿入する前の値よりも上昇する。
(5) 固体誘電体を導体に変えた場合の静電容量 \(C_2\) [F] は, \(C_0\) [F] よりも大きくなる。
解説
答え:(4)
(1) 固体誘電体の挿入前後の位置 P の電位について
固体誘電体挿入前の電位について
直流電源に接続されたコンデンサ内の電位 \(V\) [V]と電界\(E\) [V/m],極板間距離 \(d\) [m]の間には以下のような関係が成り立ちます。
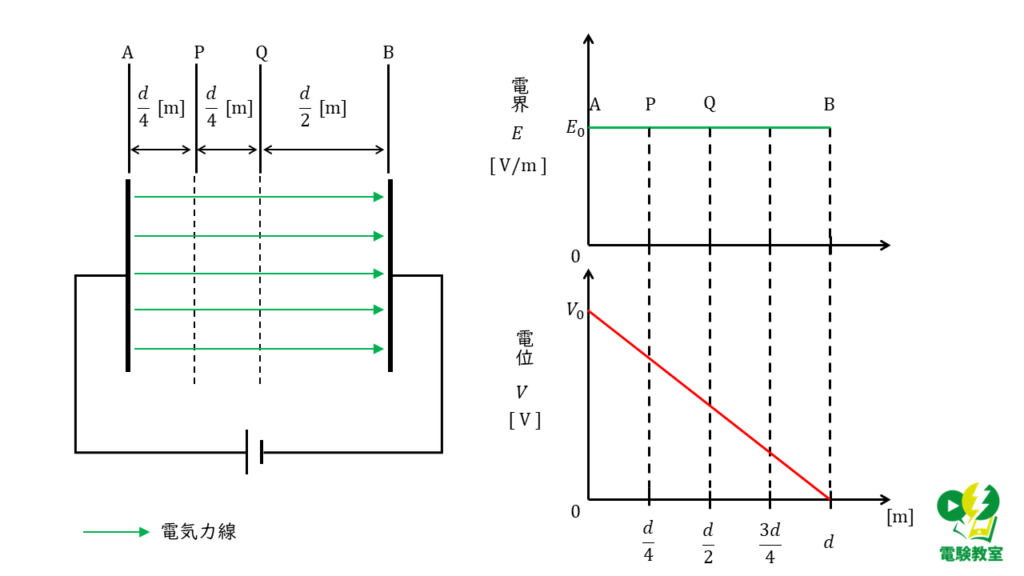
固体誘電体を挿入する前のコンデンサ内部の電界\(E\) [V/m]は,
\( E = \displaystyle \frac{V_0}{d} \)
となるので,電位の傾きは下図2のように表すことができます。
固体誘電体挿入後の電位について
誘電率 \(\varepsilon_1\) の固体誘電体を挿入したときの電束密度を\(D\)で表すると,空気部分の電界 \(E_0\) と誘電体部分の電界 \(E_1\) はそれぞれ次のように表すことができます。
\( E_0 = \displaystyle \frac{D}{\varepsilon_0} \)
\( E_1 = \displaystyle \frac{D}{\varepsilon_1} \)
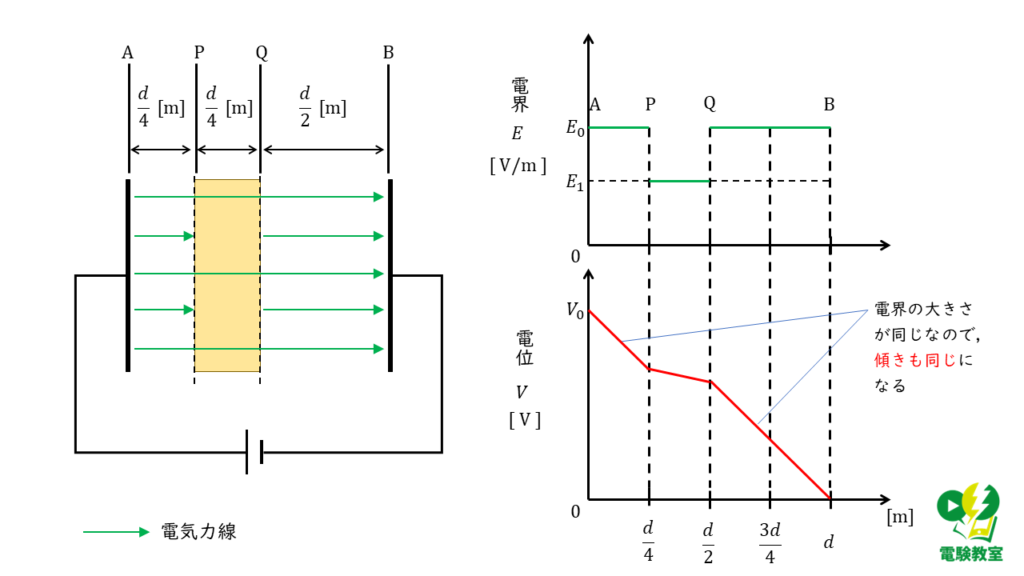
問題文の条件より,\( \varepsilon_1 > \varepsilon_0 \) なので,電界の大きさは, \( E_0 > E_1 \)となります。
よって,電界と電位は下図3のように表すことができます。
固体誘電体挿入前後での電位を比較する
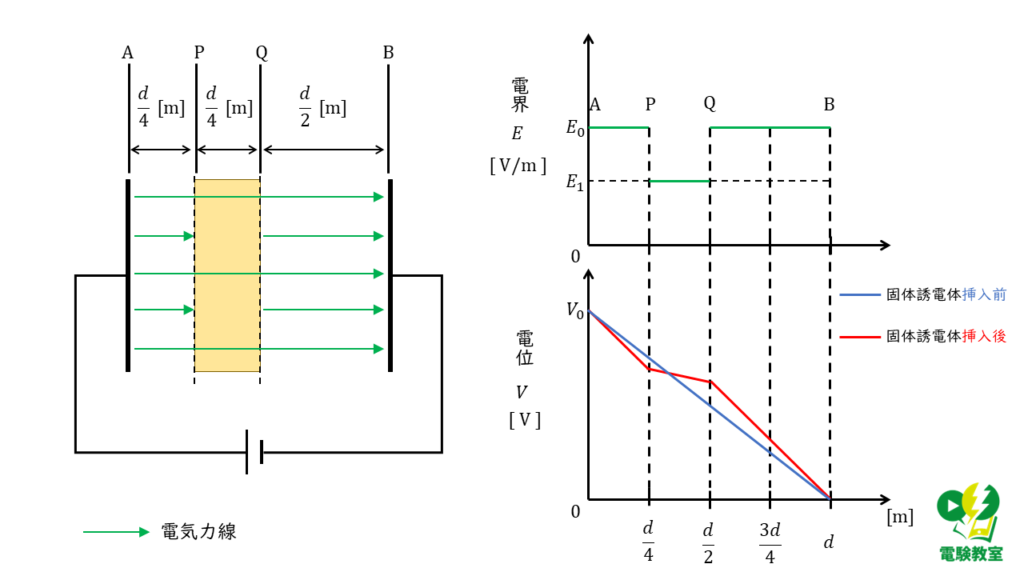
図2,図3の電位のグラフを重ね合わせると(図4),位置 P では,挿入前よりも電位が低くなっていることが分かります。
したがって,(1)は正しいことが分かります。
(2) 固体誘電体の挿入前後の位置 Q の電位について
(1)で求めた図4より,位置 Q では,挿入前よりも電位が高くなっていることが分かります。
したがって,(2)も正しいことが分かります。
(3) 固体誘電体挿入前後の静電容量について
極板の面積を \(S\) [\( \rm m^2\)]で表すとすると,個体誘電体挿入前の静電容量\(C_0\) [F]は,
\( C_0 = \varepsilon_0 \displaystyle \frac{S}{d} \)
で表すことができます。
静電容量 \( C_0\) と固体誘電体を挿入した場合の静電容量 \( C_1\) [F]との大小を比較するために,コンデンサ内部を全て固体誘電体で満たした場合の静電容量\( C_f \)について考えると,
\( C_f = \varepsilon_1 \displaystyle \frac{S}{d} \)
で表すことができ,誘電率は,\( \varepsilon_1 > \varepsilon_0 \) の関係にあることから静電容量は,
¥(C_f > C_0 \)
となります。よって問題の条件では,固体誘電体を挿入すると,静電容量が大きくなることが分かるので,コンデンサ内部の \(\displaystyle \frac{1}{4}\) が誘電体で満たされた状態にある静電容量\( C_1 \) の方が静電容量\( C_0\)よりも大きくなることが分かります。
したがって,(3)も正しいことが分かります。
極板の面積を\( S\) [\( \rm m^2\)]で表すこととします。
固体誘電体を挿入する前の静電容量 \( C_0\) [F]は,
\( C_0 = \varepsilon_0 \displaystyle \frac{S}{d} \)
となります。
一方、固体誘電体を挿入した後のコンデンサは,下の図のように考えることができます。
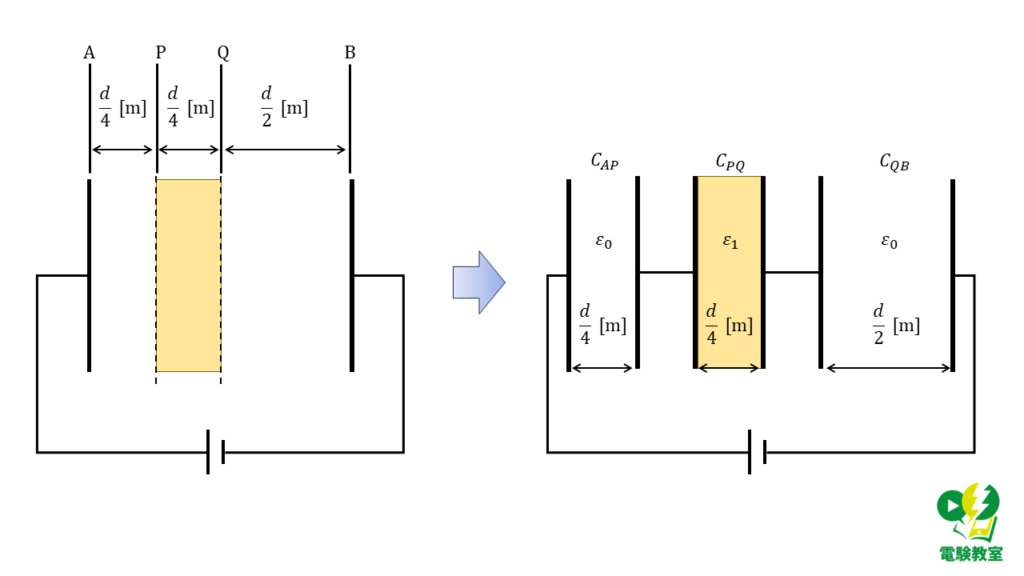
各位置までの静電容量は,それぞれ以下のように表すことができます。
\( C_AP = \varepsilon_0 \displaystyle \frac{S}{\displaystyle \frac{d}{4}} = \varepsilon_0 \displaystyle \frac{4S}{d} \)
\( C_PQ = \varepsilon_1 \displaystyle \frac{S}{\displaystyle \frac{d}{4}} = \varepsilon_1 \displaystyle \frac{4S}{d} \)
\( C_QB = \varepsilon_0 \displaystyle \frac{S}{\displaystyle \frac{d}{2}} = \varepsilon_0 \displaystyle \frac{2S}{d} \)
全体の合成容量 \( C_1 \) は,
\( \begin{align} \displaystyle \frac{1}{C_1} &= \displaystyle \frac{d}{4\varepsilon_0 S} + \displaystyle \frac{d}{4\varepsilon_1 S} + \displaystyle \frac{d}{2\varepsilon_0 S} \\ \\ &= \displaystyle \frac{\left( \varepsilon_1 d + \varepsilon_0 d + 2\varepsilon_1 d \right) }{4\varepsilon_0 \varepsilon_1 S} \\ \\ &=\displaystyle \frac{\left( 3\varepsilon_1 + \varepsilon_0 \right) d}{4\varepsilon_0 \varepsilon_1 S} \\ \\ C_1 &= \displaystyle \frac{4\varepsilon_1}{3\varepsilon_1 + \varepsilon_0} \times \displaystyle \frac{\varepsilon_0 S}{d} \end{align} \)
問題の条件より,\( \varepsilon_1 > \varepsilon_0\)であるから,
\( \displaystyle \frac{4\varepsilon_1}{3\varepsilon_1 + \varepsilon_0} > 1 \)
となるので,静電容量は ,\( C_1 > C_0 \)となります。
(4) 導体の挿入前後の位置 P の電位について
電気力線のルールより,導体内部には電気力線は存在しないので,導体内部の電界は0と考えることができます。
したがって、導体を挿入したときの電界と電位は図5のように表すことができます。

このとき,位置 P の電位は導体挿入前よりも低くなることがグラフから読み取れるので,(4)は誤りであることが分かります。
(5) 導体挿入前後の静電容量について
導体挿入後のコンデンサは図6のような回路と考えることができるので,この時の静電容量 \(C_2\) は,
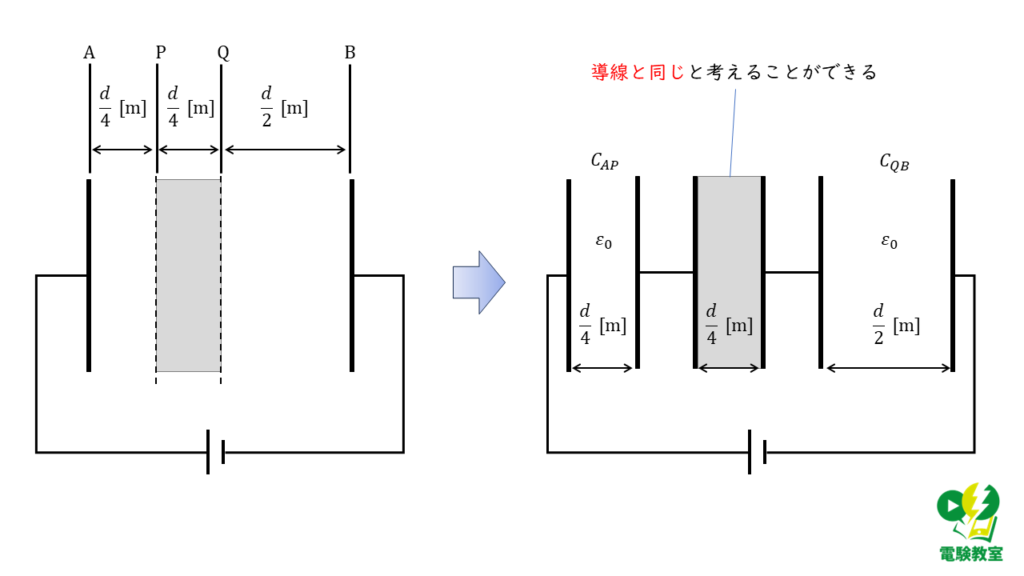
\( \begin{align} \displaystyle \frac{1}{C_2} = \displaystyle \frac{d}{4\varepsilon_0 S} + \displaystyle \frac{d}{2\varepsilon_0 S} \\ \\ &= \displaystyle \frac{3d}{4\varepsilon_0 S} \\ \\ C_2 &= \displaystyle \frac{4\varepsilon_0 S}{3d} \end{align} \)
よって導体挿入前の静電容量 \(C_0\) よりも \(C_2\) は,大きくなるので,(5)は正しいことが分かります。











コメント