問題
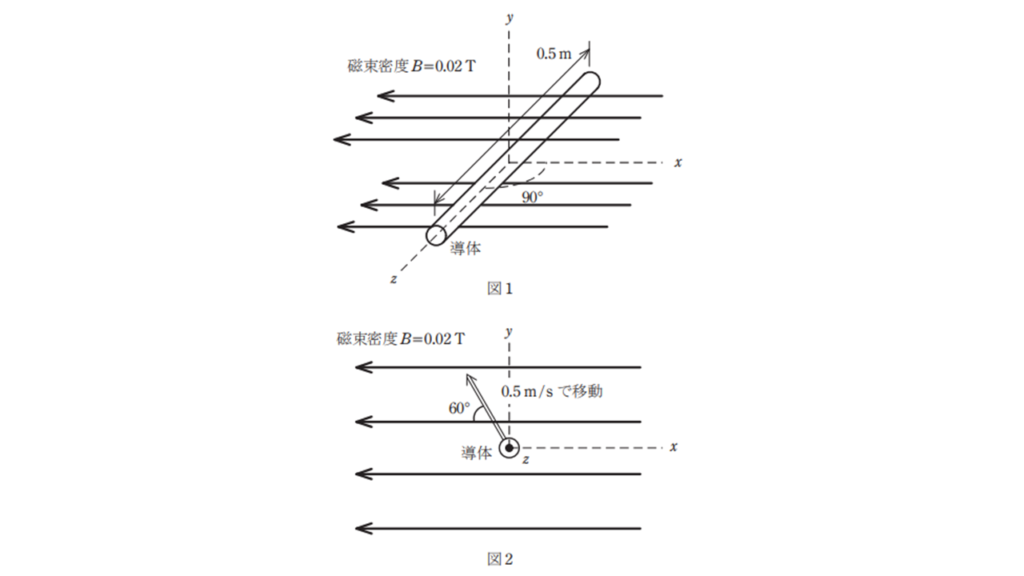
図1のように,磁束密度 \(B=0.02\ \rm T\) の一様な磁界の中に長さ \(0.5\ \rm m\) の直線状導体が磁界の方向と直角に置かれている。図2のようにこの導体が磁界と直角を維持しつつ磁界に対して \(60°\) の角度で,二重線の矢印の方向に \(0.5\ \rm m/s\) の速さで移動しているとき,導体に生じる誘導起電力 \(e\) の値 [\(\rm mV\)] として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,静止した座標系から見て,ローレンツ力による起電力が発生しているものとする。
(1) \(2.5\) (2) \(3.0\) (3) \(4.3\) (4) \(5.0\) (5) \(8.6\)
解説
答え:(3)
磁束に対して垂直に進む速度の大きさを求める
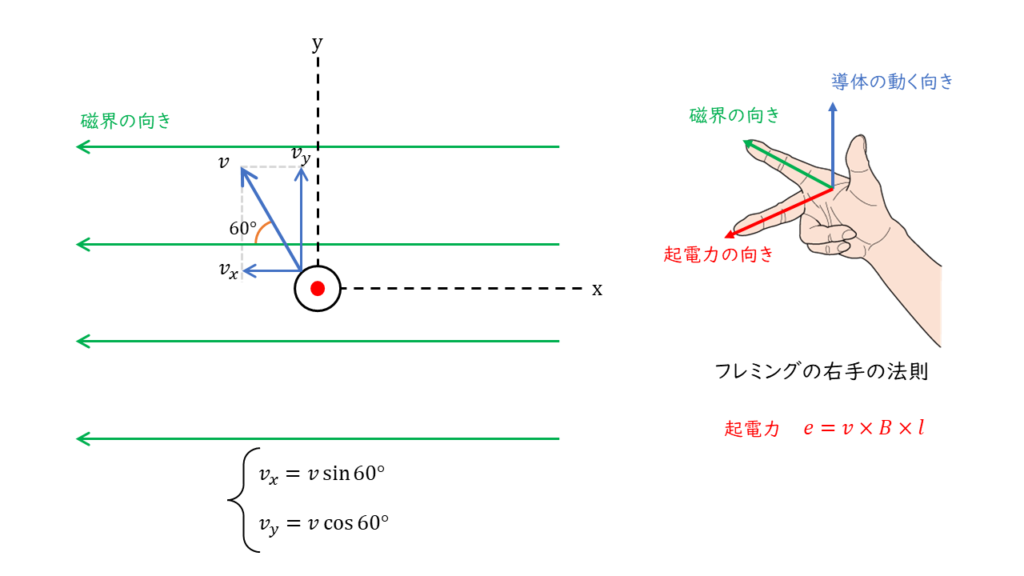
起電力は,フレミングの右手の法則より,磁界に対して,垂直に移動する導体に発生します。したがって,図から磁束に対して導体が垂直に移動する速度を求めます。
\( \begin{align} v_y &= v \times \cos 60^\circ \\ \\ &= 0.5 \times \displaystyle \frac{\sqrt{3}}{2} \\ \\ &= 0.25\sqrt{3} \end{align} \)
起電力を求める
起電力 \(e \ \rm [V]\) は,磁束密度\(B\ \rm [T] \),導体の長さ \(l \ \rm [m]\),磁束に垂直な移動速度 \(v_y \ \rm [m/s]\) より,
\( \begin{align} e &= v_y B l \\ &= 0.25\sqrt{3} \times 0.02 \times 0.5 \\ &= 4.33 \times 10^{-3} \ \rm [V] \end{align} \)
したがって,答えは(3)となります。











コメント