【過去問解説】R4下期理論　問5　抵抗のみの直流回路の計算問題

問題

図のような直流回路において，抵抗 \(3\ \Omega\) の端子間の電圧が \(1.8\ \rm V\) であった。このとき，電源電圧 \(E\ \rm [V]\) の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

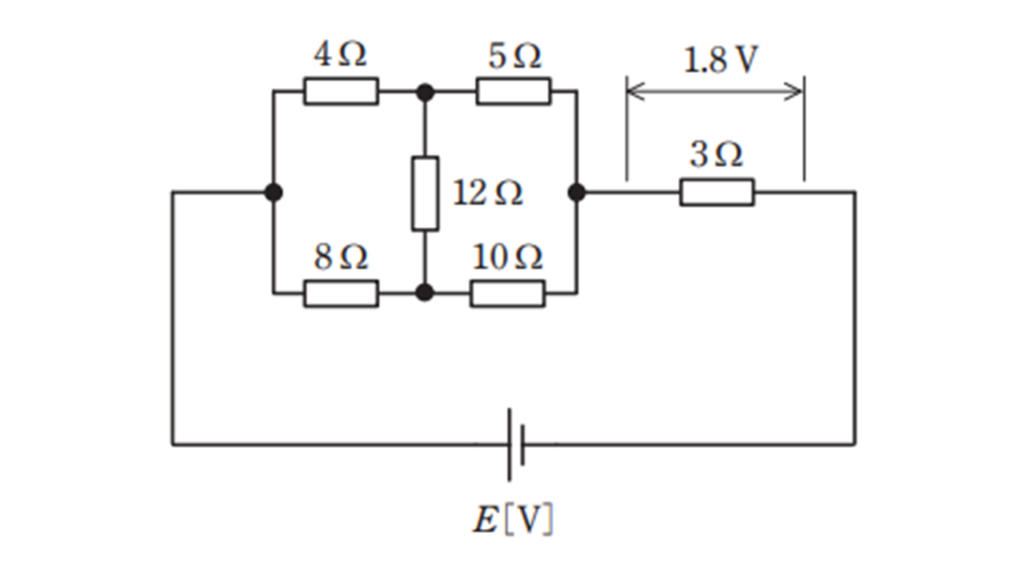
　(1)　 \(1.8\) 　(2)　 \(3.6\) 　(3)　 \(5.4\) 　(4)　 \(7.2\) 　(5)　 \(10.4\) 

解説

答え：（3）

ブリッジ回路の平衡条件を確認する

上図の赤枠の部分にブリッジ回路の平衡条件をあてはめると，

\( 4 \times 10 = 40 \tag{1} \)
\( 5 \times 8 = 40 \tag{2} \)

となり，式 (1)，(2) はどちらも \(40\ [\Omega]\) となるので，赤枠の部分のブリッジ回路は平衡条件を満たしていることが分かります。

したがって，中央の \(12\ [\Omega]\) の抵抗には電流は流れません。
そこで， \(12\ [\Omega]\) の抵抗は無いものとして回路を考えます。

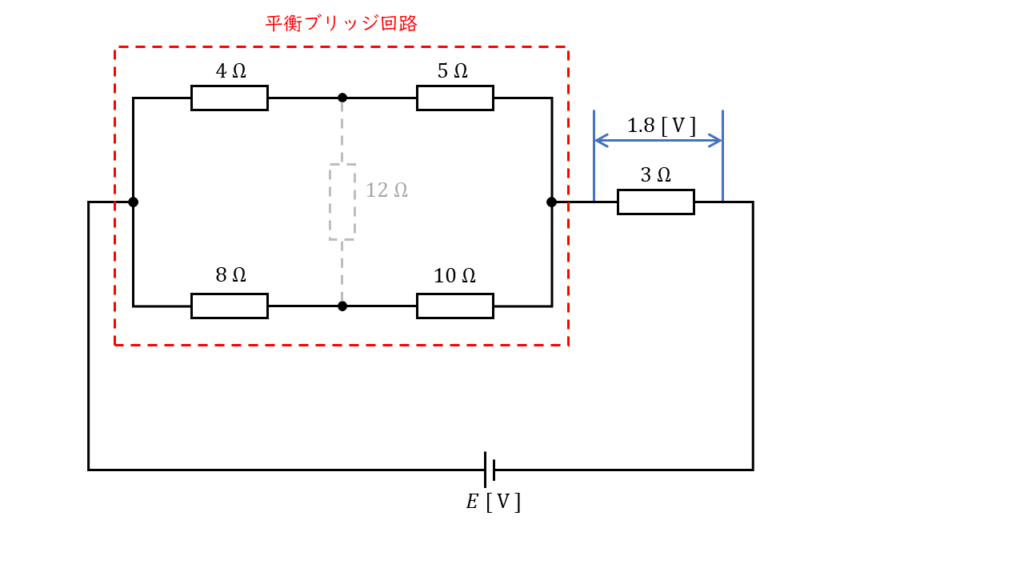
直流回路を計算し，電源電圧の大きさを求める

上図の赤枠の中をまとめると合計の抵抗の大きさは次のように計算できます。

\(\begin{align} R’ &= \displaystyle \frac{9 \times 18}{9+ 18} \\ \\ &= \displaystyle \frac{162}{27} \\ \\ &= 6 \ [\Omega] \end{align} \)

したがって，回路は下図のように書き換えることができます。

\(3\ [\Omega]\) の抵抗の両端にかかる電圧の大きさは \(1.8\ \rm [V]\) であるから，オームの法則より流れる電流 \(I\ \rm [A]\) の大きさは，

\( I = \displaystyle \frac{1.8}{3} = 0.6 \ \rm [A]\)

と計算できます。直列部分を流れる電流はどの点でも同じ大きさになるので， \(6\ [\Omega] \) の抵抗部分の両端にかかる電圧の大きさ \(V’\ \rm [V]\) は，

\( V’ = 0.6 \times 6 = 3.6 \ \rm [V]\)

となります。

直列回路の電源電圧の大きさは，各抵抗にかかる電圧の合計と等しくなるので，電源電圧 \(E\ \rm [V]\) の大きさは，

\( E = 3.6 + 1.8 = 5.4 \ \rm [V]\)

となるので，答えは(3)となります。