問題
図に示すように,面積が十分に広い平行平板電極(電極間距離 \(10 \ \rm[mm] \) )が空気(比誘電率 \(\varepsilon_{r1} = 1\) とする。)と,電極と同形同面積の厚さ \( 4\ \rm[mm]\) で比誘電率 \( \varepsilon_{r2} = 4\) の個体誘電体で構成されている。下部電極を接地し,上部電極に直流電圧 \(V\ \rm[kV]\) を加えた。次の(a)及び(b)に答えよ。
ただし,個体誘電体の導電性及び電極と個体誘電体の端効果は無視できるものとする。

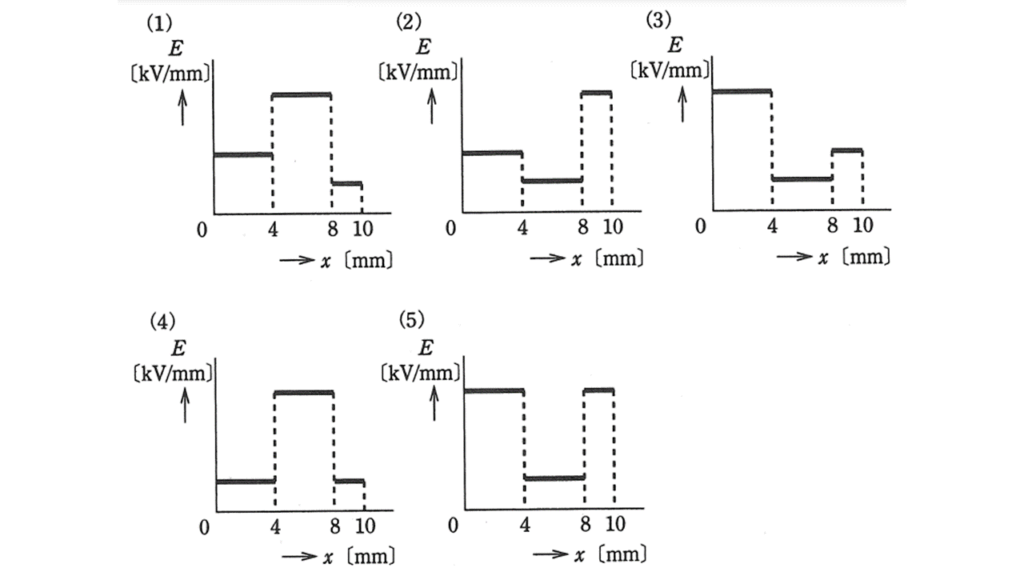
(a) 電極間の電界強さ \(E \ \rm[kV/m]\) のおおよその分布を示す図として,正しいのは次のうちどれか。
ただし,この時の電界の強さでは,放電は発生しないものとする。また,各図において,上部電極から下部電極に向かう距離を \(x \ \rm [mm]\) とする。
(b) 上部電極に加える電圧\(V \ \rm[kV]\) を徐々に増加し,下部電極側の空気中の電界の強さが \(2 \ \rm[kV/mm]\) に達したときの電圧 \(V \ \rm [kV]\) の値として,正しいのは次のうちのでれか。
(1) \(11\) (2) \(14\) (3) \(20\) (4) \(44\) (5) \(56\)
解説
答え:(a)-(5),(b)-(2)
(a) 電界の強さについて
直流電圧 \(V \ \rm[kV]\)を加えたときに蓄えられる電気量を \(Q\ \rm[C]\)と仮定します。
この時,電束密度を \(D \ \rm[C/mm^2]\) とすると,電界の強さ\( E \ \rm[kV/mm]\) は,
\( E = \displaystyle \frac{D}{\varepsilon} \)
の式で表すことができます。( \(\varepsilon\)は誘電率 [F/m]を表しています。 )
空気部分と個体誘電体部分で誘電率が異なるため,コンデンサ内部の電界の様子は下図のように考えることができます。
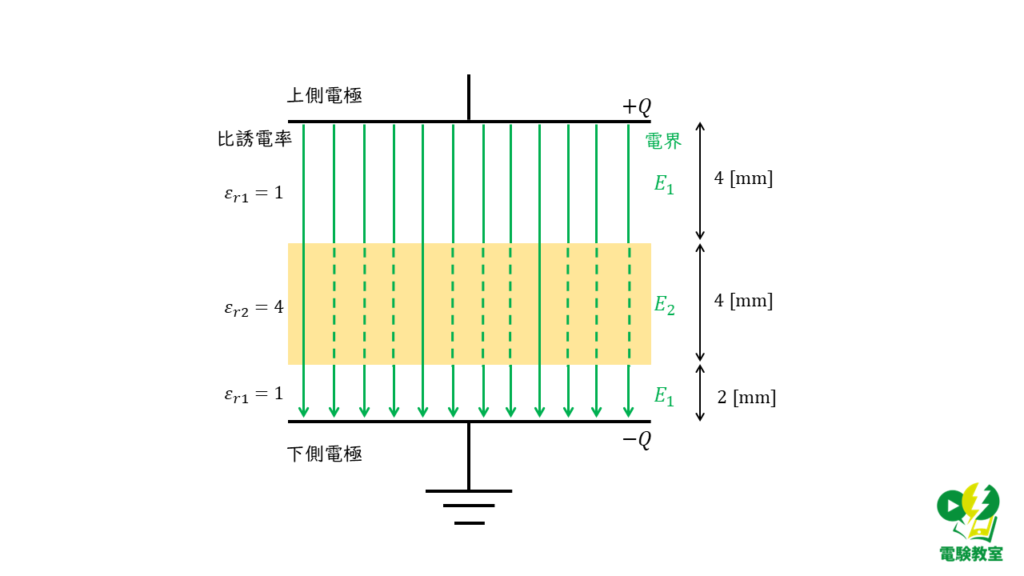
真空中の誘電率を \( \varepsilon_0 \)とすると,各部分の電荷の大きさは,
空気部分の電界の強さ
\( E_1 = \displaystyle \frac{D}{\varepsilon_0}\)
個体誘電体部分の電界の強さ
\( E_2 = \displaystyle \frac{D}{4\varepsilon_0} = \displaystyle \frac{E_1}{4} \)
したがって,(5)の図が正解となります。
(b) 下部電極側の電界の強さが\( 2\ \rm [kV/mm]\) となった時の電圧の大きさを求める
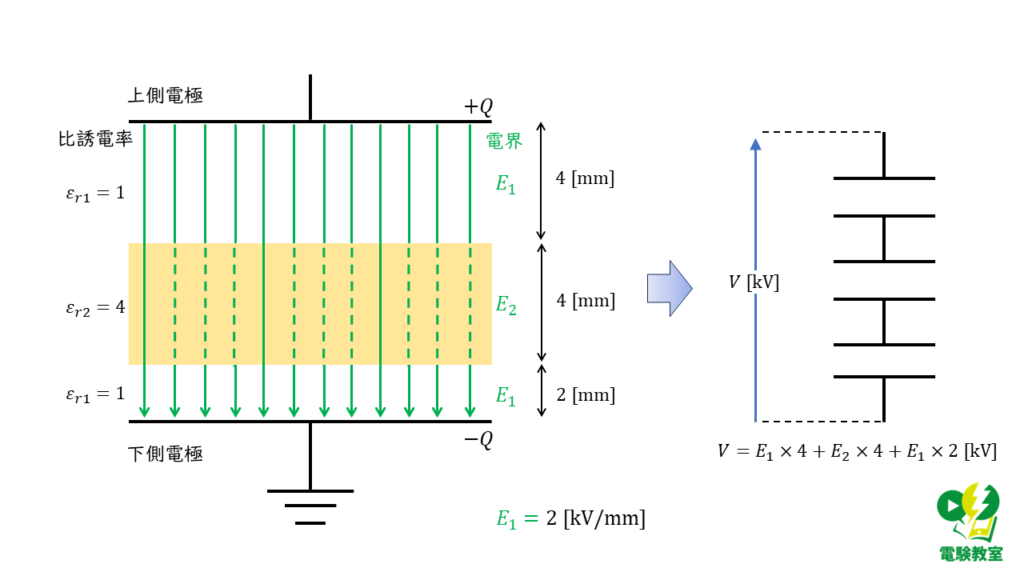
図より,3つのコンデンサが直列に接続されていると考えることができるので,\( V= E\times l\)より,電源電圧の大きさは,
\( V = \left( E_1 \times 4 \right) + \left( E_2 \times 4 \right) + \left( E_1 \times 2 \right) \ \rm[kV]\)
の式で求めることができます。
問題の条件より,\( E_1 = 2 \ \rm [kV/mm]\) ,(a)の答えより \(E_1 =4E_2\) であるから,
\( \begin{align} V &= \left( E_1 \times 4 \right) + \left( E_2 \times 4 \right) + \left( E_1 \times 2 \right) \\ \\ &= \left( 2\times 4 \right) + \left( \displaystyle \frac{2}{4} \times 4 \right) + \left( 2 \times 2 \right) =14 \ \rm[kV/mm] \end{align} \)
したがって,(2)が正解となります。











コメント