問題
静電気に関する記述として,正しいのは次のうちどれか。
(1) 二つの小さな帯電体の間に働く力の大きさは,それぞれの帯電体の電気量の和に比例し,
その距離の2乗に反比例する。
(2) 点電荷が作る電界は点電荷の電気量に比例し,距離に反比例する。
(3) 電気力線の任意の点での接線の方向は,その点の電界の方向に一致する。
(4) 等電位面上の正電荷には,その面に沿った方向に正のクーロン力が働く。
(5) コンデンサの電極板間にすき間なく誘電体を入れると,静電容量と電極板間の電界は,
誘電体の誘電率に比例して増大する。
解説
答え:(3)
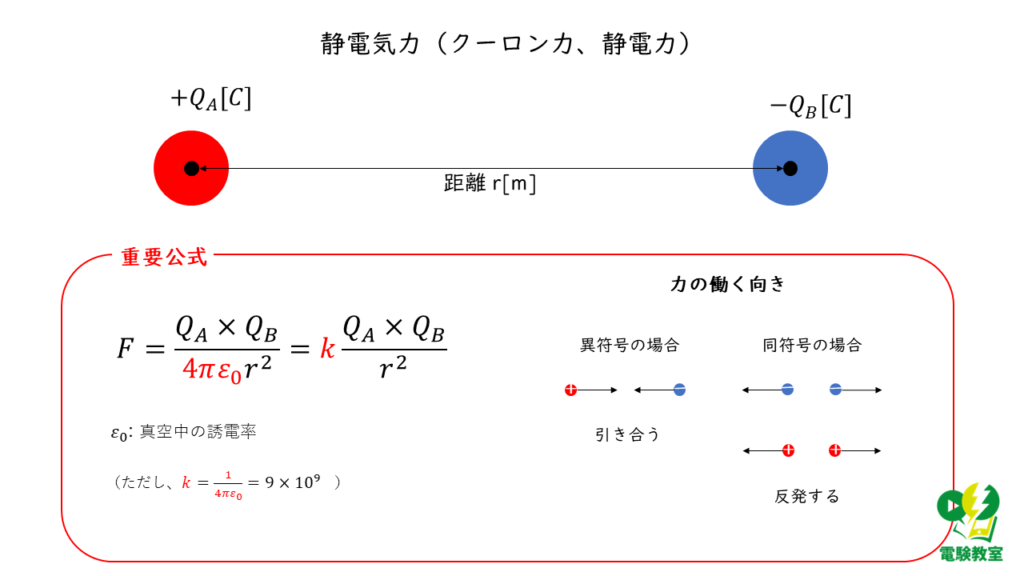
(1) 二つの帯電体間に働く静電気力について
帯電体A,Bがそれぞれ,電荷 \(Q_A \ \rm[C]\) ,\(Q_B \ \rm[C]\) で帯電し,帯電体間の距離が \(r \ \rm [m]\) であるとき,誘電率を \(\varepsilon\ \rm[F/m]\)とすると,静電気力 \(F\ \rm[N]\)は,
\( F = \displaystyle \frac{Q_A Q_B }{4 \pi \varepsilon r^2} \)
の式で表すことができます。
この式は,二つの電荷の積に比例し,距離の2乗に反比例することを表しているので,(1)は誤りとなります。
(2) 点電荷が作る電界について
点電荷 \(Q \ \rm[C]\) が作る電界 \(E \ \rm[V/m] \) は,誘電率を \(\varepsilon\ \rm[F/m]\) ,距離を \(r \ \rm[m] \) とすると次の式で表すことができます。
\( E = \displaystyle \frac{Q}{4 \pi \varepsilon r^2} \)
電界の大きさは,点電荷の電気量に比例し,距離の2乗に反比例するため,(2)も誤りとなります。
(3) 電気力線と電界の向きについて
電気力線の任意の点での接線は,その点における電界の向きを表しています。
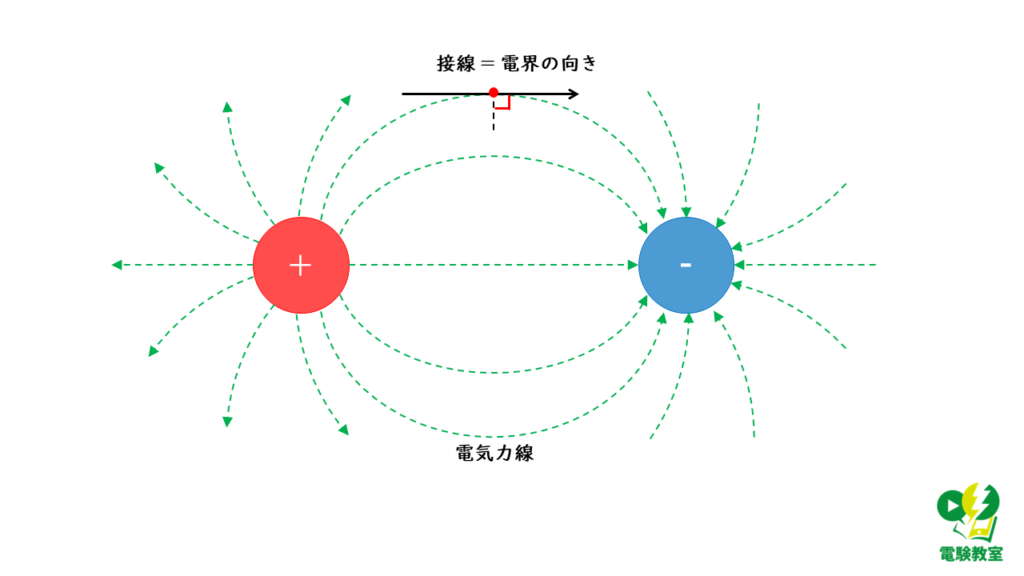
よって,(3)が正しいことが分かります。
(4) 等電位面について
等電位面は,電位の大きさが等しい地点を結んだとにできる面になります。
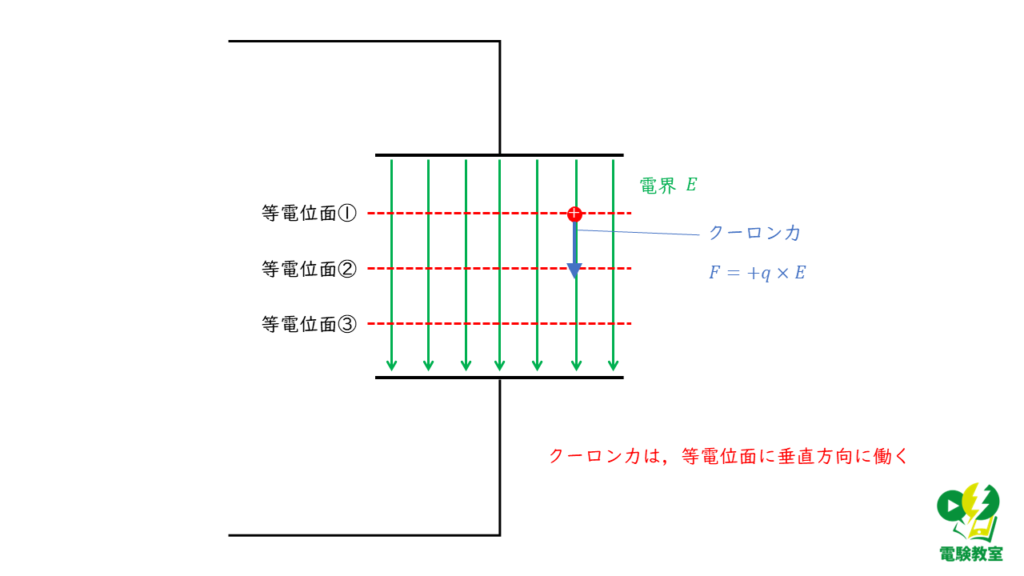
電荷にクーロン力を働かせる電界は,等電位面と垂直に交わるので,クーロン力が働く方向は,等電位面に対して垂直方向となります。
したがって,(4)も誤りとなります。
(5) コンデンサの静電容量,電界と誘電率の関係について
コンデンサの静電容量\(C \ \rm[F]\) は,電極板面積を \(S\ \rm[m^2]\) ,極板間距離を \(d \ \rm[m]\) ,誘電率を \(\varepsilon \ \rm [F/m]\)とすると,
\( C = \varepsilon \displaystyle \frac{S}{d} \)
と表すことができ,誘電率に比例することが分かります。
一方,コンデンサの電界 \( E \ \rm[V/m\) は,電源電圧を \(V \ \rm[V]\)とすると,
\( E = \displaystyle \frac{V}{d} \)
で表され,誘電率に依存しないため,(5)も誤りであることが分かります。











コメント