問題
図のように,点 \(\rm O\) を中心とするそれぞれ半径 \(1\ \rm[m]\) と半径 \(2\ \rm[m]\) の円形導線の \(\displaystyle \frac{1}{4}\) とそれらを連結する直線状の導線からなる扇形導線がある。この導線に,図に示す向きに直流電流 \(I = 8\ \rm[A]\) を流した場合,点 \(\rm O\) における磁界 \(\rm [A/m]\) の大きさとして,正しいのは次のうちどれか。
ただし,扇形導線は同一平面上にあり,その巻数は一巻きである。
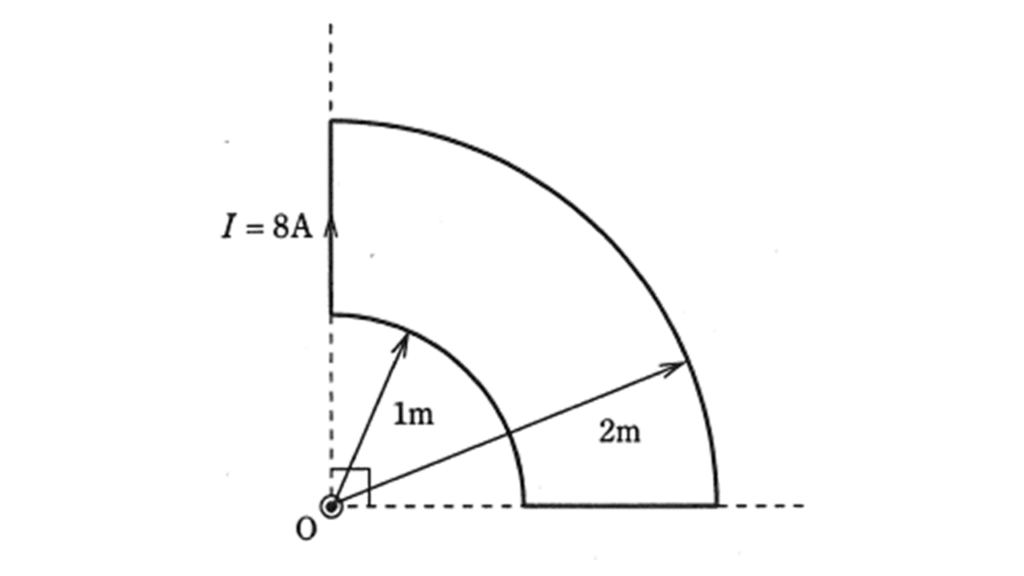
(1) \(0.25\) (2) \(0.5\) (3) \(0.75\) (4) \(1.0\) (5) \(2.0\)
解説
答え:(2)
半径 \(1\ \rm m\) の円形導体が作る磁界の大きさ
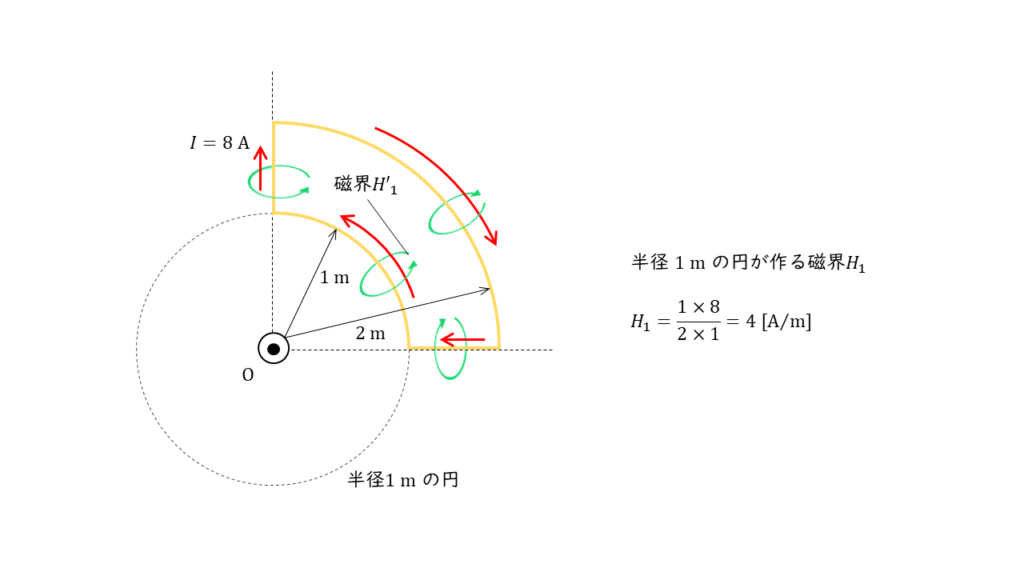
問の図より,半径 \(1\ \rm m\) の円形導体に流れる電流は上図のようになるので,「ビオ・バザールの法則」より円形導体の作る磁界 \(H_1\) の大きさは,
\(\begin{align} 磁界 &= \displaystyle \frac{巻数 \times 電流}{2 \times 半径} \\ \\ H_1 &= \displaystyle \frac{1 \times 8}{2 \times 1} \\ \\ &= 4 \ \rm [A/m] \end{align} \)
と計算することができます。問題の図では,円形導体の \(\displaystyle \frac{1}{4}\) の扇型しか書かれていないため,発生する磁界の大きさも \(\displaystyle \frac{1}{4}\) になります。
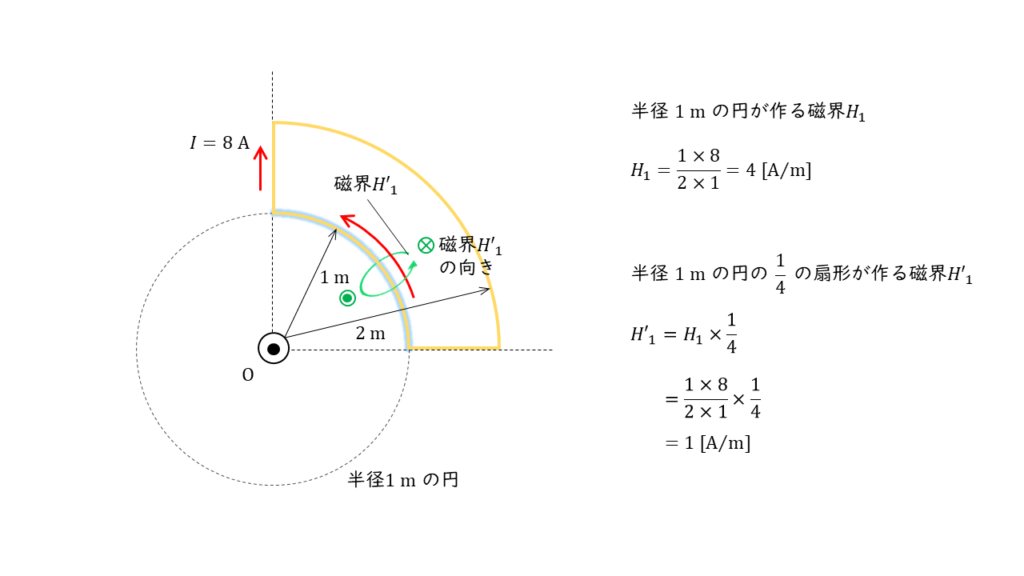
したがって,半径 \(1\ \rm m\) の扇形の作る磁界の大きさ \(H’_1\) は,
\(\begin{align} H’_1 &= H_1 \times \displaystyle \frac{1}{4} \\ \\ &= 4 \times \displaystyle \frac{1}{4} \\ &= 1\ \rm[A/m] \end{align} \)
となります。
半径 \(2\ \rm m\) の円形導体が作る磁界の大きさ
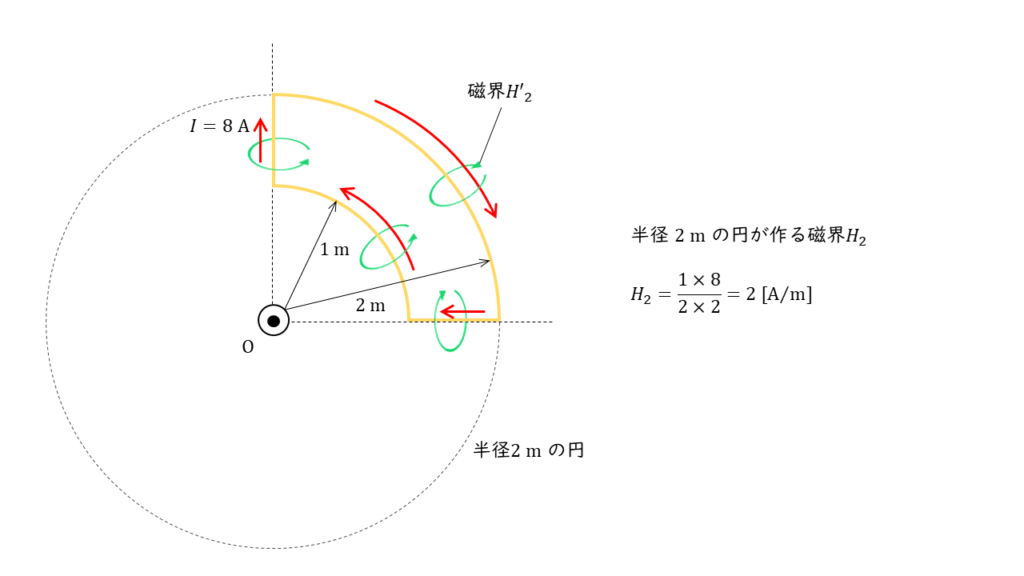
問の図より,半径 \(2\ \rm m\) の円形導体に流れる電流は上図のようになるので,「ビオ・バザールの法則」より円形導体の作る磁界 \(H_2\) の大きさは,
\(\begin{align} 磁界 &= \displaystyle \frac{巻数 \times 電流}{2 \times 半径} \\ \\ H_2 &= \displaystyle \frac{1 \times 8}{2 \times 2} \\ \\ &= 2 \ \rm [A/m] \end{align} \)
と計算することができます。問題の図では,円形導体の \(\displaystyle \frac{1}{4}\) の扇型しか書かれていないため,発生する磁界の大きさも \(\displaystyle \frac{1}{4}\) になります。
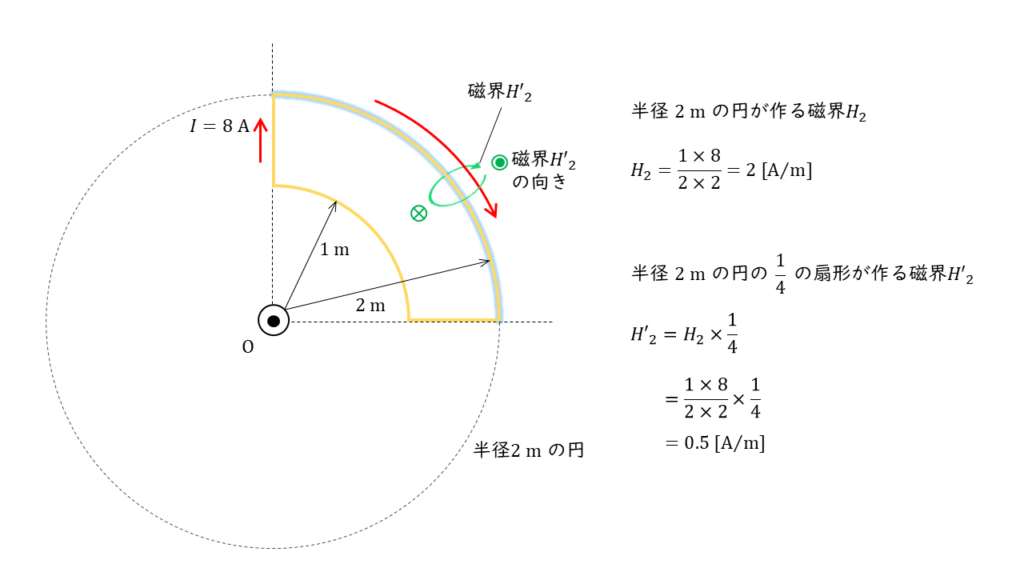
したがって,半径 \(1\ \rm m\) の扇形の作る磁界の大きさ \(H’_1\) は,
\(\begin{align} H’_2 &= H_2 \times \displaystyle \frac{1}{4} \\ \\ &= 2 \times \displaystyle \frac{1}{4} \\ &= 0.5 \ \rm [A/m] \end{align} \)
となります。
発生する磁界の合計の大きさを求める
半径 \(1\ \rm m\) の扇型導体,半径 \(2\ \rm m\) の扇型導体の作る磁界の向きは下図のようになり,それぞれ反対向きになっています。
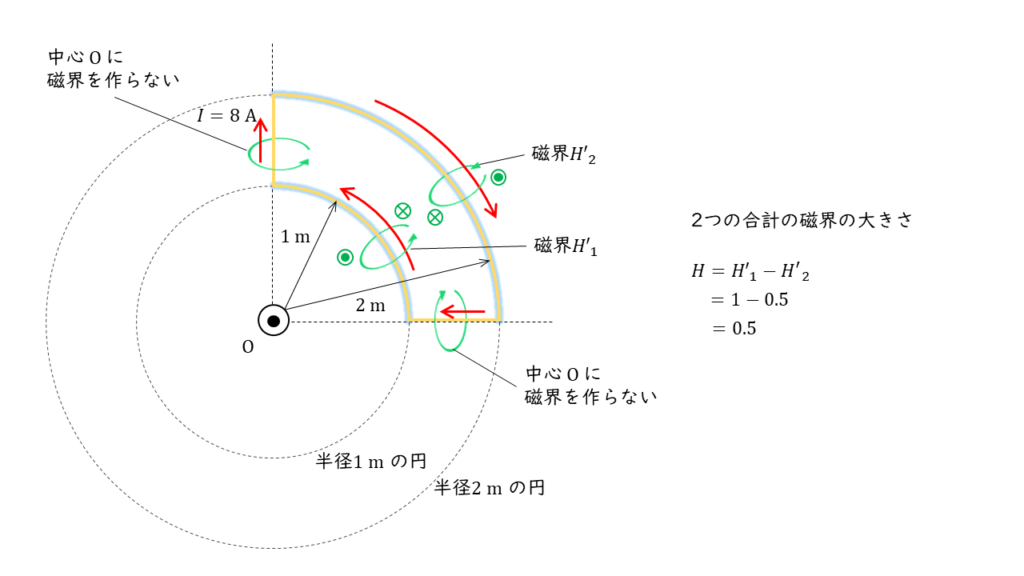
紙面に向かって上方向を正と考えると,合計の磁界の大きさ \(H\) は,
\(\begin{align} H &= H’_1 – H’_2 \\ &= 1 – 0.5 \\ &= 0.5 \end{align} \)
となり,答えは(2)と求まります。











コメント