問題
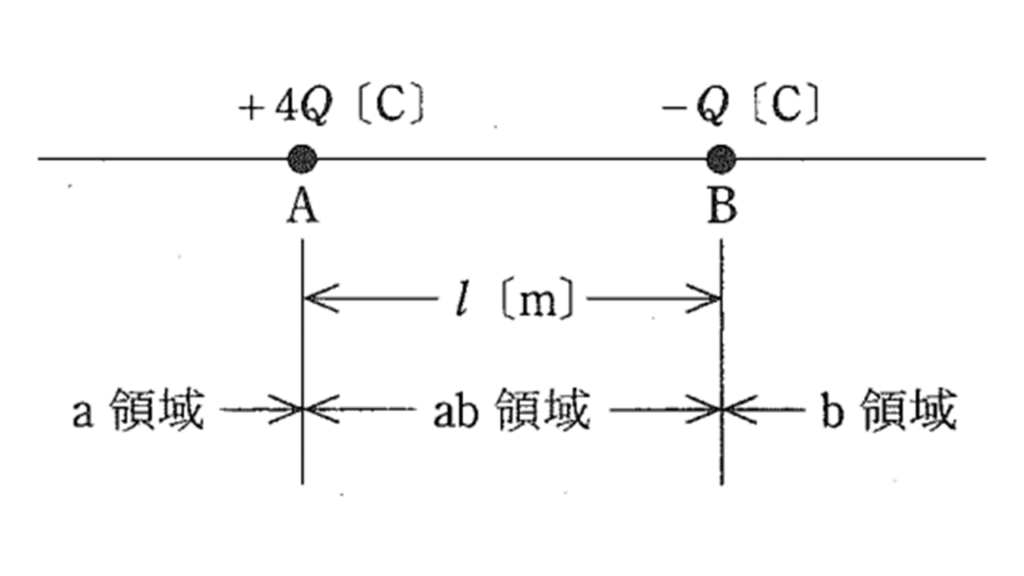
真空中において,図のように点 A に正電荷 \(+4Q\) [C] ,点 B に負電荷 \(−Q\) [C] の点電荷が配置されている。この 2 点を通る直線上で電位が \(0\) [V] になる点を点 P とする。点 P の位置を示すものとして,正しいものを組み合わせたのは次のうちどれか。なお,無限遠の点は除く。
ただし,点 A と点 B 間の距離を l [m] とする。また,点 A より左側の領域を a 領域,点 A と点 B の間の領域を ab 領域,点 B より右側の領域を b 領域とし,真空の誘電率を \(\varepsilon_0\) [F/m] とする。
$$ \begin{array}{cccc} \ & a領域 & ab領域 & b領域 \\ \hline (1) &点 A より左 \displaystyle \frac{l}{3}\ [\rm m] の点 &この領域には存在しない &点 B より右 l\ [\rm m] の点 \rule[-5mm]{0mm}{15mm} \\ \hline (2) &この領域には存在しない &点 A より右 \displaystyle \frac{4l}{5}\ [\rm m] の点 &点 B より右 \displaystyle \frac{l}{3}\ [\rm m] の点 \rule[-5mm]{0mm}{15mm} \\ \hline (3) &この領域には存在しない &この領域には存在しない &点 B より右 l\ [\rm m] の点 \rule[-5mm]{0mm}{15mm} \\ \hline (4) &点 A より左 \displaystyle \frac{l}{3}\ [\rm m] の点 &点 A より右 \displaystyle \frac{4l}{5}\ [\rm m] の点 &点 B より右 \displaystyle \frac{l}{3}\ [\rm m] の点 \rule[-5mm]{0mm}{15mm} \\ \hline (5) &この領域には存在しない &点 A より右 \displaystyle \frac{4l}{5}\ [\rm m] の点 &点 B より右 l\ [\rm m] の点 \\ \hline \end{array} $$
解説
答え:(2)
a領域における電位を計算する
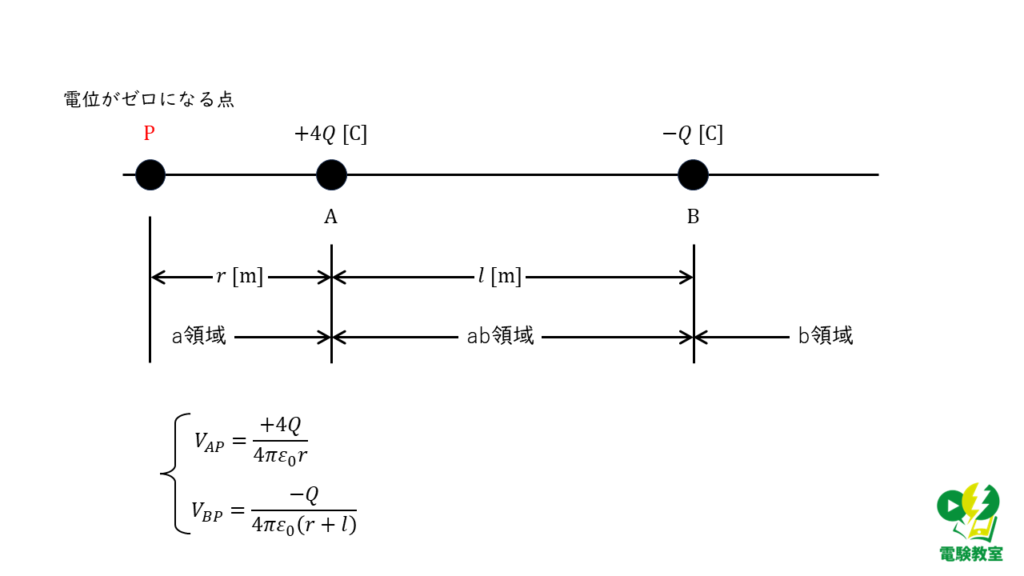
点Pから点Aまでの距離を\(r\) [m]とした場合,点Aの電荷による電位\( V_{AP}\)と点Bの電荷による電位\( V_{BP}\)はそれぞれ以下の式で表すことができます。
\( V_{AP} = \displaystyle \frac{+4Q}{4\pi \varepsilon_0 r} \) [V]
\( V_{BP} = \displaystyle \frac{-Q}{4\pi \varepsilon_0 \left( r + l \right) } \) [V]
ただし,\( r >0 \)
点Pでは電位が\(0\) [V]になるので,
\( \begin{align} V_{AP} + V_{BP} &= 0 \\ \\ \displaystyle \frac{+4Q}{4\pi \varepsilon_0 r} + \displaystyle \frac{-Q}{4\pi \varepsilon_0 \left( r + l \right) } &= 0 \\ \\ \displaystyle \frac{+4Q}{4\pi \varepsilon_0 r} &= \displaystyle \frac{Q}{4\pi \varepsilon_0 \left( r + l \right)} \\ \\ 4\times \left( r + l \right) &= r \\ \\ 3r &= -4l \\ \\ r &= -\displaystyle \frac{4l}{3} \end{align} \)
と計算することができますが,\( r = – \displaystyle \frac{4l}{3} < 0 \)となってしまうため,条件に当てはまりません。
したがって,a領域には,電位が\(0\) [V]となる位置が存在しないことが分かります。
ab領域における電位を計算する
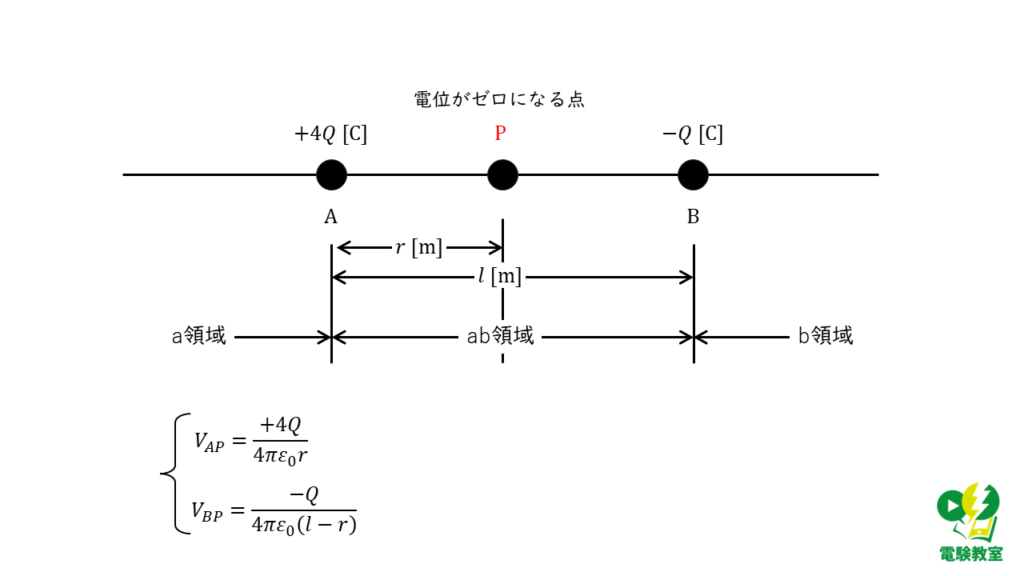
点Pから点Aまでの距離を\(r\) [m]とした場合,点Aの電荷による電位\( V_{AP}\)と点Bの電荷による電位\( V_{BP}\)はそれぞれ以下の式で表すことができます。
\( V_{AP} = \displaystyle \frac{+4Q}{4\pi \varepsilon_0 r} \) [V]
\( V_{BP} = \displaystyle \frac{-Q}{4\pi \varepsilon_0 \left( l – r l \right) } \) [V]
ただし,\( r >0 \)
点Pでは電位が\(0\) [V]になるので,
\( \begin{align} V_{AP} + V_{BP} &= 0 \\ \\ V_{AP} &= -V_{BP} \\ \\ \displaystyle \frac{+4Q}{4\pi \varepsilon_0 r} &= \displaystyle \frac{Q}{4\pi \varepsilon_0 \left( l – r l \right) } \\ \\ 4 \left( l – r \right) &= r \\ \\ 5r &= 4l \\ \\ r &= \displaystyle \frac{4l}{5} \end{align} \)
と計算することができます。\( r = \displaystyle \frac{4l}{5} > 0\)なので,条件に当てはまるため,ab領域で電位が\( 0\) [V]となるのは,点Aから右に\( \displaystyle \frac{4l}{5} \) [m]の位置となります。
b領域における電位を計算する
点Pから点Bまでの距離を\(r\) [m]とした場合,点Aの電荷による電位\( V_{AP}\)と点Bの電荷による電位\( V_{BP}\)はそれぞれ以下の式で表すことができます。
\( V_{AP} = \displaystyle \frac{+4Q}{4\pi \varepsilon_0 \left( r + l \right) } \) [V]
\( V_{BP} = \displaystyle \frac{-Q}{4\pi \varepsilon_0 r } \) [V]
ただし,\( r >0 \)

点Pでは電位が\(0\) [V]になるので,
\( \begin{align} V_{AP} + V_{BP} &= 0 \\ \\ V_{AP} &= -V_{BP} \\ \\ \displaystyle \frac{+4Q}{4\pi \varepsilon_0 \left( r + l \right) } &= \displaystyle \frac{Q}{4\pi \varepsilon_0 r } \\ \\ 4r &= \left( r + l \right) \\ \\ 3r &= l \\ \\ r &= \displaystyle \frac{l}{3} \end{align} \)
と計算することができます。\( r = \displaystyle \frac{l}{3} > 0\)なので,条件に当てはまるため,b領域で電位が\( 0\) [V]となるのは,点Bから右に\( \displaystyle \frac{l}{3} \) [m]の位置となります。
したがって,答えは(2)になります。











コメント