問題
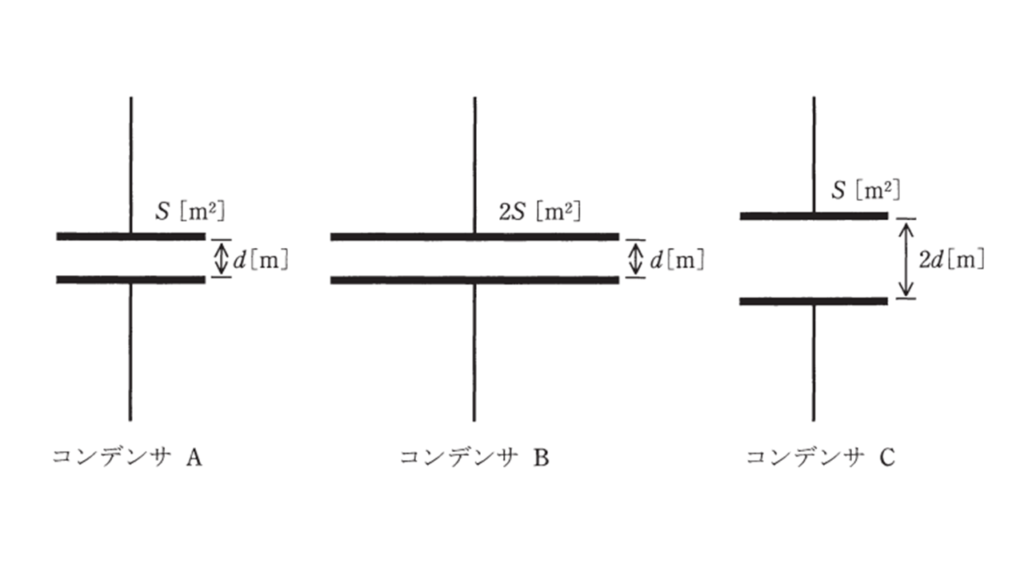
極板の面積\(S\ \rm[m^2]\),極板間の距離\(d\ \rm [m]\)の平行板コンデンサ\(A\),極板の面積\(2S\ \rm[m^2]\),極板間の距離\(d\ \rm [m] \)の平行板コンデンサ\(B\)及び極板の面積\(S\ \rm[m^2]\),極板間の距離\(2d\ [m]\)の平行板コンデンサ\(C\)がある。各コンデンサは,極板間の電界の強さが同じ値となるようにそれぞれ直流電源で充電されている。各コンデンサをそれぞれの直流電源から切り離した後,全コンデンサを同じ極性で並列に接続し,十分時間が経ったとき,各コンデンサに蓄えられる静電エネルギーの総和の値\(\ \rm[J]\)は、並列に接続する前の総和の値\(\ \rm[J]\)の何倍になるか。その倍率として,最も近いものを次に\((1)~(5)\)のうちから一つ選べ。
ただし,各コンデンサの極板間の誘電率は同一であり,端効果は無視できるものとする。
$$ (1)\ 0.77 \ \ \ \ (2)\ 0.91 \ \ \ \ (3)\ 1.00 \ \ \ \ (4)\ 1.09 \ \ \ \ (5)\ 1.31 $$
解説
答え:(2)
静電エネルギーの公式
$$ W = \displaystyle \frac{1}{2} C V^2 = \displaystyle \frac{1}{2} QV = \displaystyle \frac{1}{2} \displaystyle \frac{Q^2}{C} $$
を利用して問題を解いていく。
並列接続前の静電エネルギーの総和を求める
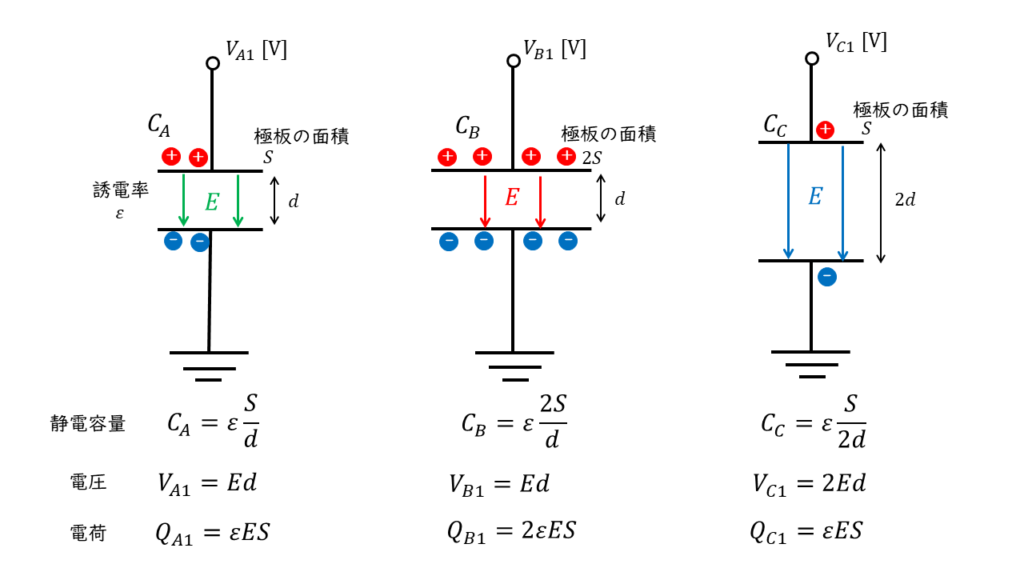
コンデンサA,B,C の各静電容量\(C_A,C_B,C_C \ \rm [F]\)は以下の様に計算できる。
\( C_A = \displaystyle ε \frac{S}{d} \\ C_B = \displaystyle ε \frac{2S}{d} \\ C_C = \displaystyle ε \frac{S}{2d} \)
問題文より,極板間に同じ大きさの電界が生じるように直流電源で充電されているので,各コンデンサの両端の電位差\(V\ \rm[V]\)は電界の大きさを\( E\ \rm[V/m]\)とすると,
\( V_{A1} = E \times d = Ed \\ V_{B1} = Ed \\ V_{C1} = 2Ed \)
となる。
また,各コンデンサに蓄えられる電荷\(Q_{A1},Q_{B1},Q_{C1} \ \rm[C]\)の大きさは,
\( Q_{A1} = C_A \times V_{A1} = \displaystyle ε \frac{S}{d} \times Ed = ε SE \\ Q_{B1} = C_B \times V_{B1} = \displaystyle ε\frac{2S}{d}\times Ed = 2εSE \\ Q_{C1} = C_C \times V_{C1} = \displaystyle ε\frac{s}{2d} \times 2Ed =εSE\)
と表すことができる。
各コンデンサが蓄えている静電エネルギー\( W_{A1},W_{B1},W_{C1} \ \rm[J] \)の大きさは,
\( \begin{align} W_{A1} &= \displaystyle \frac{1}{2} Q_{A1} V_A \\ \\ &= \displaystyle \frac{1}{2} \times ε \displaystyle \frac{S}{d} \times Ed \times Ed \\ \\ &= \displaystyle \frac{1}{2}ε \displaystyle \frac{S}{d} E^2 d^2 \\ \\ &= \displaystyle \frac{1}{2} ε S E^2 d \\ \\ W_{B1} &= \displaystyle \frac{1}{2} Q_{B1} V_{B1} \\ \\ &= \displaystyle \frac{1}{2} \times ε \displaystyle \frac{2S}{d} \times Ed \times Ed \\ \\ &= εS E^2 d \\ \\ W_{C1} &= \displaystyle \frac{1}{2} Q_{C1} V_{C1} \\ \\ &= \displaystyle \frac{1}{2} \times ε \displaystyle \frac{S}{2d} \times 2Ed \times 2Ed \\ \\ &= ε S E^2 d \end{align}\)
電エネルギーの総和は,
\( \begin{align} W_1 &= W_{A1} + W_{B1} + W_{C1} \\ \\ &= \displaystyle \frac{1}{2} ε S E^2 d + εS E^2 d + εS E^2 d \\ \\ &= \displaystyle \frac{5}{2}εS E^2 d \end{align} \)
となる。
並列接続後の静電エネルギーの総和を求める
問題文より同じ極性で並列に接続したと記載があるので,コンデンサに蓄えられている電荷\(\ \rm[C]\)の変化は以下の様になる。
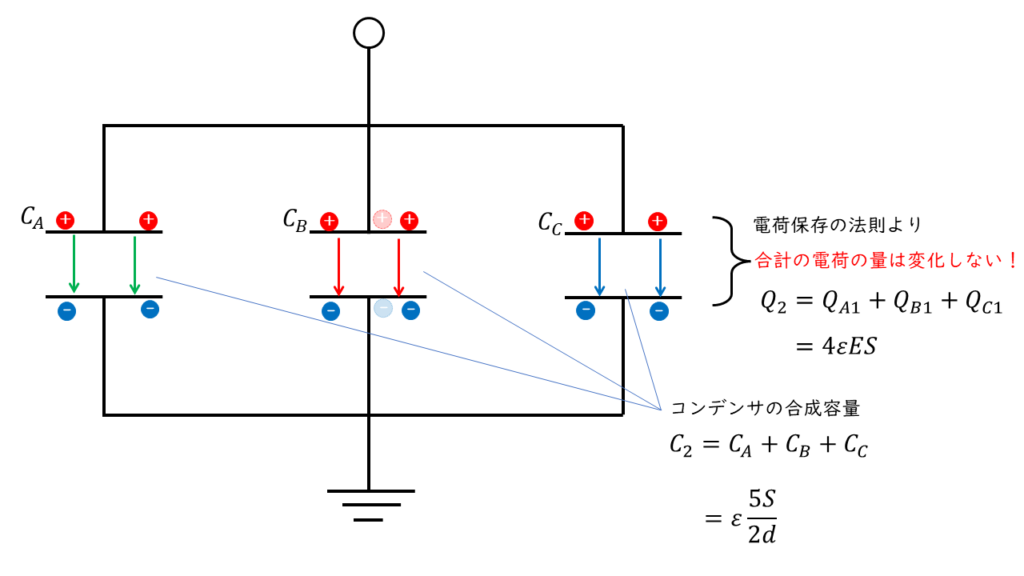
電荷保存の法則により,各コンデンサに蓄えられている合計の電荷の大きさは並列接続前と変わらない。
よって,並列接続後の電荷の合計は
\( \begin{align} Q_2 &= Q_A1 + Q_B1 + Q_C1 \\ &=εSE + 2εSE +εSE = 4εSE \end{align} \)
また、コンデンサの合成容量の大きさは,
\( \begin{align} C_2 &= C_A + C_B + C_C \\ \\ &= ε \displaystyle \frac{S}{d} + ε \displaystyle \frac{2S}{d} + ε \displaystyle \frac{S}{2d} \\ \\ &= ε \displaystyle \frac{S}{d} \times \left( 2+4+1 \right) = ε \displaystyle \frac{7S}{2d} \end{align} \)
と計算できる。
以上の結果から,並列接続後の静電エネルギーの総和は,
\( \begin{align} W_2 &= \displaystyle \frac{1}{2} \times \displaystyle \frac{Q_2 \ ^2}{C_2} \\ \\ &= \displaystyle \frac{1}{2} \times \displaystyle \frac{ \left( 4εSE \right)^2 }{\displaystyle ε\frac{7S}{2d}} \\ \\ &= \displaystyle \frac{25}{7}εSE^2 d \end{align} \)
となる。
並列接続後の静電エネルギーが並列接続前の何倍になるか求める。
\( \begin{align} \displaystyle \frac{W_2}{W_1} &= \displaystyle \frac{\displaystyle \frac{16}{7}εSE^2 d}{\displaystyle \frac{5}{2}εS E^2 d} \\ \\ &= \displaystyle \frac{16 \times 2}{7 \times 5} = 0.9142… \end{align} \)
したがって、正解は(2)の0.91 倍となる。











コメント