問題
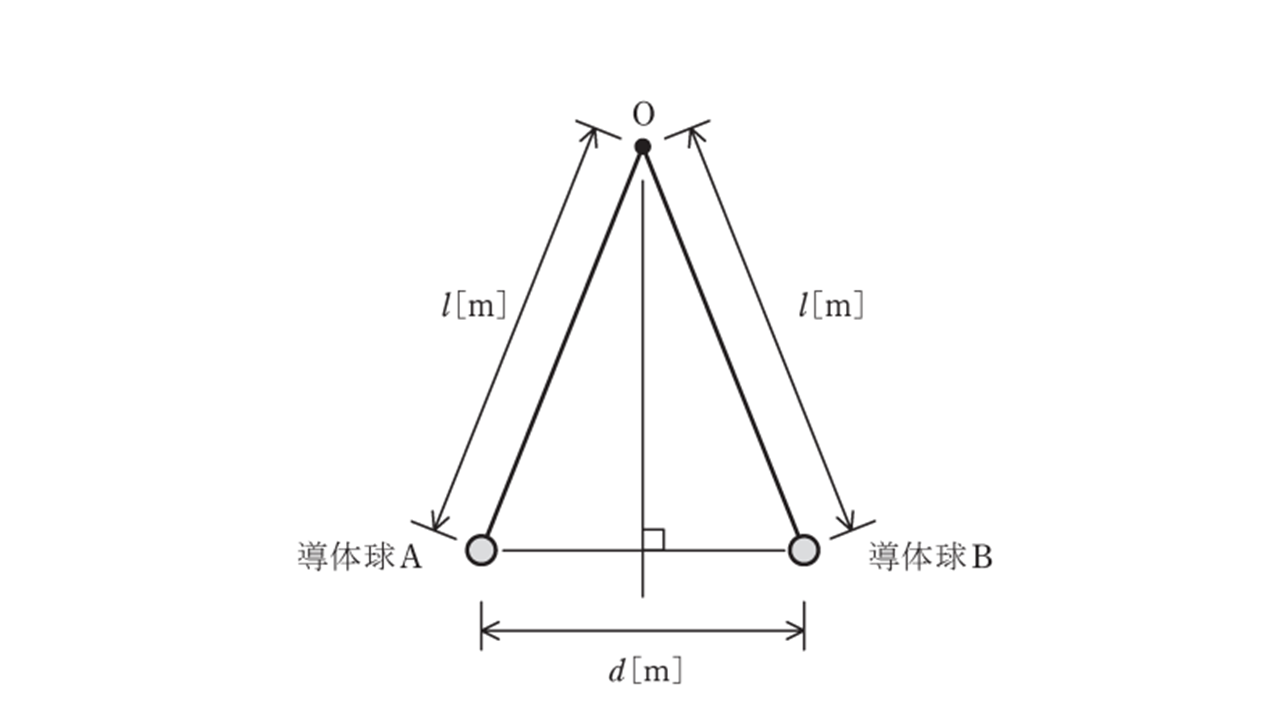
真空中で導体球A及びBが軽い絶縁体の糸で固定点Oから吊り下げられている。真空の誘電率を\(ε_0\ \rm[F/m]\),重力加速度を\(g\ \rm[m/s^2]\)とする。A及びBは同じ大きさと質量\(m\ \rm[kg]\)をもつ。糸の長さは各導体球の中心点が点Oからの距離\(l\ \rm[m]\)となる長さである。
まず,導体球A及びBにそれぞれ電荷\(Q\ \rm[C] \ ,3Q\ \rm[C]\)を与えて帯電させたところ,静電力による (ア) が生じ,図のようにA及びBの中心点間が\(d\ \rm[m]\)離れた状態で釣り合った。ただし,導体球の直径は\(d\)に比べて十分に小さいとする。このとき,個々の導体球において,静電力\(F=\) (イ) \(\ \rm[N]\),重力\(mg\ \rm[N]\),糸の張力\(T\ \rm[N]\),の3つの力が釣り合っている。三平方の定理より\(\ F^2 + (mg)^2 = T^2\) が成り立ち,張力の方向を考えると\(\displaystyle \frac{F}{T}\)は\(\displaystyle \frac{d}{2l}\) に等しい。これらより\(T\)を消去し整理すると,\(d\)が満たす式として,
\( k \left( \frac{d}{2l} \right)^3 = \sqrt{1- \left( \frac{d}{2l} \right) ^2}\)
が導かれる。ただし,係数\(k = \) (ウ) である。
次に,AとBとを一旦接触させたところAB間で電荷が移動し,同電位となった。AとBとの力の釣り合いの位置に戻った。接触前に比べ,距離\(d\)は (エ) した。
上記の記述中の空白箇所の(ア),(イ),(ウ)及び(エ)に当てはまる組み合わせとして,正しいものを次の(1)~(5)のうちから一つ選べ。
$$ \begin{array}{ccc} &(ア) &(イ) &(ウ) &(エ) \\ \hline (1) &反発力 &\frac{3Q^2}{4\pi ε_0 d^2} &\frac{16\pi ε_0 l^2 mg}{3Q^2} &増加 \\ \hline (2) &吸引力 &\frac{Q^2}{4\pi ε_0 d^2} &\frac{4\pi ε_0 l^2 mg}{Q^2} &増加 \\ \hline (3) &反発力 &\frac{3Q^2}{4\pi ε_0 d^2} &\frac{4\pi ε_0 l^2 mg}{Q^2} &増加 \\ \hline (4) &反発力 &\frac{Q^2}{4\pi ε_0 d^2} &\frac{16\pi ε_0 l^2 mg}{3Q^2} &減少 \\ \hline (5) &吸引力 &\frac{Q^2}{4\pi ε_0 d^2} &\frac{4\pi ε_0 l^2 mg}{3Q^2} &減少 \\ \hline \end{array}$$
解説
答え:(1)
(ア):静電力のはたらき
静電力(静電気力,クーロン力)は同じ符号の電荷同士では反発し,異なる符号同士では引き合う(吸引)性質があります。問題文中には、導体球Aは\(Q\ \rm[C]\),Bは\(3Q\ \rm[C]\)と記載があるため同じ符号であることが読み取れます。
よって(ア)に当てはまる言葉は,”反発力“になります。
(イ):静電力の大きさ
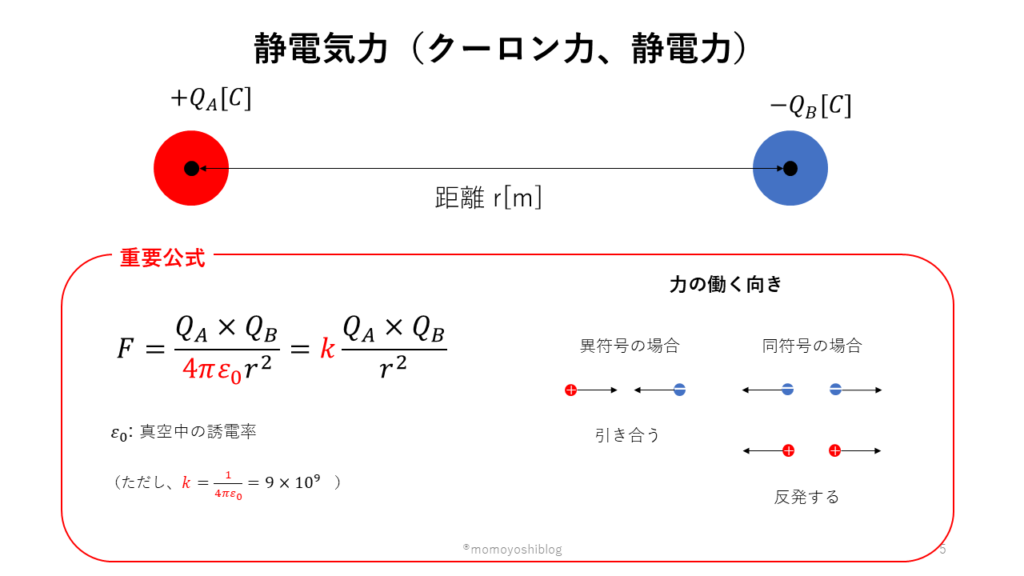
2つの電荷の間に働く静電力の大きさは以下の式で求めることができます。
$$ F = \frac{Q_A \times Q_B}{4\pi ε r^2} $$
ただし,\(ε\):誘電率,\(r\):2つの電荷間の距離とする。
この式に問で与えられている文字を代入していくと
$$ F = \frac{Q \times 3Q}{4\pi ε_0 d^2} = \frac{3Q^2}{4\pi ε_0 d^2} $$
が得られます。
(ウ):力の釣り合いによる式変形
問題文中では力の釣り合いにより以下の2つの式が与えられています。
$$ \begin{eqnarray} F^2 + \left( mg \right)^2 = T^2 \tag{1} \\ \frac{F}{T} = \frac{d}{2l} \tag{2} \end{eqnarray}$$
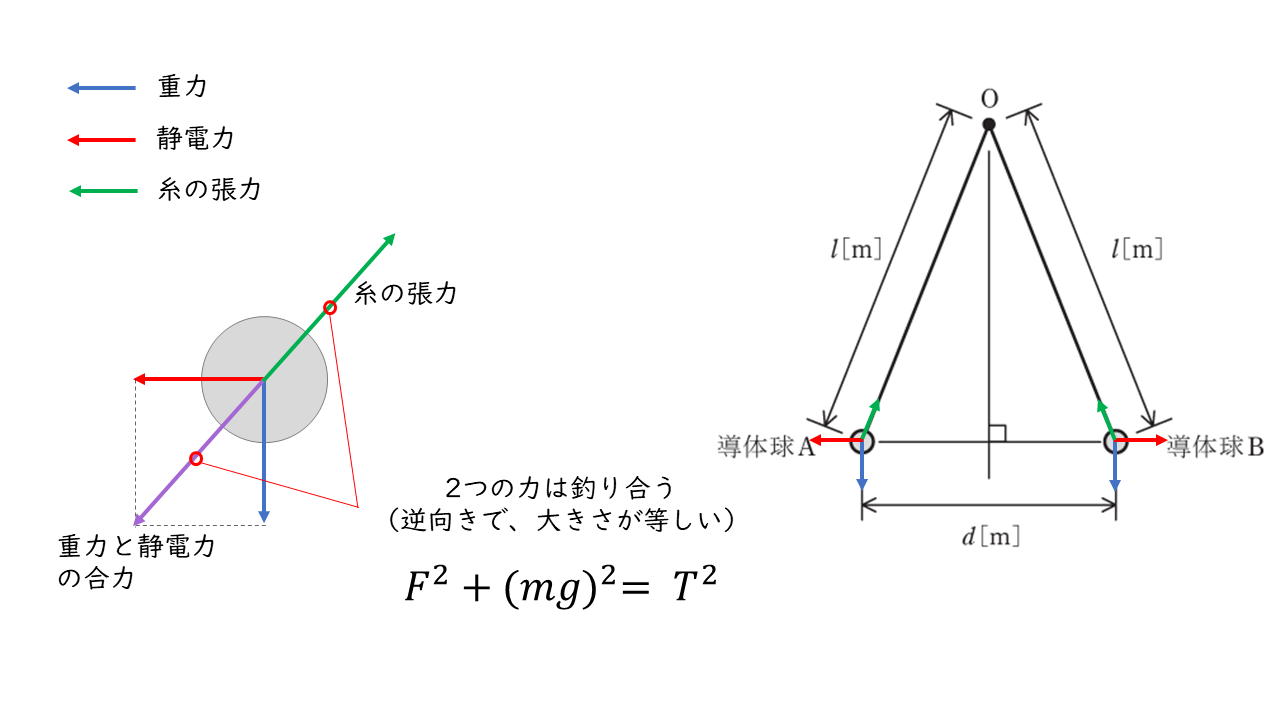
\((1)\)の式を変形し,\(\displaystyle \frac{F}{T} \)を代入できる形を作っていきます。
$$ \begin{align} F^2 + \left( mg \right)^2 &= T^2 \\ \left( \frac{F}{T} \right)^2 + \left( \frac{mg}{T} \right)^2 &= 1 \\ \left( \frac{d}{2l} \right)^2 + \left( \frac{d}{2lF} \times mg \right)^2 &= 1 \\ \left( \frac{dmg}{2lF} \right)^2 &= 1 – \left( \frac{d}{2l} \right)^2 \\ \frac{dmg}{2lF} &= \sqrt{ 1 – \left( \frac{d}{2l} \right)^2 } \end{align} $$
ここで,(イ)で求めた\( F = \displaystyle \frac{3Q^2}{4\pi ε_0 d^2}\) を代入すると以下の様に計算できます。
$$ \begin{align} \frac{dmg}{2l} \times \frac{4\pi ε_0 d^2}{3Q^2} &= \sqrt{ 1 – \left( \frac{d}{2l} \right)^2 } \\ \frac{d^3}{2l} \times \frac{4pi ε_0 mg }{3Q^2} &= \sqrt{ 1 – \left( \frac{d}{2l} \right)^2 } \\ \frac{d^3}{2l \times (2l)^2} \times \frac{4\pi ε_0 mg \times(2l)^2 }{3Q^2} &= \sqrt{ 1 – \left( \frac{d}{2l} \right)^2 } \\ \frac{4\pi ε_0 l^2 mg}{3Q^2} \times \left( \frac{d}{2l} \right)^3 &= \sqrt{ 1 – \left( \frac{d}{2l} \right)^2 } \end{align} $$
(エ):電荷が移動した後の静電気力の大きさ
導体球AとBの合計の電荷は\(4Q\ [C]\)です。2つの導体を接触させると電荷分布が均等になるように電荷の移動が起こります。導体球A及びBは同じ材質,同じ大きさであるから電荷の移動後は各導体球に\(2Q\ [C]\)ずつ電荷が蓄えられる状態になります。
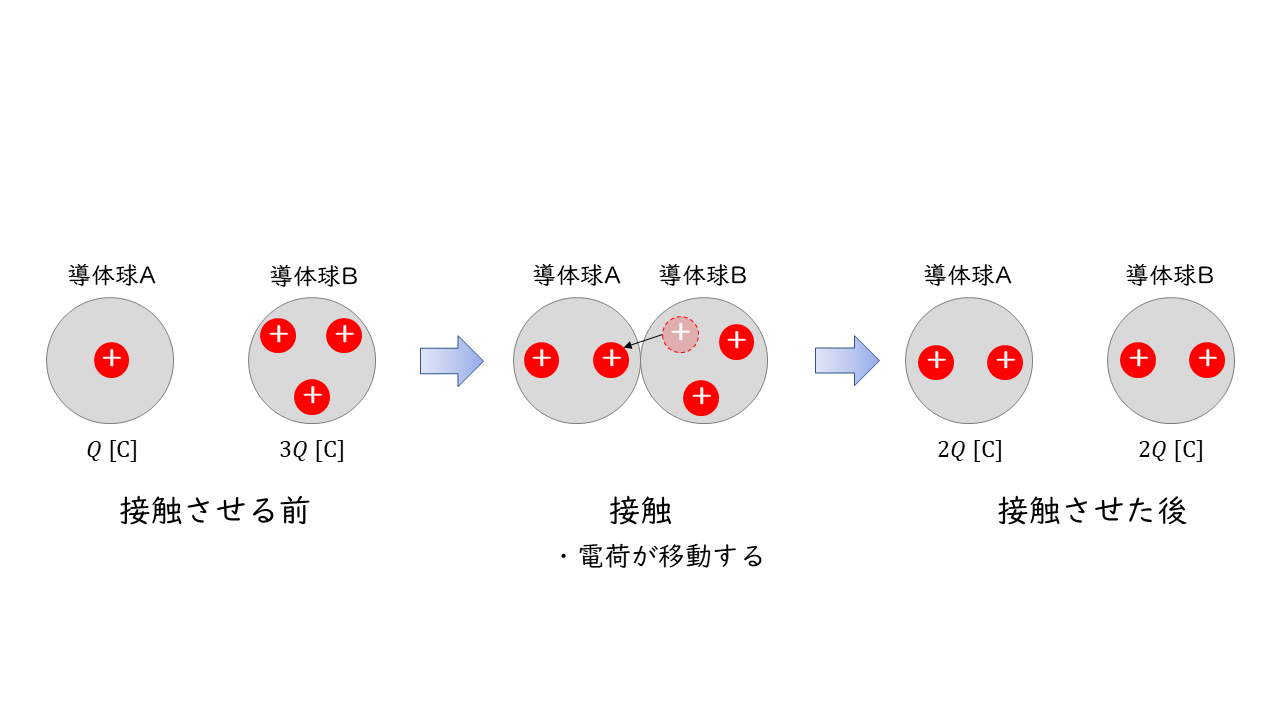
このときの静電力は,
$$ F = \frac{2Q \times 2Q}{4\pi ε_0 d^2} =\frac{4Q^2}{4\pi ε_0 d^2} $$
となり初めの状態よりも大きな静電力が働くことが分かります。
学習のポイント
2つの点電荷の間に働く静電気力の大きさ
静電力に関する問題は,計算が多く力学の知識が必要になる場合も多いです。静電気の分野においてコンデンサよりは出題頻度が低いですが,公式通りに当てはめることで回答が得られるので得点源になります。あきらめず少しずつ理解を深めていきましょう。











コメント