正解:(1)
問題
次の文章は,平行板コンデンサの電界に関する記述である。
極板間距離 \(d_0\ \rm[m]\)の平行板空気コンデンサの極板間電圧を一定とする。
極板と同形同面積の固体誘電体(比誘電率 \(ε_r > 1\),厚さ \(d_1\ \rm[m]<d_0\ \rm[m]\))を極板と平行に挿入すると,空気ギャップの電界の強さは,固体誘電体を挿入する前の値と比べて \(\fbox{ (ア) }\)。
また,極板と同形同面積の導体(厚さ \(d_2\ \rm[m] < d_0\ \rm[m]\))を極板と平行に挿入すると,空気ギャップの電界の強さは,導体を挿入する前の値と比べて\(\fbox{ (イ) }\)。
ただし,コンデンサの端効果は無視できるものとする。
上記の記述中の空白箇所(ア)及び(イ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
$$ \begin{array}{ccc} \ &(ア)&(イ) \\ \hline (1) &強くなる &強くなる \\ \hline (2) &強くなる &弱くなる \\ \hline (3) &弱くなる &強くなる \\ \hline (4) &弱くなる &弱くなる \\ \hline (5) &変わらない &変わらない \\ \hline \end{array}$$
解説
答え:(1)
空気ギャップとは平行平板コンデンサ内部の空気部分を指しています。空気の誘電率は,ほぼ1であるため,この問いでは,空気の誘電率≒真空中の誘電率として扱っています。
(ア) 誘電体挿入後の電界の大きさ
平行板コンデンサの両端にかかる電圧の大きさは一定であるから,極板間の電束の大きさも一定となる。(図1)
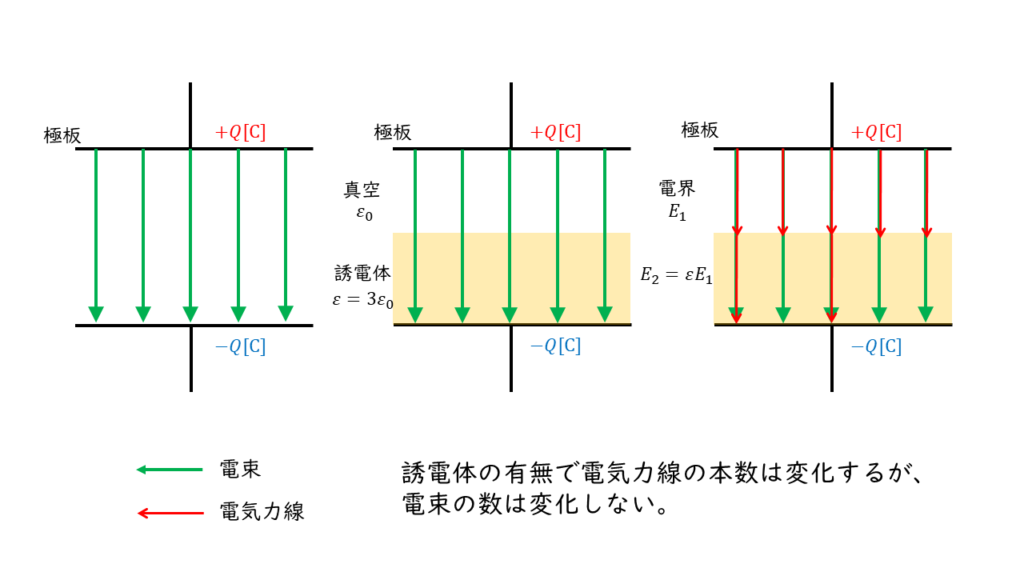
電界の強さ\(E\ \rm[V/m]\)は,電束\(D\)と誘電率\(ε\)を用いて次の式で表すことができる。
$$ E = \frac{D}{ε} \ \rm[V/m]$$
個体誘電体を挿入する前の極板間の電界の大きさ\(E_0\)は,真空中の誘電率\(ε_0\)を用いて
$$ E_0 = \frac{D}{ε_0} $$
と表すこととする。
個体誘電体を挿入した後のコンデンサ内部の様子は図2の様になる。
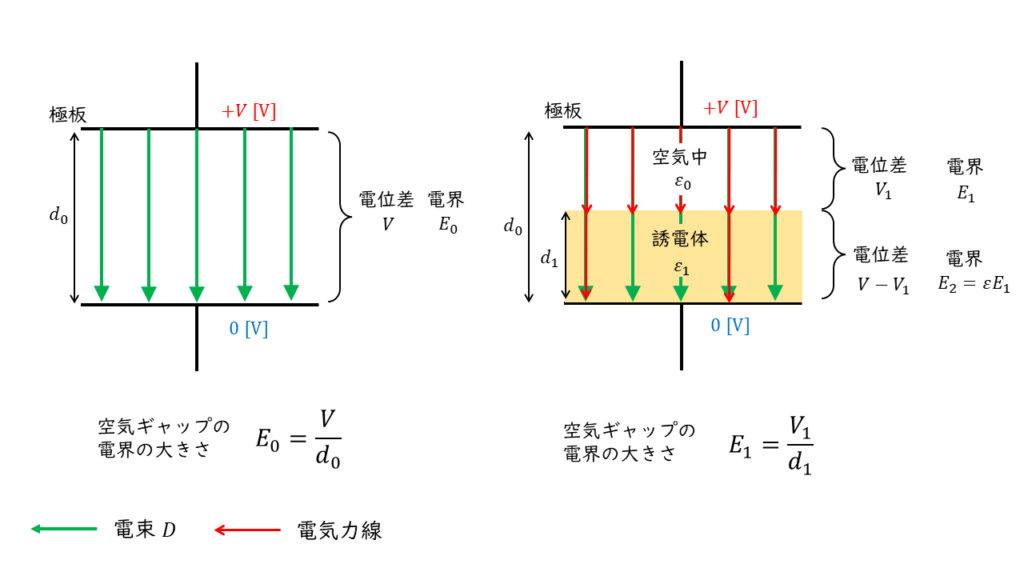
このときの空気部分の電界の大きさを\(E_1\),個体誘電体部分の電界の大きさを\(E_2\)とすると
\(\begin{eqnarray} E_1 = \frac{V_1}{d_0 – d_1} {1} \\ E_2 = \frac{V – V_1}{d_1} {2} \end{eqnarray} \)
と表すことができる。
極板間の電位差は変化しないことから,コンデンサ内部の電束も変化しないため
\( \begin{eqnarray} ε_r ε_0 E_2 &= ε_0 E_1 \\ E_2 &= \frac{E_1}{ε_r} {3} \end{eqnarray} \)
以上の(1)~(3)を使って個体誘電体挿入後の空気ギャップの電界の大きさ\(E_1\)を求める。
$$ \begin{align} V &= E_1 \times ( d_0 – d_1 ) + E_2 \times d_1 \\ &= E_1 \times ( d_0 – d_1 ) + \frac{E_1}{ε_r} \times d_1 \\ &= E_1 \times ( d_0 – d_1 + \frac{d_1}{ε_r} ) \\ E_1 &= \frac{V}{d_0 – d_1 \frac{d_1}{ε_r}} \end{align} $$
問題文より\(ε_r > 1 \)であるから,分母は必ず\(d_0\)よりも小さくなる。
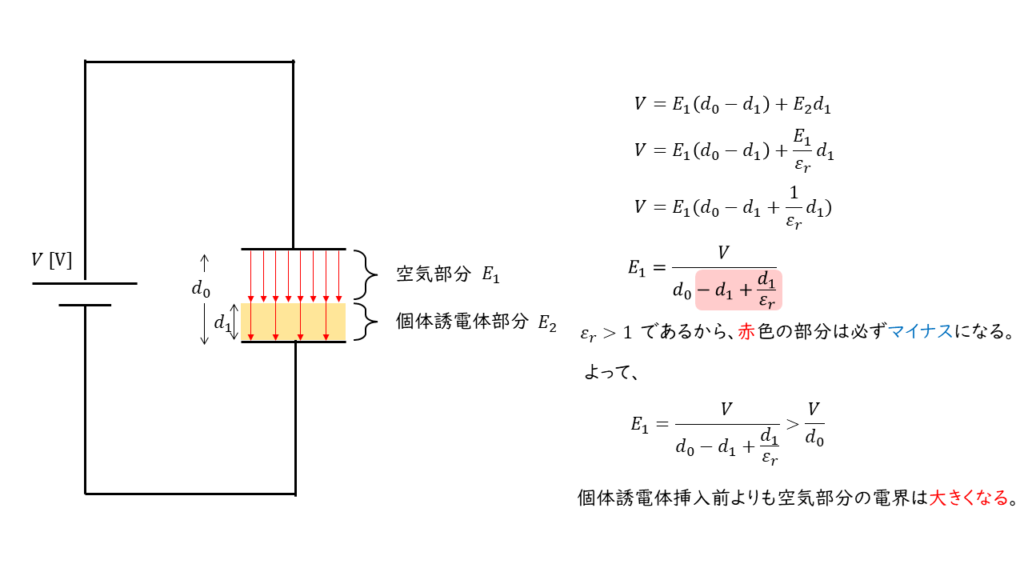
よって空気ギャップの電界の強さは個体誘電体の挿入後の方が大きくなる。
(イ) 導体挿入後の電界の大きさ
電界の大きさ\(E\)は極板間の電位差\(V\ \rm[V]\)と極板間の距離\(d\ \rm[m]\)を用いて次の様に表すことができる。
$$ E = \frac{V}{d} \ \rm[V/m] $$
極板間に導体を挿入した場合,コンデンサの極板間の距離は図4の様に変化する。
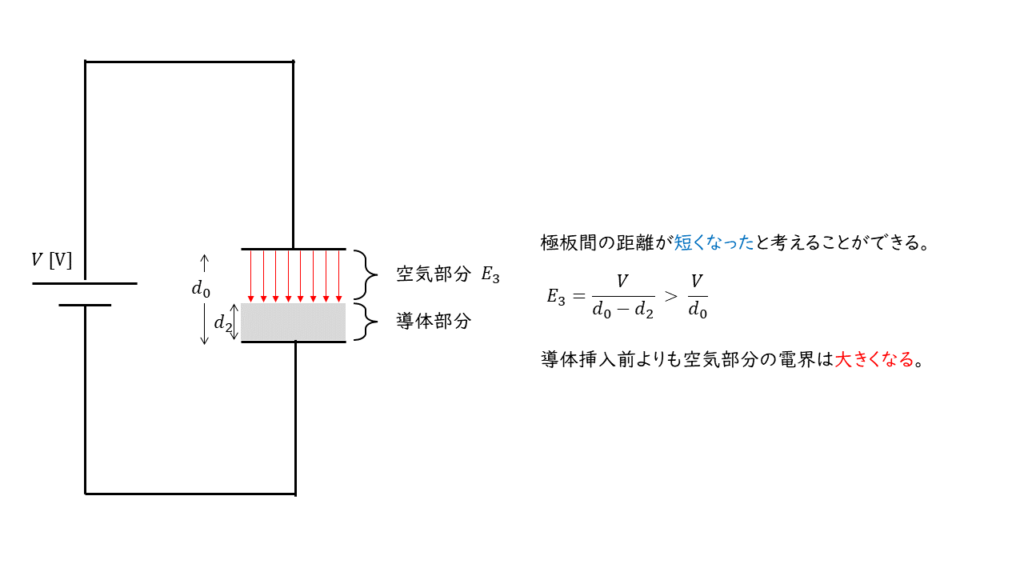
極板間の距離が短くなったと考えることができるので,問題文より\(d_2 \ \rm[m] < d_0 \ \rm[m] \)における空気ギャップの電界の大きさ\(E_3\)は
$$ E_3 = \frac{V}{d_0 – d_2} > \frac{V}{d_0} $$
となる。よって,導体挿入後の電界の強さ\(E_3\)は挿入前と比べ大きくなる。











コメント