問題
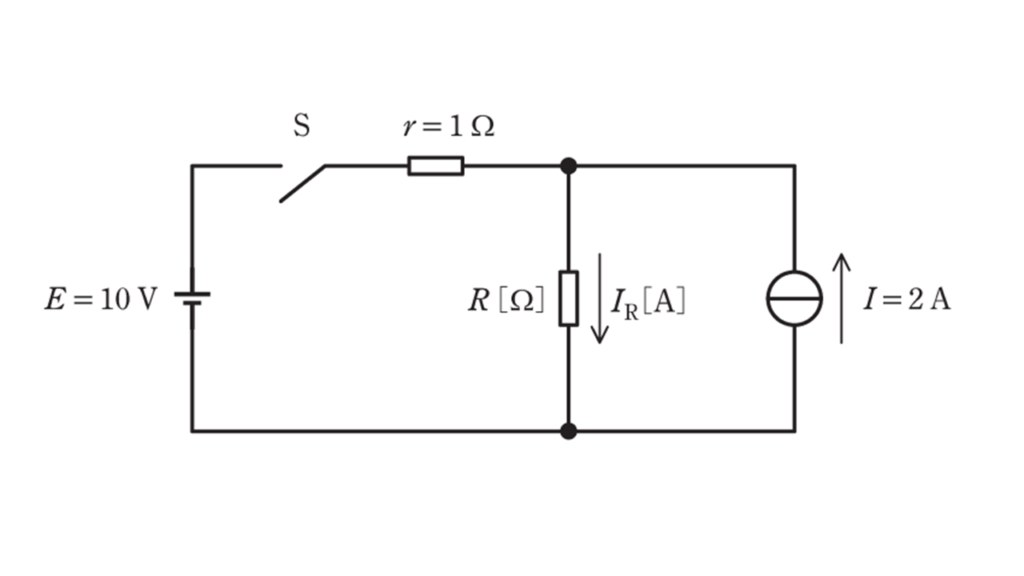
図のように,直流電圧 \(E=10\ \rm V\) の定電圧源,直流電流 \(I=2\ \rm A\) の定電流源,スイッチ\(\rm S\) , \(r=1\ \Omega\) と \(R\ [\Omega]\) の抵抗からなる直流回路がある。この回路において,スイッチ \(\rm S\) を閉じたとき, \(R\ [\Omega]\) の抵抗に流れる電流 \(I_R\) の値 [\(\rm A\)] が \(\rm S\) を閉じる前に比べて \(2\) 倍に増加した。\(R\) の値[\(\Omega\)]として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \(2\) (2) \(3\) (3) \(8\) (4) \(10\) (5) \(11\)
解説
答え:(1)
スイッチを閉じる前の電流を求める
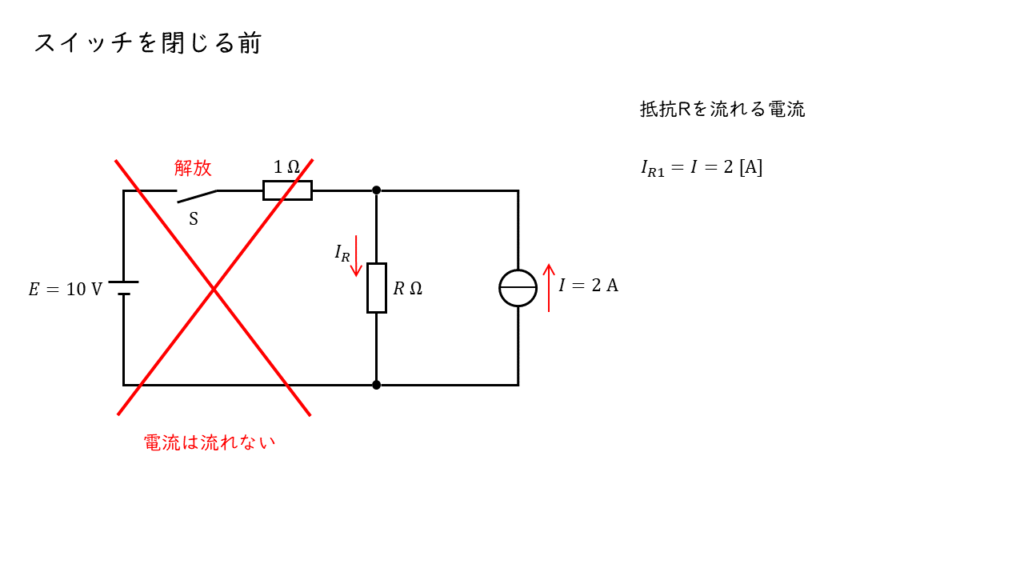
スイッチを閉じる前は,定電流源と抵抗 \(R\) のみが直接接続された直流回路であるから,抵抗 \(R\) に流れる電流 \(I_{R1}\) は,
\(I_{R1} = I = 2\ \rm A \cdots \cdots \left(1\right) \)
重ね合わせの理で考える
今回の問題のように電圧源や電流源が複数ある場合には、「重ね合わせの理」を使って計算することで簡単に解くことができます。
「重ね合わせの理」において,注目する1つの定電圧源または,定電流源以外はそれぞれ以下のように考えます。
定電圧源:「短絡状態」
定電流原:「解放状態」
よって,問いで与えられた回路図は以下の2つの回路を重ね合わせたものと考えることができます。
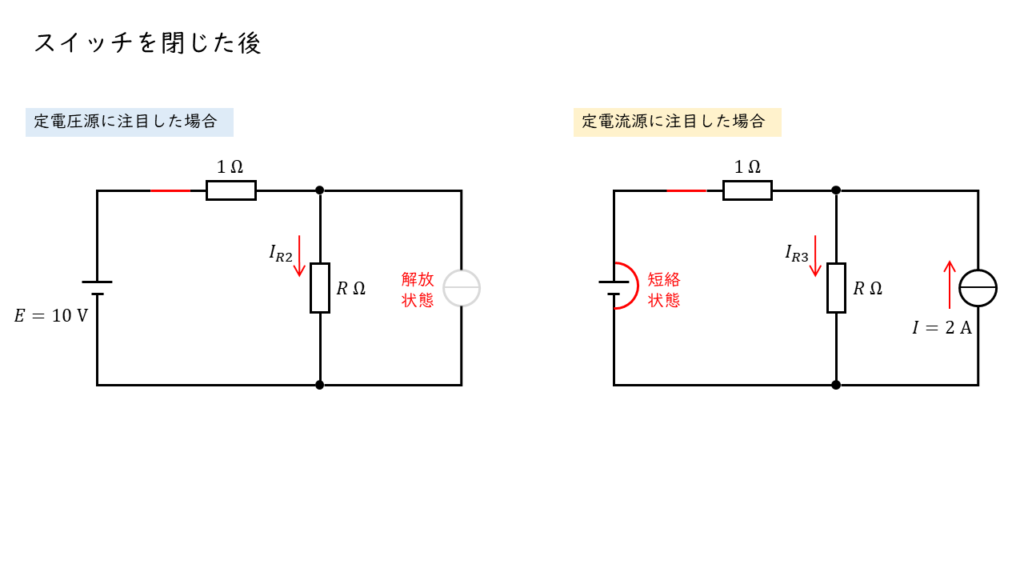
定電圧源に注目した場合
定電圧源に注目した場合,定電流源は「解放状態」とみなすことができるので,以下の直流回路を計算することで,抵抗 \(R\) を流れる電流 \(I_{R2}\) を求めることができます。
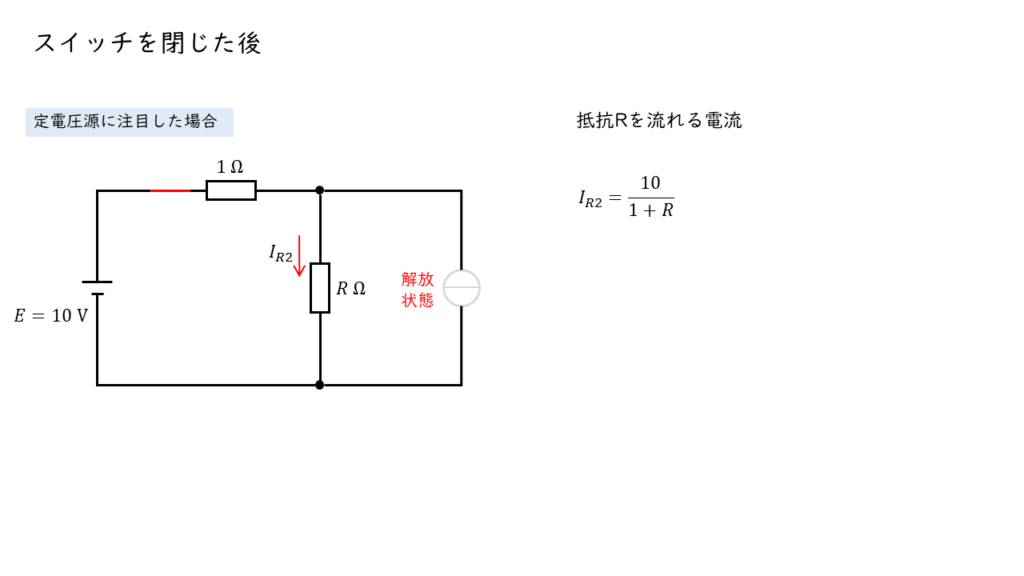
オームの法則より,
\(I_{R2} = \displaystyle \frac{10}{1 + R} \ \cdots \cdots \left(2\right) \)
と求めることができます。
定電流源に注目した場合
定電流源に注目した場合,定電圧源は「短絡状態」とみなすことができるので,以下の直流回路を計算することで,抵抗 \(R\) を流れる電流 \(I_{R2}\) を求めることができます。
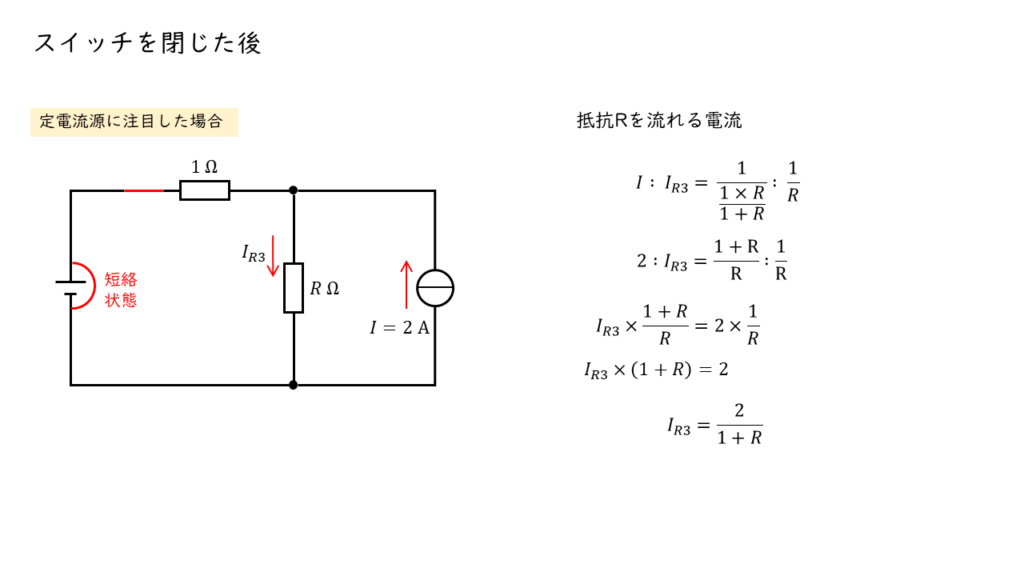
定電流源からは,常に回路に一定の(今回の問いでは \(2\ \rm A\) )電流が流れるので,定電流源から見て並列に接続された2つの抵抗には,抵抗値の逆数に比例した電流が流れます。
\(\begin{align} I : I_{R3} &= \displaystyle \frac{1}{\displaystyle \frac{R \times 1}{R+1}} : \displaystyle \frac{1}{R} \\ \\ \color{red}{ 2 } : I_{R3} &= \displaystyle \frac{R+1}{R} : \displaystyle \frac{1}{R} \\ \\ 2 \times \displaystyle \frac{1}{R} &= I_{R3} \times \displaystyle \frac{R+1}{R} \\ \\ 2 &= I_{R3} \times \left( R+1 \right) \\ \\ I_{R3} &= \displaystyle \frac{2}{R+1} \cdots \cdots \left(3\right) \end{align} \)
スイッチを閉じた状態での抵抗 \(R\) を流れる電流\(I_R\)を求める
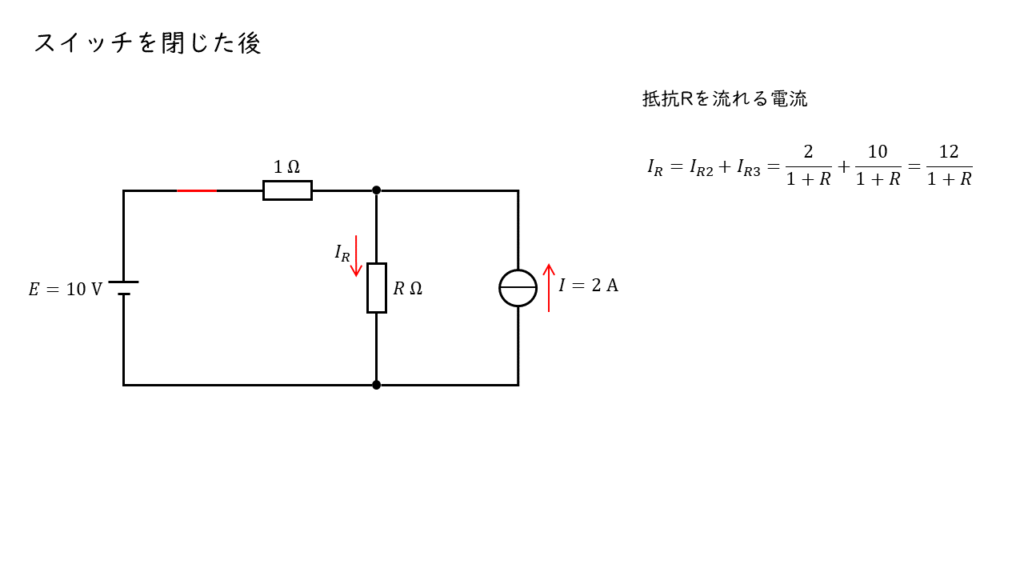
スイッチを閉じた状態での抵抗 \(R\) を流れる電流\(I_R\) の大きさは式(2),(3)より,
\(\begin{align} I_R &= I_{R2} + I_{R3} \\ \\ &= \displaystyle \frac{10}{1 + R} + \displaystyle \frac{2}{R+1} \\ \\ &= \displaystyle \frac{12}{R+1} \cdots \cdots \left(4\right) \end{align} \)
と計算することができます。
問いの条件より抵抗の値を計算する
問題文の条件より,スイッチ \(\rm S\) を閉じたときの電流 \(I_{R}\) は,スイッチを閉じる前の電流の2倍になったと記述があるので,式(1),(4)を用いて計算すると,
\(\begin{align} I_R &= 2 \times I_{R1} \\ \\ \displaystyle \frac{12}{R+1} &= 2 \times 2 \\ \\ 12 &= 4 \times \color{red}{ \left( R+1 \right) } \\ \\ 4R &= 12 \color{red}{ – 4 } \\ \\ 4R &= 8 \\ \\ R &= 2 \end{align} \)
よって,答えは(1)となります。










