問題
図に示す直流回路は, \(100 \ \rm V \) の直流電圧源に直流電流計を介して \(10 \ \rm \Omega \) の抵抗が接続され, \(50 \ \Omega \) の抵抗と抵抗 \(R \ [\Omega]\) が接続されている。電流計は \(5 \ \rm A \) を示している。抵抗 \(R \ [\Omega] \) で消費される電力の値 \(\rm [W] \) として,最も近いものを次の(1)~(5)のうちから一つ選べ。なお,電流計の内部抵抗は無視できるものとする。
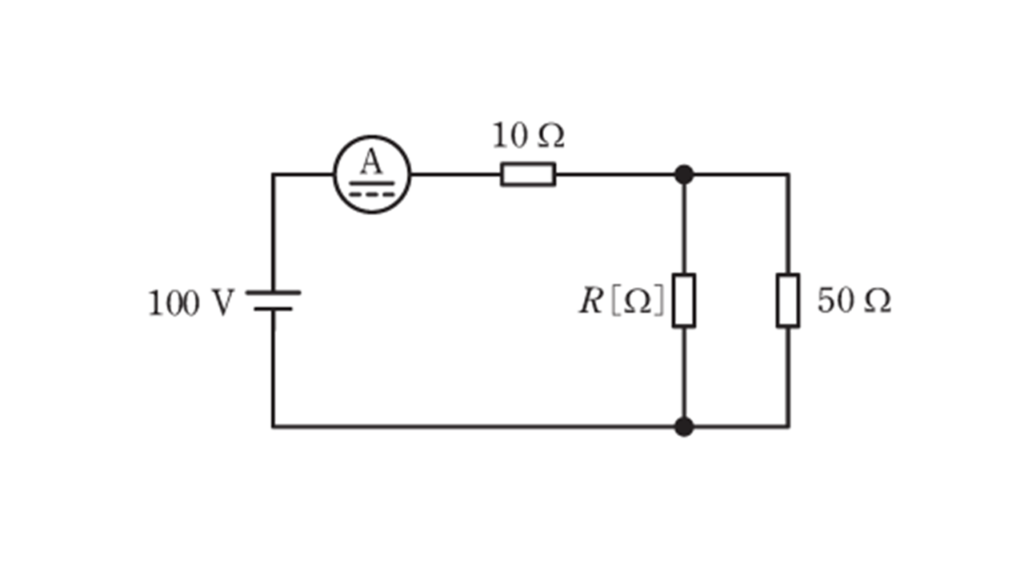
(1) \(2\) (2) \(10\) (3) \(20\) (4) \(100\) (5) \(200\)
解説
答え:(5)
抵抗 \(R\) の値を求める
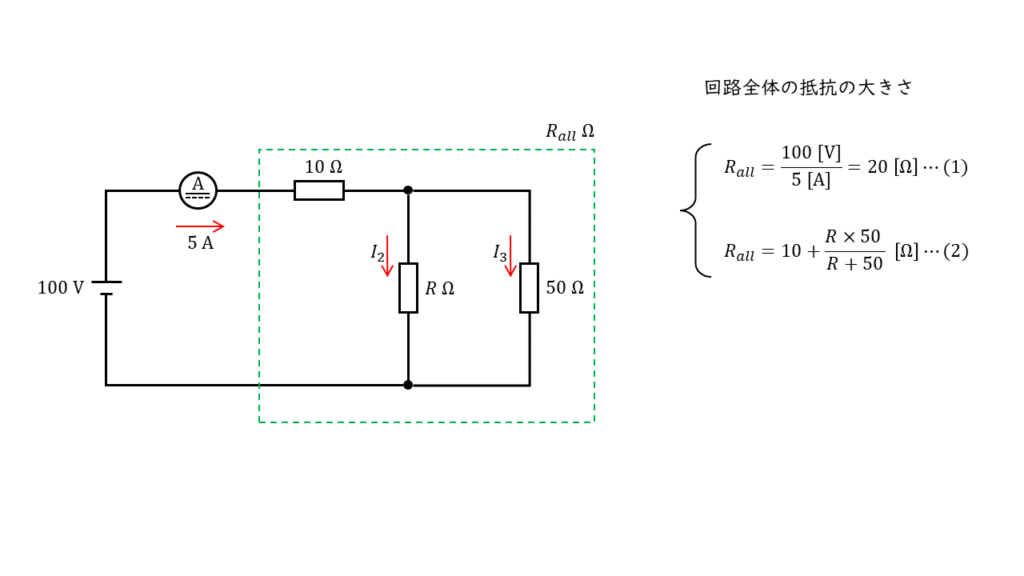
回路全体の抵抗の大きさを \(R_{all}\) とすると,以下の2つの式がたてられます。
\( R_{all} = \displaystyle \frac{100 \rm V}{5 \rm A} = 20 \Omega \tag{1} \)
\( R_{all} = 10 + \displaystyle \frac{R \times 50}{R + 50} \tag{2} \)
式(1),(2)より,
\(\begin{align} 20 \Omega &= 10 + \displaystyle \frac{R \times 50}{R+50} \\ \\ 10\color{red}{ \times \left( R + 50 \right) } &= 50R \\ \\ 10R+500 &= 50R \\ \\ 40R &= 500 \\ \\ R &=\displaystyle \frac{500}{40} \\ &= 12.5 \Omega \end{align} \)
抵抗 \(R\) に流れる電流の大きさを求める
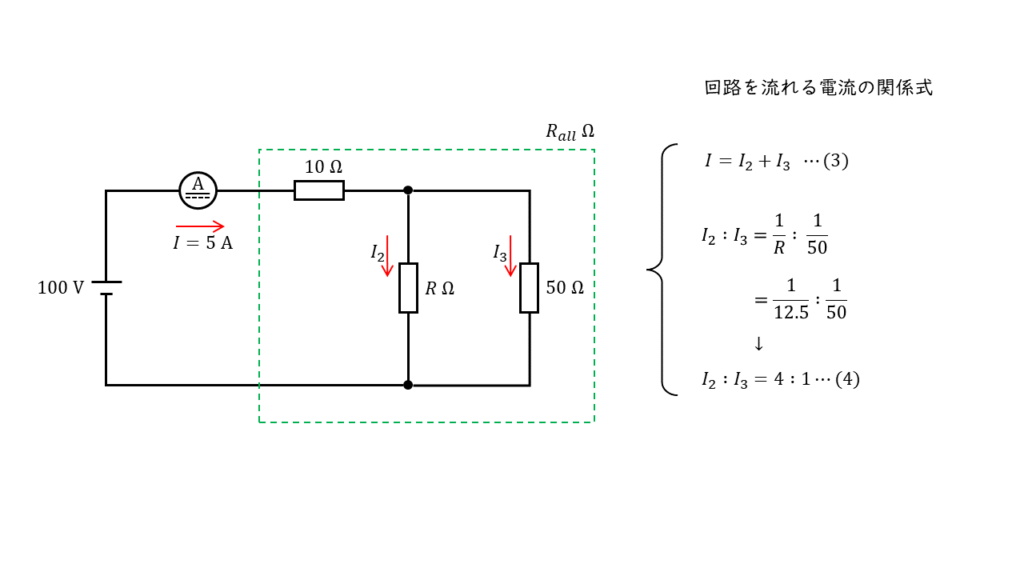
並列接続された2つの抵抗に流れる電流の比は,抵抗の逆数の比と等しくなるので,上図のように各抵抗を流れる電流をそれぞれ,\(I_2\) ,\(I_3\) と置くと,
\(\begin{align} I_2 : I_3 &= \displaystyle \frac{1}{12.5} : \displaystyle \frac{1}{50} \\ \\ I_2 : I_3 &= \displaystyle \frac{1}{12.5} \color{red}{ \times 50 } : \displaystyle \frac{1}{50} \color{red}{ \times 50 } \\ \\ I_2 : I_3 &= 4 : 1 \\ \\ I_2 &= 4I_3 \end{align} \)
となる。ここで,回路全体の電流の関係より,
\(\begin{align} I &= I_2 + I_3 \\ \color{red}{ 5 } &= \color{red}{ 4\times I_3 } +I_3 \\ 5 &= 5I_3 \\ I_3 &= 1 \rm A \end{align} \)
\(\begin{align} I_2 &= 5 – I_3 \\ &= 5 – 1 \\ &=4 \end{align} \)
と計算できます。
抵抗 \(R\) で消費される電力を計算する
抵抗で消費される電力は,(抵抗値)×(電流の二乗)で計算できるので,
\(\begin{align} P &= R \times I_2 ^2 \\ \\ &= 12.5 \times 4^2 \\ \\ &= 200 \rm W \end{align}\)
と計算できます。したがって,答えは(5)となります。










