問題
二つの導体小球がそれぞれ電荷を帯びており,真空中で十分な距離を隔てて保持されている。ここで,真空の空間を,比誘電率 2 の絶縁体の液体で満たしたとき,小球の間に作用する静電力に関する記述として,正しいものを次の(1)~(5)うちから一つ選べ。
(1) 液体で満たすことで静電力の向きも大きさも変わらない。
(2) 液体で満たすことで静電力の向きは変わらず,大きさは \(2\) 倍になる。
(3) 液体で満たすことで静電力の向きは変わらず,大きさは \(\displaystyle \frac{1}{2}\) 倍になる。
(4) 液体で満たすことで静電力の向きは変わらず,大きさは \(\displaystyle \frac{1}{4}\) 倍になる。
(5) 液体で満たすことで静電力の向きは逆になり,大きさは変わらない。
解説
答え:(3)
二つの小球それぞれに蓄えられている電荷の大きさを\(q_1\ [C]\)、\(q_2\ [C]\)、間の距離を\(r\ [m]\)、真空中の誘電率を\(ε_0 \ [F/m]\)で表すことにします。
二つの小球を真空中に置く場合
$$ F_0 = \frac{q_1 q_2}{4\pi ε_0 r^2} $$
二つの小球を比誘電率2の空間中に置く場合
$$ F_1 = \frac{q_1 q_2}{4 \pi ( 2\times ε_0) r^2} $$
2つの式を見比べると大きさは\(\displaystyle \frac{1}{2}\)となります。
また、静電気力の向きは蓄えられている電荷の+、-の組み合わせで決まります。問題文には電荷の+、-を変えた記載はないので、静電力の向きに変化はありません。
よって答えは(3)になります。
ポイント
2つの点電荷の間に働く静電気力の大きさ
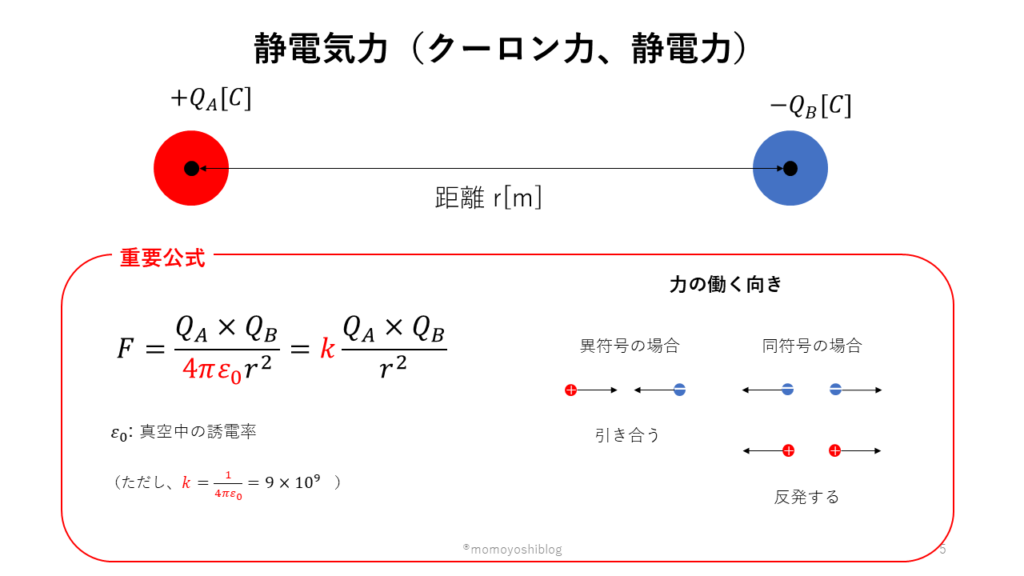
\(Q_A\ [C]\)の点電荷と\(Q_B\ [C]\)の点電荷の間に働く静電気力(静電力またはクーロン力)の大きさ\(F\ [N]\)は、2点間の距離を\(r\ [m]\)、誘電率を\(ε\ [F/m]\)とすると以下のように表すことができます。
$$ F = \frac{Q_A Q_B}{4\pi ε r^2}$$
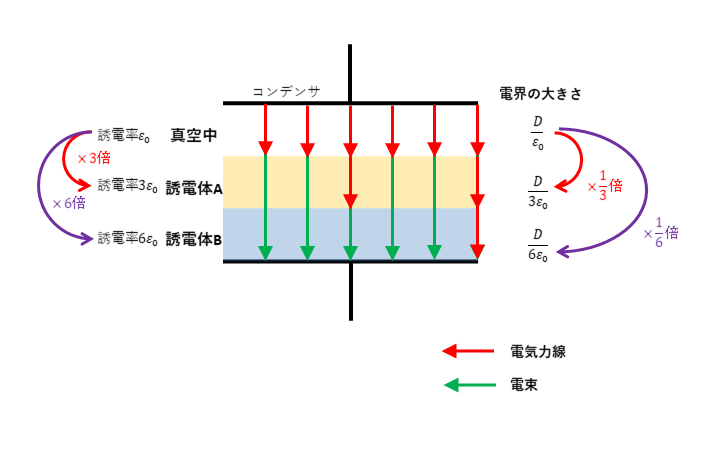
誘電率と比誘電率
誘電率とは、周りの空間の電気力線の透しにくさ(電界の強さをどのくらい緩和してくれるか)を表した値のことを指します。特に指定が無い場合には、真空中の誘電率と空気の誘電率は同じ大きさとして考えます。
$$ ε_0 = 8.85 \times 10^{-12} \ [F/m]$$
一方、比誘電率とは真空中の誘電率を基準(1として考える)としたとき、何倍になるかを表したものになります。したがって単位は無く比誘電率\(ε_1 = 3\)の場合、
$$ ε = 3 \times ε_0 = 3ε_0 $$
と表します。











コメント