問題
次の文章は,電磁誘導に関する記述である。
図のように,コイルと磁石を配置し,磁石の磁束がコイルを貫いている。
1 .スイッチ S を閉じた状態で磁石をコイルに近づけると,コイルには \( \fbox { (ア) } \) の向きに電流が流れる。
2 .コイルの巻数が 200 であるとする。スイッチ S を開いた状態でコイルの断面を貫く磁束を \(0.5\ \rm s\) の間に \(10\ \rm mWb\) だけ直線的に増加させると,磁束鎖交数は \( \fbox { (イ) } \) \(\rm Wb\) だけ変化する。また,この \(0.5\ \rm s\) の間にコイルに発生する誘導起電力の大きさは \( \fbox { (ウ) } \) \(\rm V\) となる。ただし,コイル断面の位置によらずコイルの磁束は一定とする。
上記の記述中の空白箇所(ア)~(ウ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
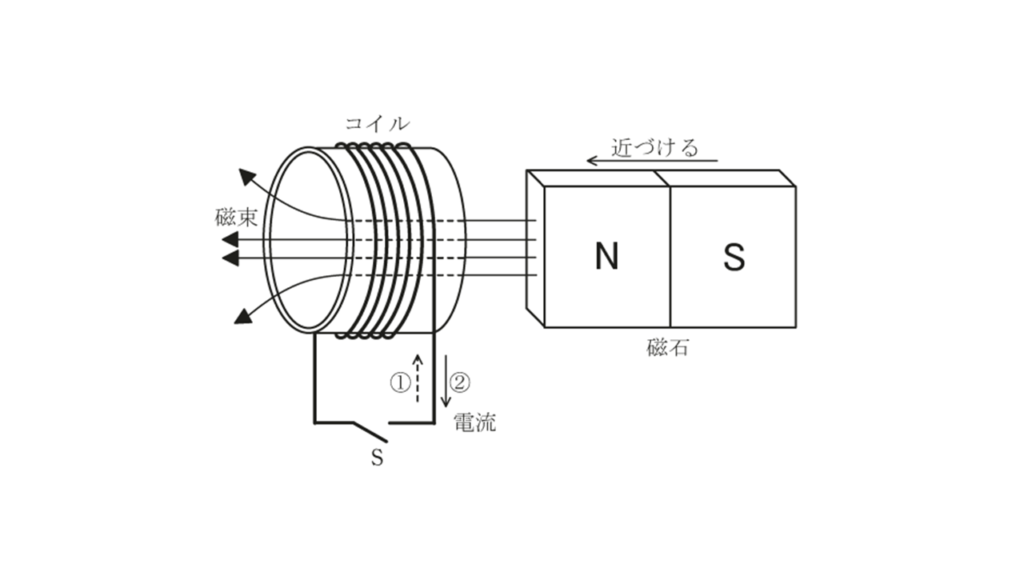
$$ \begin{array}{cccc} \ &(ア)&(イ)&(ウ)\\ \hline (1) &① &2 &2 \\ \hline (2) &① &2 &4 \\ \hline (3) &① &0.01 &2 \\ \hline (4) &② &2 &4 \\ \hline (5) &② &0.01 &2 \\ \hline \end{array} $$
解説
答え:(4)
(ア)コイルに流れる電流の向き
コイルは,磁束の変化を嫌うため,N極を近づけると反対向きの磁束を発生させる方向に電磁誘導による電流が流れます。
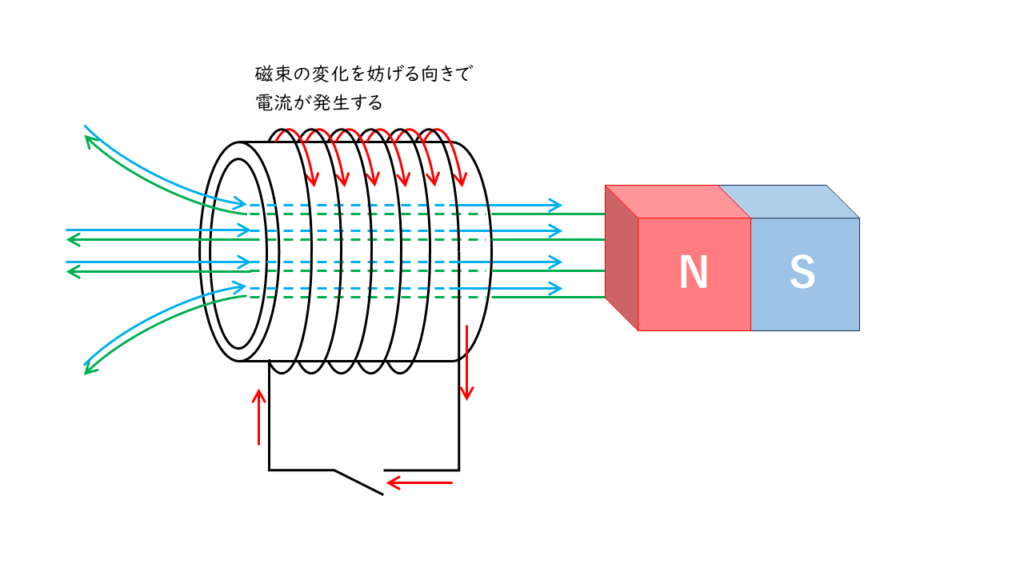
問の条件では,上図のように②の方向に電流が発生します。
(イ)磁束鎖交数を求める
磁束鎖交数 \( \Phi \) とは,コイルを貫く磁束の本数のことを言います。コイルの巻数を \(N\) 回 ,磁束の大きさを \( m \ \rm [Wb]\) とすると,
\( \Phi = N \times m = 200 \times 10 \times 10^{-3} = 2 \)
と計算することができます。
(ウ)誘導起電力の大きさ
誘導起電力 \(e \ \rm [V]\) は,1秒当たりのコイルを貫く磁束の本数の変化によって決まるため,コイルの巻数を \(N\) 回,磁束の変化の大きさを \( \Delta m\ \rm [Wb]\) ,時間の変化の大きさ \(\Delta t \ \rm[s]\)とすると,
\(\begin{align} e &= N \displaystyle \frac{\Delta m}{\Delta t} \\ \\ &= 200 \times \displaystyle \frac{10 \times 10^{-3}}{0.5} \\ \\ &= 4 \ \rm[V] \end{align} \)











コメント