問題
面積がともに \(S\ \rm[m^2] \) で円形の二枚の電極板(導体平板)を、互いの中心が一致するように間隔 \(d\ \rm[m]\) で平行に向かい合わせて置いた平行板コンデンサがある。
電極板間は誘電率 \(ε\ \rm[F/m]\) の誘電体で一様に満たされ、電極板間の電位差は電圧 \(V\ \rm [V]\) の直流電源によって一定に保たれている。この平行板コンデンサに関する記述として、誤っているものを次の(1)~(5)のうちから一つ選べ。
ただし、コンデンサの端効果は無視できるものとする。
(1) 誘電体内の等電位面は、電極板と誘電体の境界面に対して平行である。
(2) コンデンサに蓄えられる電荷量は、誘電率が大きいほど大きくなる。
(3) 誘電体内の電界の大きさは、誘電率が大きいほど小さくなる。
(4) 誘電体内の電束密度の大きさは、電極板の単位面積当たりの電荷量の大きさに等しい。
(5) 静電エネルギーは誘電体内に蓄えられ、電極板の面積を大きくすると静電エネルギーは増大する。
解説
答え:(3)
(1)正しい
平行板コンデンサ内の電界(電気力線)の様子は、図1のように極板に対して全て垂直になっています。
「等電位面」は電気力線と直角に交わるので、図2のようになります。
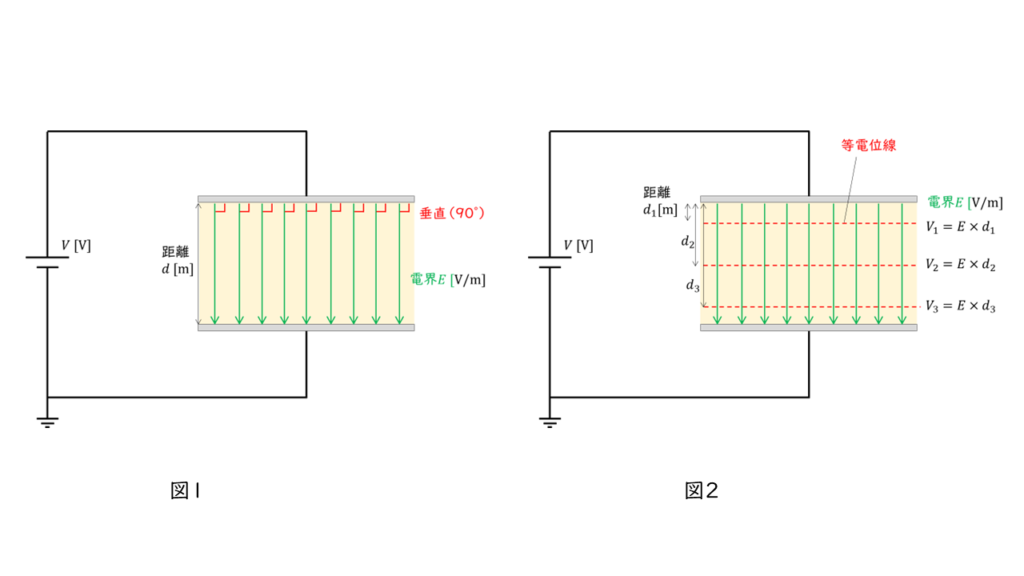
したがって、「等電位面」は電極板と誘電体の境界面に対して平行になります。
(2)正しい
コンデンサの電荷の蓄えやすさ(静電容量)\( C \ \rm[F]\)は、問題で与えられた記号を用いて表すと、
\( C = ε \displaystyle \frac{S}{d} \ \rm[F] \)
になります。電圧\(V \ \rm[V]\)の電源と接続されているので、コンデンサに蓄えられる電荷量\(Q \ \rm[C]\)は、
\( Q = C \times V = ε\displaystyle \frac{S}{d} \times V \)
と表すことができ、誘電率\(ε\)に比例することが分かります。
(3)誤り
コンデンサが電源と接続されている場合、コンデンサの極板間には、どこであっても電界の大きさが一定になる、「平等電界」が生じます。
そのため、「…誘電率が大きいほど小さくなる。」の一文は誤りです。
次の2つの式の使い分けを理解しておきましょう。
\( E = \displaystyle \frac{V}{d} \tag{1} \)
\( E = \displaystyle \frac{Q}{4\pi ε r^2} \tag{2} \)
コンデンサが電源と接続されている場合、極板間には、電位差\(V \ \rm[V]\)が生じるので、(1)の式を使用します。
コンデンサが充電した状態で電源と切り離された場合、コンデンサには\(Q\ \rm[C]\)の電荷が蓄えられたまま残るので、(2)の式を使用します。
コンデンサが電源と接続されているときの電界の式を考える
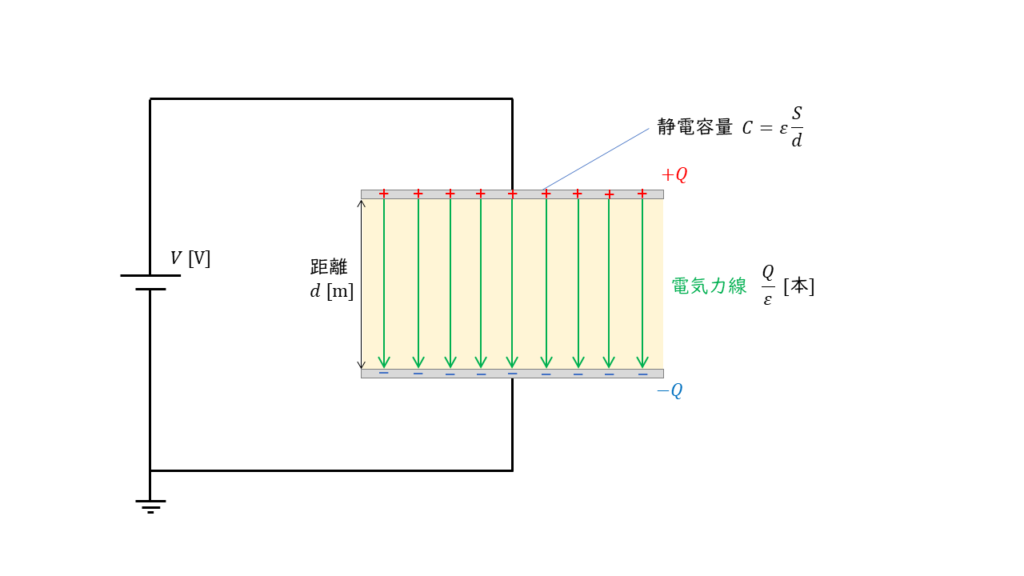
コンデンサの静電容量は、
\( C = ε\displaystyle \frac{S}{d} \)
となり、蓄えられる電荷量\(Q \ \rm[C]\)は、
\( Q = C \times V = ε\displaystyle \frac{SV}{d}\)
となります。極板から出る電気力線の本数\(\phi\)は、
\( \phi = \displaystyle \frac{Q}{ε} = \displaystyle \frac{SV}{d} \)[本]
よって、電界の大きさは、
\( E = \displaystyle \frac{\phi}{S} = \displaystyle \frac{V}{d} \)
となり、電源の電圧と極板間の距離にのみ依存する式が得られます。
このため、電源と接続されたコンデンサ内部の電界は「平等電界」となるのです。
(4)正しい
電束とは、電荷の周り物質に関係なく、電荷\(Q\ \rm[C]\)から\(Q\)[本]の線(電束)がでると考えたものです。よって、電束と電荷量の大きさと等しくなります。
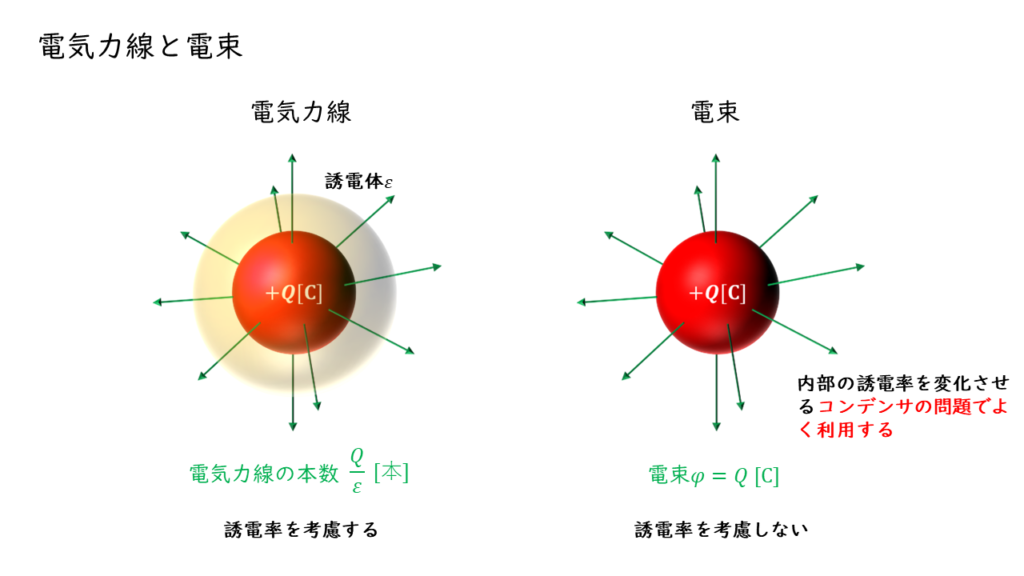
電束密度の大きさは、極板の単位面積当たりの電束の大きさのことなので、極板の単位面積当たりの電荷量の大きさと等しくなります。
(5)正しい
静電エネルギー\(W\)とは、充電されたコンデンサが持っているエネルギーのことです。
静電エネルギー:\( W = \frac{1}{2}QV = \frac{1}{2}CV^2 \) [J]
ここで、静電容量\(C \ \rm[F]\)は、面積\(S\ \rm[m^2]\)と極板間距離\(d\ \rm[m]\)、誘電率\(ε\ \rm[F/m]\)を用いて
\( C = ε \displaystyle \frac{S}{d} \ \rm[C] \)
と表すことができるので、静電エネルギーは誘電率の大きさに比例していると考えることができます。











コメント