問題
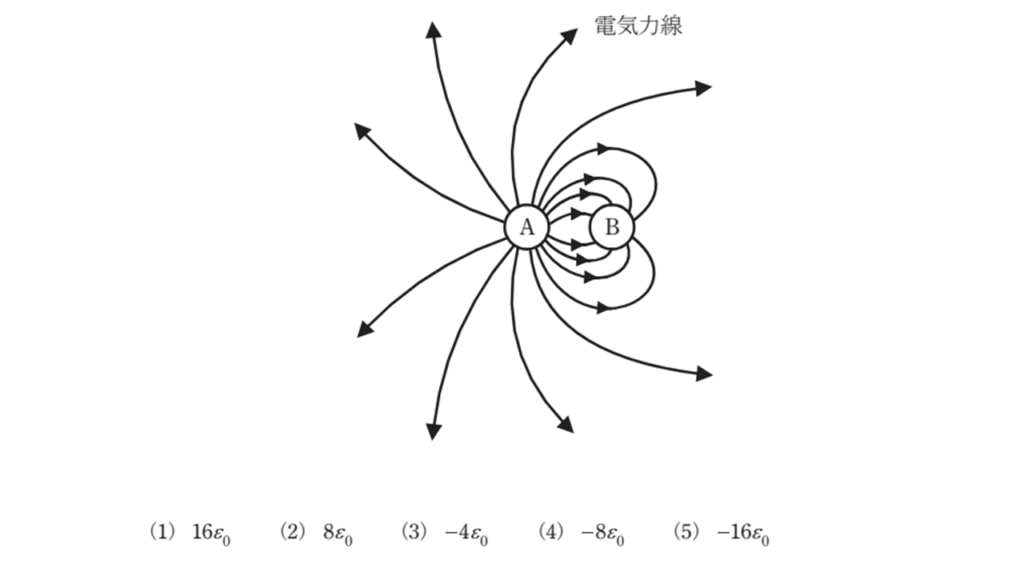
図に示すように、誘電率 \(ε_0\) [F/m] の真空中に置かれた二つの静止導体球 A 及び B がある。電気量はそれぞれ\( Q_A\) [C] 及び\( Q_B\) [C] とし,図中にその周囲の電気力線が描かれている。
電気量\( Q_A = 16ε_0\) [C] であるとき、電気量\( Q_B\) [C] の値として,正しいものを次の(1)~(5)のうちから一つ選べ。
解説
答え:(4)
\( Q_B\)の電荷の正、負を求める
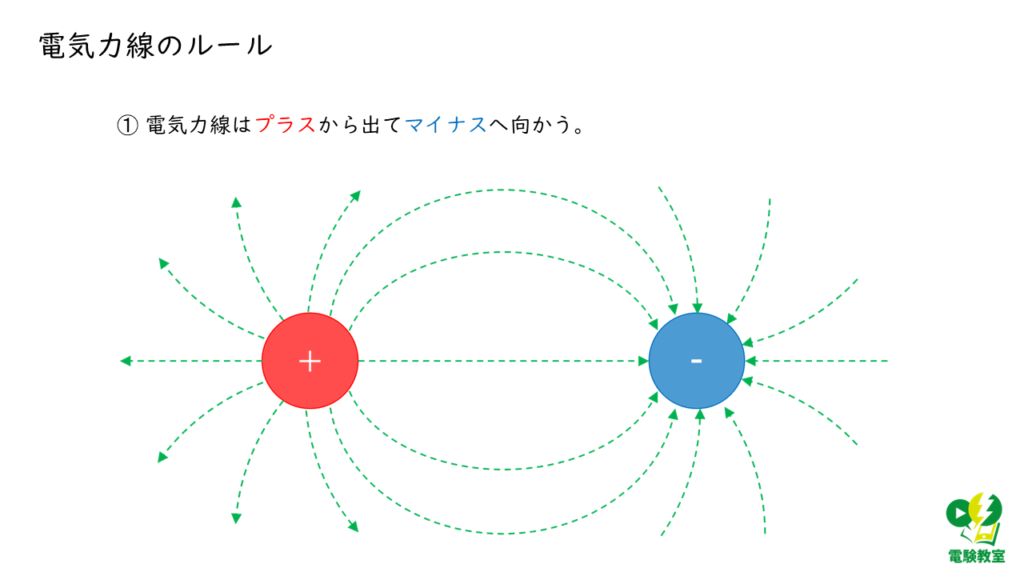
問題の図より電気力線は、\(Q_A\)から出て、\(Q_B\)に向かっています。
電荷の符号が異なるとき、電気力線はプラスの電荷から出て、マイナスの電荷向かうので、電荷\(Q_B\)の符号は、マイナスであることが分かります。
電気力線の本数から\(Q_B\)の電荷の大きさを求める
電気力線の本数は、電荷を\(Q\)[C]、誘電率を\(ε\)[F/m]とすると以下の式で求めることができます。
電気力線の本数 \( = \displaystyle \frac{Q}{ε}\) [本]
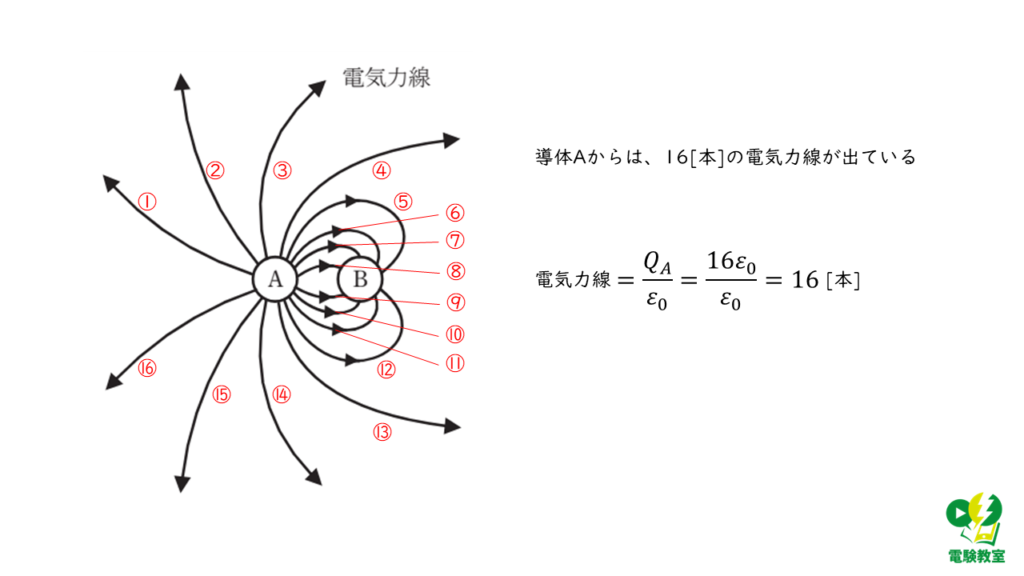
電荷\(Q_A\)から出ている電気力線の本数は、
\( \displaystyle \frac{Q_A}{ε_0} = \displaystyle \frac{16 ε_0}{ε_0} = 16\)[本]
と計算でき、問題の図と一致します。
一方、電荷\(Q_B\)の電気力線の本数は、問題の図より、8 [本]となっています。
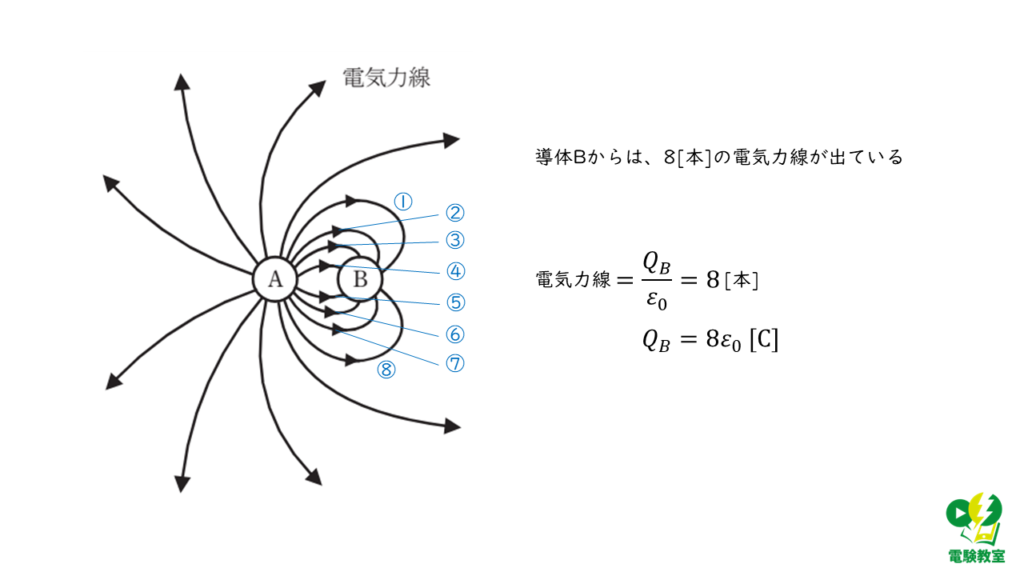
したがって、\(Q_B\)の大きさは、
\( \begin{align} \displaystyle \frac{Q_B}{ε_0} &= 8 \\ \\ Q_B &= 8 ε_0 \end{align} \)
と計算できます。
以上、2つの結果から、電荷\( Q_B\)は\( -8ε_0\)となります。











コメント