問題
図のように、平行板コンデンサの上下極板に挟まれた空間の中心に、電荷 \(Q\) [C] を帯びた導体球を保持し、上側極板の電位が\( E\) [V] 、下側極板の電位が\( −E\) [V] となるように電圧源をつないだ。ただし、\(E>0\) とする。同図に、二つの極板と導体球の間の電気力線の様子を示している。
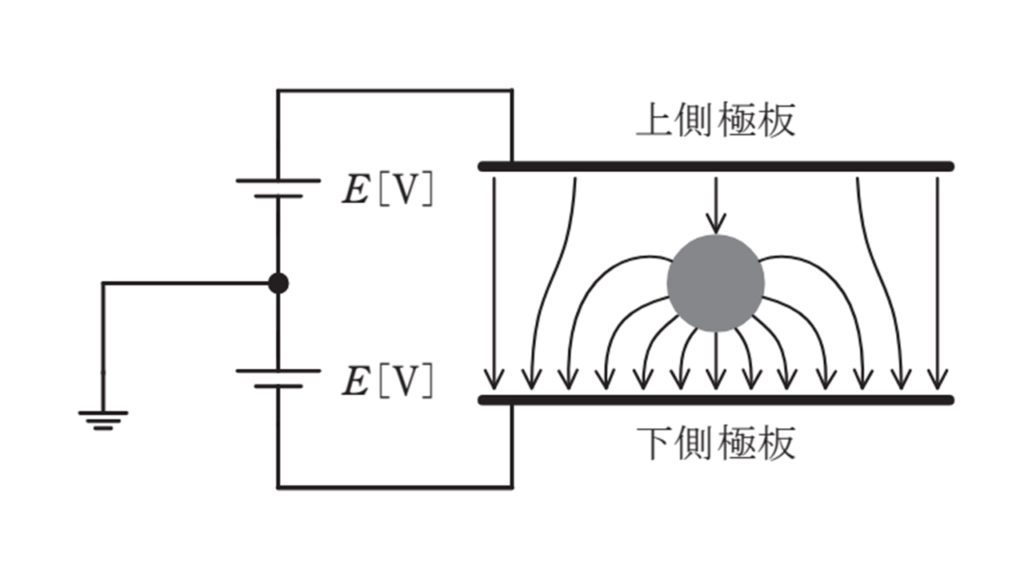
このとき、電荷\( Q\) [C] の符号と導体球の電位\( U\) [V] について、正しい記述のものを次の(1)~(5)のうちから一つ選べ。
(1) \( Q>0\)であり、 \(0<U<E\)である。
(2) \(Q>0\)であり、\(U=E\)である。
(3) \(Q>0\)であり、 \(0<E<U\)である。
(4) \(Q<0\)であり、\(U<−E\)である。
(5) \(Q<0\)であり、\(−E<U<0\)である。
解説
電荷\(Q\)[C]の符号について
問題の図より、電荷\(Q\)から出た電気力線は、マイナスに帯電している下側極板へ向かっていることが読み取れます。
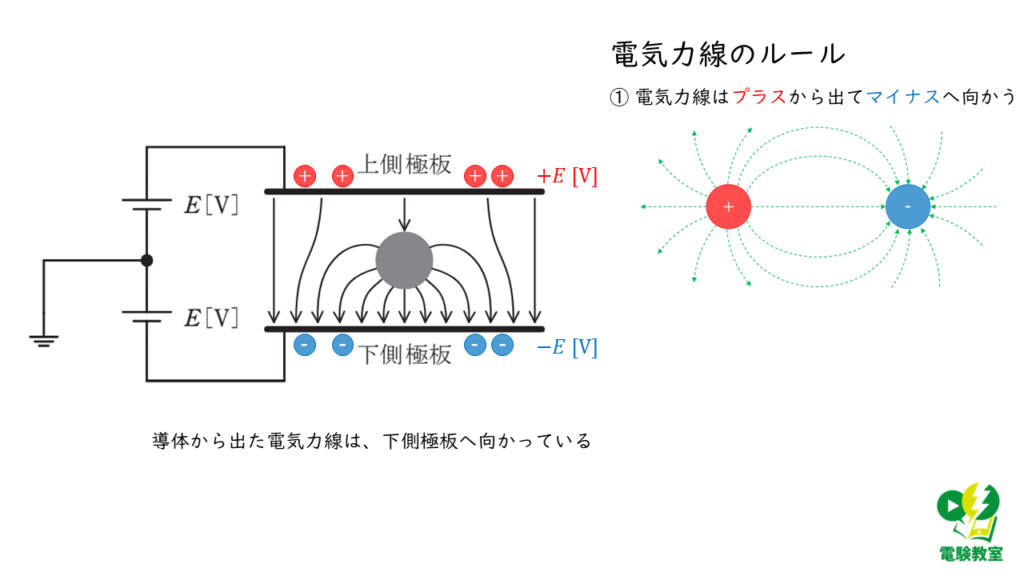
電気力線のルールより、「電気力線はプラスから出て、マイナスに向かう」ので、電荷\(Q\)の符号は、プラス\(\left( Q > 0 \right) \)であることが分かります。
電位\(U\)[V]の大きさについて
問題文の図より、下側極板に向かってくる電気力線の本数は、\(Q\)[C]帯電している導体から出る電気力線の本数よりも多くなっています。
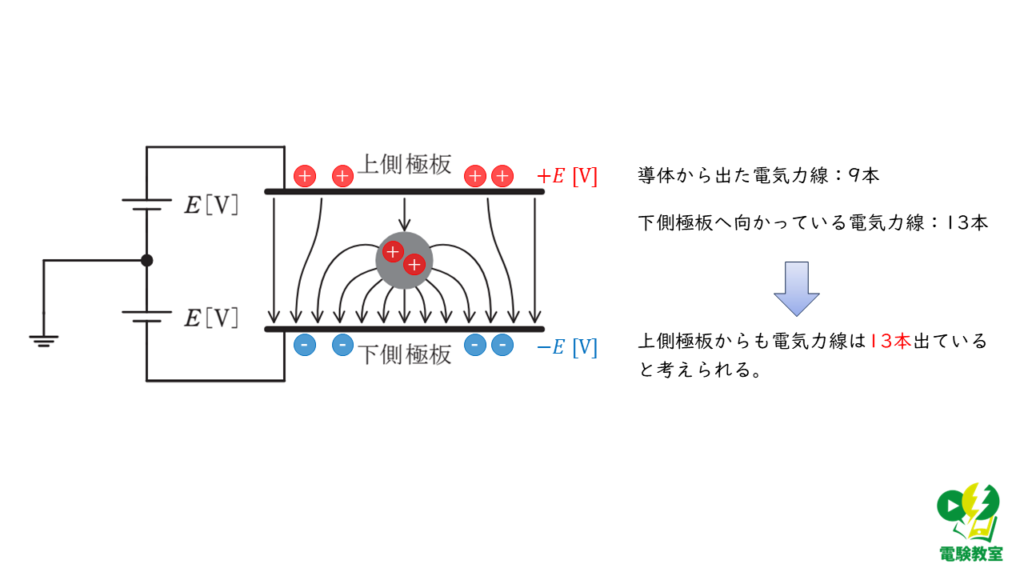
このことから、\(E\)[V]の電位がかかっている上側極板から出る電気力線の本数は、\(Q\)[C]帯電している導体から出ている電気力線の本数よりも多いと考えられます。
電気力線の本数は、電荷を\(Q\)[C]、誘電率を\(ε\)[F/m]とすると、
\( \displaystyle \frac{Q}{ε}\)
で求めることができました。電気力線の本数が多いということは、電荷の量が多いことを表しています。
電位の式は、電位を\(V\)[V]、電荷を\(Q\)[C]、誘電率を\(ε\)[F/m]、基準からの距離\(r\)[m]とすると、以下の式で表すことができます。
\( V = \displaystyle \frac{Q}{4 \pi ε r}\)
電位は、電荷が大きいほど大きくなるので、電荷の量が多い上側極板の方が導体より電位が大きいと考えられます。
したがって、電位の大きさは、\( E > U > 0\)となります。











コメント