問題
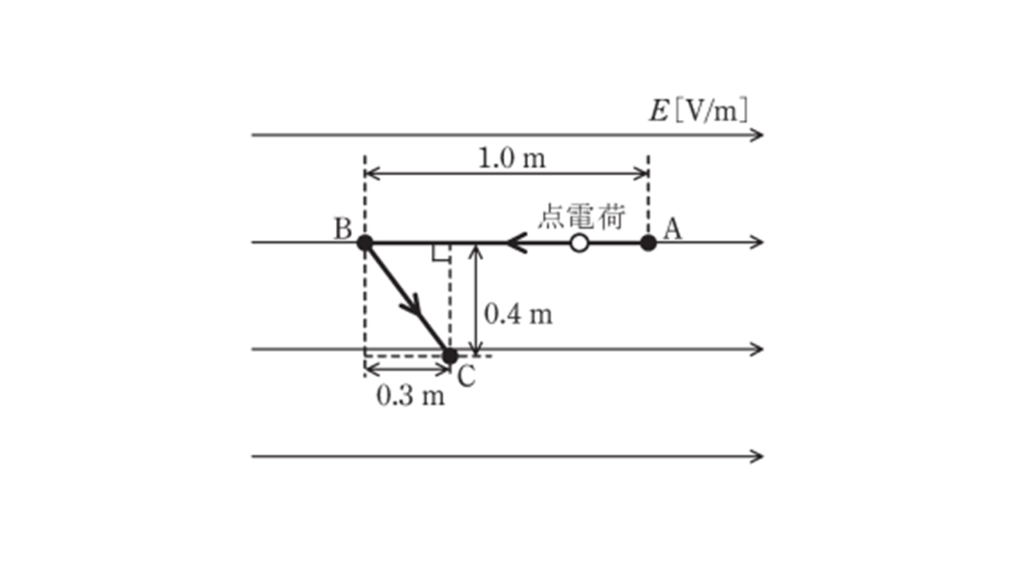
図のように,紙面に平行な平面内の平等電界 \(E\) [V/m] 中で \(2\) C の点電荷を点 A から点 B まで移動させ,さらに点 B から点 C まで移動させた。この移動に,外力による仕事 \(W=14\ \rm J\) を要した。点 A の電位に対する点 B の電位 \(V_{BA}\) [V] の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,点電荷の移動はゆっくりであり,点電荷の移動によってこの平等電界は乱れないものとする。
(1) \(5\) (2) \(7\) (3) \(10\) (4) \(14\) (5) \(20\)
解説
解答:(3)
問題文より点電荷を点A~Cまで移動させたときの仕事の大きさが\(14\ [J]\)とあるので、電位差と仕事の関係式より
$$ \begin{align} W &= Q \times V_{AC} \\ 14 &= 2 \times V_{AC} \\ V_{AC} &= \frac{14}{2} =7\ [V] \end{align} $$
となります。
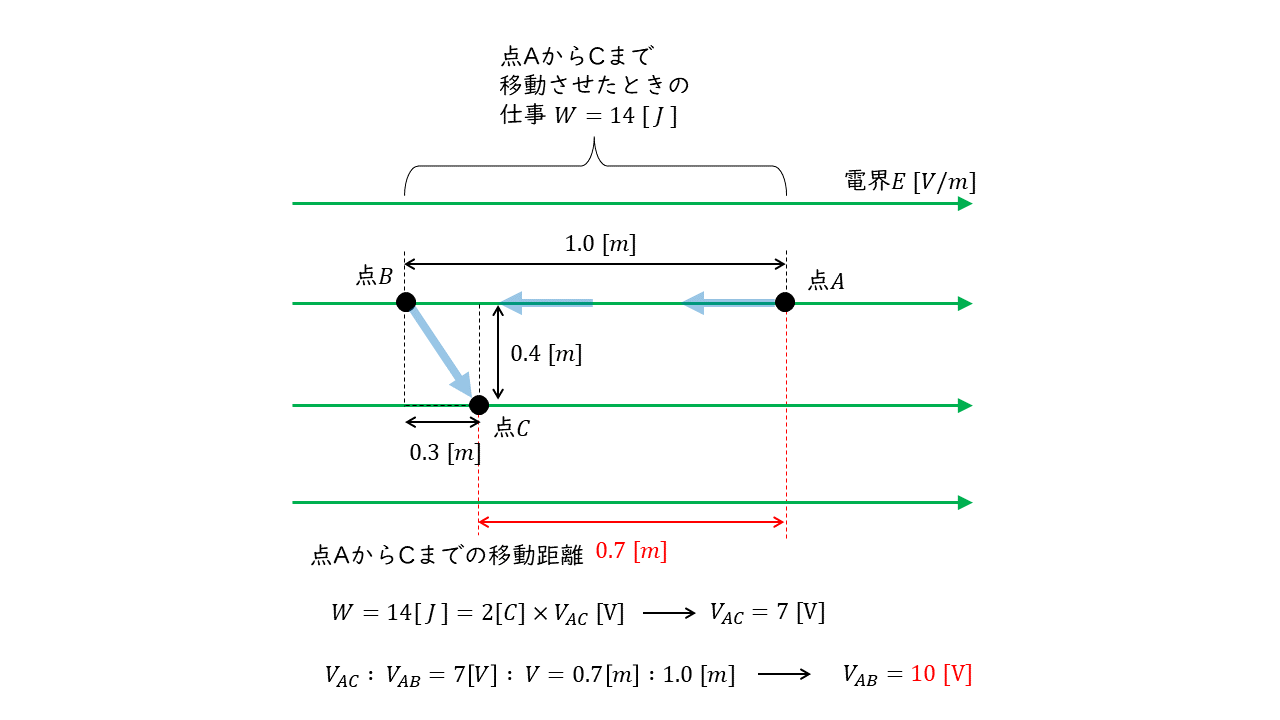
図より、点Aと点Cの電界\(E\ [V/m]\)に対して逆らう方向の距離の差\(d_{AC}\)は、
$$ d_{AC} = 1.0 – 0.3 = 0.7\ [m]$$
となるので、\(0.1\ [m]\)あたりの電位差\(V\ [V]\)(電界\(E\ [V/m]\)の大きさは以下の様に求めることができます。
$$ E = \frac{V_{AC}}{d_{AC}} = \frac{7}{0.7} = 10\ [V/m]$$
したがって、点AB間の電位差\(V_{AB}\ [V]\)の大きさは、
$$ V_{AB} = E \times d_{AB} = 10 \times 1.0 = 10\ [V] $$
になり、答えは(3)です。
ポイント
電位と仕事の関係を理解しよう
電位とは、電気的な位置の高さを表すものになります。よって基準とする地点からの垂直な距離の差のみが電位に影響を与えます。
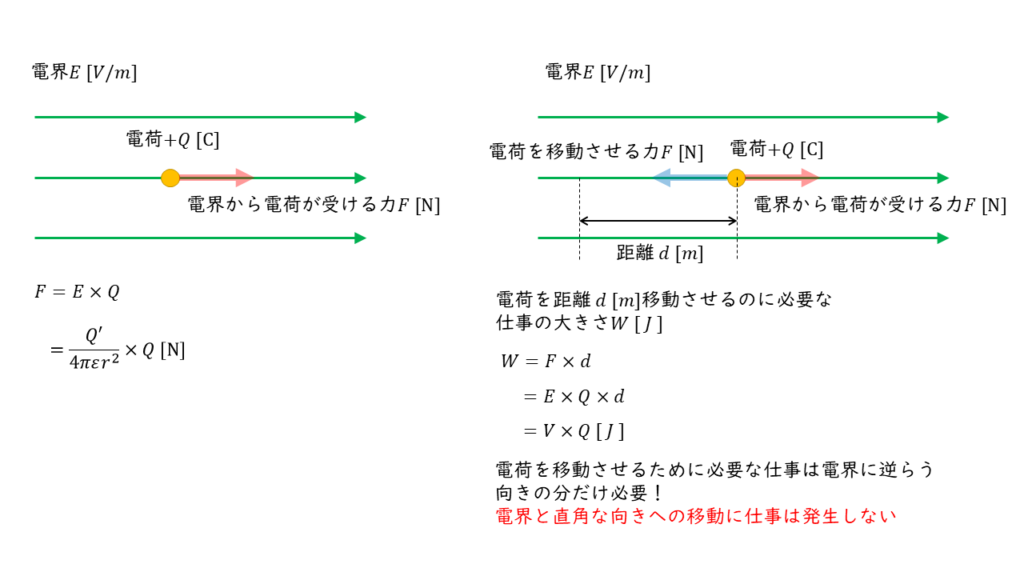
電界\(E\ [V/m]\)と電位差\(V\ [V]\)の関係
電界\(E\ [V/m]\)に逆らって\(+1[C]\)の点電荷を移動させるときに必要な仕事の大きさが電位差\(V\ [V]\)となります。電界\(E\ [V/m]\)中において、移動前の地点をA点、移動後の地点をB点、2点の間の距離を\(d\ [m]\)としたとき、2点の電位差\(V_{AB}\ [V]\)は以下の様に表すことができます。
$$ V_{AB} = E \times d \ [V] $$
電位差\(V\ [V]\)と仕事\(W\ [J]\)の関係
\(+1\ [C]\)の点電荷を移動させるときの仕事の大きさが\(V\ [V]\)であるから、
$$ \begin{align} 仕事 &= 電荷1\ [C] \times 電位差V\ [V] \\ W &= Q \times V \end{align} $$
となります。











コメント