問題
図のように直列に接続された二つの平行平板コンデンサに \(120\) V の電圧が加わっている。コンデンサ \(\rm C_1\) の金属板間は真空であり、コンデンサ \(\rm C_2\) の金属板間には比誘電率 \(ε_r\) の誘電体が挿入されている。コンデンサ \(\rm C_1\) 、\(\rm C_2\) の金属板間の距離は等しく、 \(\rm C_1\) の金属板の面積は \(\rm C_2\) の 2 倍である。このとき、コンデンサ \(\rm C_1\) の両端の電圧が \(80\) V であった。次の(a)及び(b)の問に答えよ。
ただし、コンデンサの端効果は無視できるものとする。
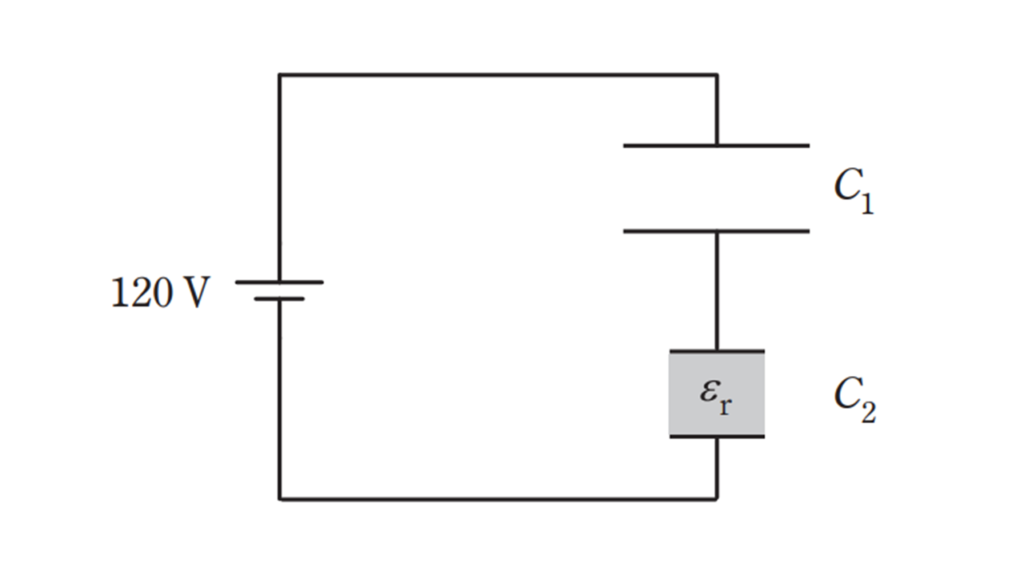
(a) コンデンサ\(\rm C_2\) の誘電体の比誘電率 \(ε_r\) の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \(1\) (2) \(2\) (3) \(3\) (4) \(4\) (5) \( 5\)
(b) \(C_1\) の静電容量が \(30\) μF のとき、 \(\rm C_1\) と \(\rm C_2\) の合成容量の値 [μF] として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \(10\) (2) \(20\) (3) \(30 \) (4) \(40\) (5) \(50\)
解説
答え:(a)-(4)、(b)-(2)
(a) 誘電体の比誘電率を求める
コンデンサ\(\rm C_1\)、\(\rm C_2\)の静電容量を求める
コンデンサ\(\rm C_1\)の極板の面積を\(S \rm[m^2]\)、真空中の誘電率を\(ε_0 \rm [F/m] \)、極板間の距離を\(d \rm [m]\)とすると、コンデンサ\(\rm C_1\)と\(\rm C_2\)の静電容量\(C_1\)と\(C_2\)はそれぞれ以下のように表すことができます。
\( C_1 = ε_0 \displaystyle \frac{S}{d} \)
\( \begin{align} C_2 &= ε_rε_0 \displaystyle \frac{ \displaystyle \frac{1}{2}S}{d} \\ \\ &= ε_r ε_0 \displaystyle \frac{S}{2d} \end{align} \)
よって、コンデンサ\(\rm C_2\)の静電容量は、コンデンサ\(\rm C_1\)の\( \displaystyle \frac{ε_r}{2}\)倍になります。
コンデンサ\(\rm C_1\)、\(\rm C_2\)に蓄えられる電荷の量を求める
問で与えられた図より、コンデンサ\(\rm C_1\)、\(\rm C_2\)は、直列に接続されているため、コンデンサ\(\rm C_1\)、\(\rm C_2\)に蓄えられる電荷の量は等しくなります。
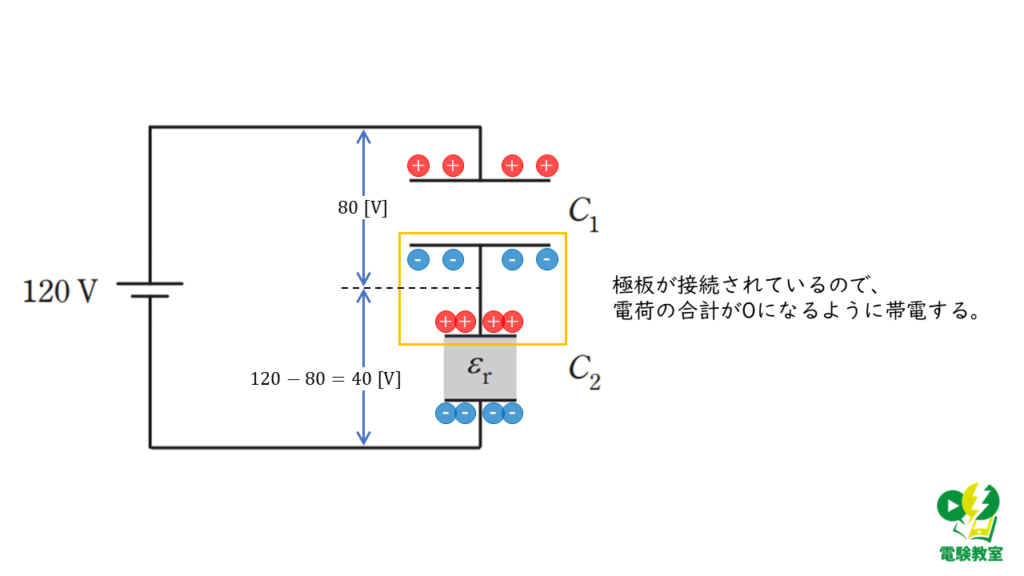
問題文より、コンデンサ\(\rm C_1\)に印加される電圧の大きさは\(80\)Vであるので、蓄えられる電荷の量\(Q_1\)[C]は、
\( \begin{align} Q_1 &= C_1 \times V_1 \\ \\ &= ε_0 \displaystyle \frac{S}{d} \times 80 \\ \\ &= ε_0 \displaystyle \frac{80S}{d} \end{align} \)
と表すことができます。一方、コンデンサ\(\rm C_2\)に蓄えられる電荷の量\(Q_2\)は、
\( \begin{align} Q_2 &= C_2 \times V_2 \\ \\ &= ε_r ε_0 \displaystyle \frac{S}{2d} \times \left( 120 – 80 \right) \\ \\ &= ε_r ε_0 \displaystyle \frac{40S}{2d} \end{align} \)
となります。
コンデンサが直列に接続されているため、 コンデンサ\(\rm C_1\)、\(\rm C_2\)に蓄えられる電荷の量は等しくなるので、
\( \begin{align} Q_1 &= Q_2 \\ \\ ε_0 \displaystyle \frac{80S}{d} &= ε_r ε_0 \displaystyle \frac{40S}{2d} \\ \\ 80 &= 40 \times \displaystyle \frac{ε_r}{2} \\ \\ ε_r &= 4 \end{align} \)
よって、答えは(4)になります。
(b) \(\rm C_1\) と \(\rm C_2\) の合成容量の値 [μF] を求める
コンデンサ\(\rm C_2\)の静電容量の大きさを求める
問題文より、コンデンサ\(\rm C_1\)の静電容量は、\(30\)[μF]でなので、(a)で求めた比誘電率\(ε_r = 4\)を用いて、
\( C_2 = C_1 \times \displaystyle \frac{ε_r}{2} = 30 \times \displaystyle \frac{4}{2} = 60 \)[μF]
と計算することができます。
したがって、\(\rm C_1\) と \(\rm C_2\) の合成容量\(\rm C\)の大きさは、
\( \begin{align} \displaystyle \frac{1}{C} &= \displaystyle \frac{1}{C_1} + \displaystyle \frac{1}{C_2} \\ \\ &= \displaystyle \frac{1}{30} + \displaystyle \frac{1}{60} \\ \\ &= \displaystyle \frac{2+1}{60} \\ \\ \displaystyle \frac{1}{C} &= \displaystyle \frac{3}{60} =\displaystyle \frac{1}{20} \end{align} \)
よって、合成容量の大きさは\(20\)[μF]となり、答えは(2)になります。











コメント