問題
図のように,真空中で2枚の電極を平行に向かい合せたコンデンサを考える。各電極の面積を\(A\ \rm [m^2]\),電極の間隔を\(l\) [m]とし,端効果は無視すると,静電容量は \( \fbox { (ア) } \) [F]である。このコンデンサに直流電圧源を接続し,電荷\(Q\) [C]を充電してから電圧源を外した。このとき,電極間の電界\( E \) = \( \fbox { (イ) } \) [V/m]によって静電エネルギー\(W \) = \( \fbox { (ウ) } \) [J]が蓄えられている。この状態で電極間隔を増大させると静電エネルギーも増大することから,二つの電極間には静電力の\( \fbox { (エ) } \)が働くことが分かる。
ただし,真空の誘電率を\(ε_0 \) [F/m]とする。
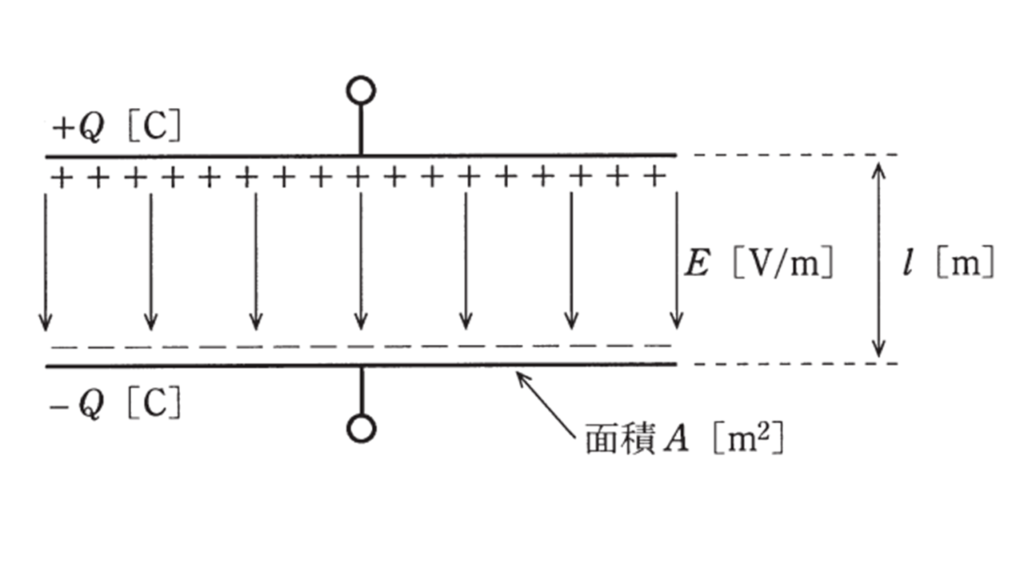
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
$$ \begin{array}{ccccc} \ &(ア)&(イ)&(ウ)&(エ)\\ \hline (1) &ε_0\displaystyle \frac{A}{l} &\displaystyle \frac{Ql}{ε_0 A} &\displaystyle \frac{Q^2 l}{ε_0A} &引力 \\ \hline (2) &ε_0\displaystyle \frac{A}{l} &\displaystyle \frac{Q}{ε_0 A} & \displaystyle \frac{Q^2 l}{2ε_0A} &引力 \\ \hline (3) & \displaystyle \frac{A}{ε_0 l} & \displaystyle \frac{Ql}{ε_0 A} & \displaystyle \frac{Q^2 l}{2ε_0A} & 斥力 \\ \hline (4) &ε_0\displaystyle \frac{A}{l} &\displaystyle \frac{Q}{ε_0 A} &\displaystyle \frac{Q^2 l}{ε_0A} &斥力 \\ \hline (5) &ε_0\displaystyle \frac{A}{l} &\displaystyle \frac{Q}{ε_0 A} & \displaystyle \frac{Q^2 l}{2ε_0A} &斥力 \\ \hline \end{array} $$
解説
答え:(2)
(ア):平行板コンデンサの静電容量について
各電極の面積を\(A\ \rm [m^2]\),電極の間隔を\(l\) [m],真空の誘電率を\(ε_0 \) [F/m]とすると,静電容量\(C\) [F]は以下の式で表すことができます。
\( C = ε_0 \displaystyle \frac{A}{l} \)
(イ):電荷\(Q\)で充電しているときの電極間の電界\( E \)について
電荷\(Q\) [C]で充電しているとき,極板間の電位差(電圧)\(V\)は,
\( V = \displaystyle \frac{Q}{C} = \displaystyle \frac{Ql}{ε_0 A}\)
と表すことができるので,電極間の電界\( E \) [V/m]の大きさは,
\( \begin{align} E &= \displaystyle \frac{V}{l} \\ \\ &= \displaystyle \frac{\displaystyle \frac{Ql}{ε_0 A}}{l} \\ \\ &= \displaystyle \frac{Q}{ε_0 A} \end{align} \)
となります。
(ウ):静電エネルギーの大きさについて
静電エネルギーの式は,
\( W = \displaystyle \frac{1}{2} QV\)
で表すことができます。よって、(ウ)は以下の式となります。
\( \begin{align} W &= \displaystyle \frac{1}{2}QV \\ \\ &= \displaystyle \frac{1}{2} \times Q \times \displaystyle \frac{Ql}{ε_0 A} \\ \\ &= \displaystyle \frac{Q^2l}{2ε_0 A} \end{align} \)
(エ):静電気力の種類
上側の極板はプラスに帯電し,下側の極板はマイナスに帯電しているので,2つの極板の間には引き合う力(引力)が働きます。
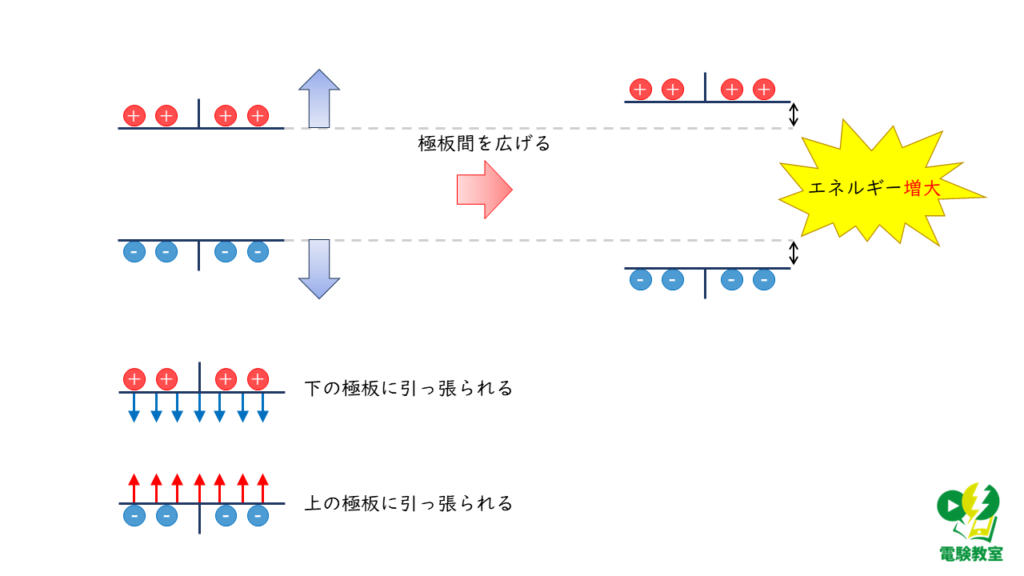
物体に加える力\(F\)[N],物体の移動距離\(l\) [m]とエネルギー\(W\) [J]の間には,
\( W = F \times \delta l \)
の関係式が成り立ちます。力とエネルギーの式より、
「極板間にはたらいている力に逆らって力を加える=エネルギーを与える」となるため,
問題文中の「極板間距離を広げると,エネルギーは増大した」の記述より,極板間には引力が働いていたと考えられます。











コメント