問題
図1の端子a−d間の合成静電容量について,次の(a)及び(b)の問に答えよ。
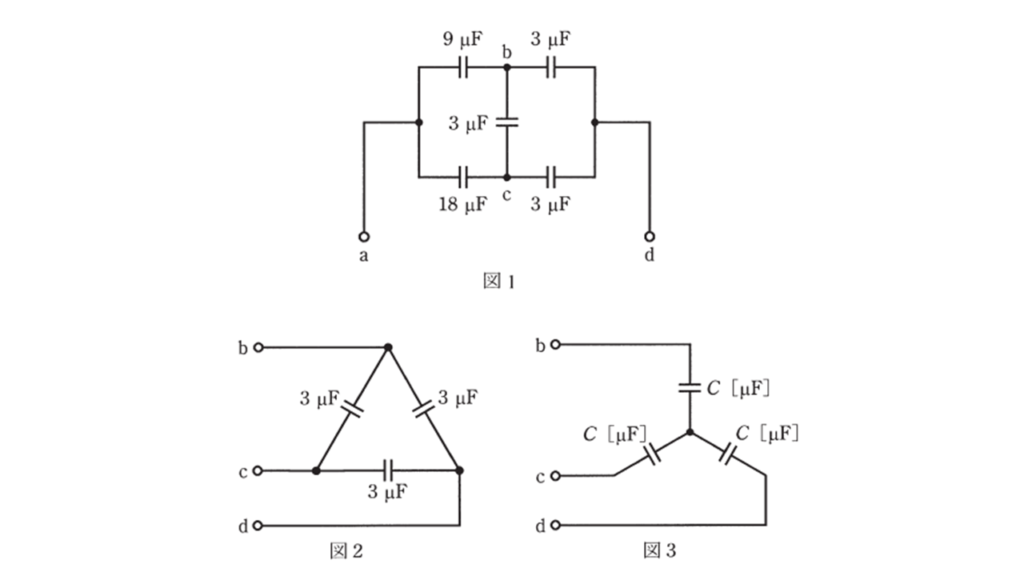
(a) 端子b−c−d間は図2のようにΔ結線で接続されている。これを図3のようにY結線に変換したとき,電気的に等価となるコンデンサ\(C\)の値[μF]として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \(1.0\) (2) \(2.0\) (3) \(4.5\) (4) \(6.0\) (5) \(9.0\)
(b) 図3を用いて,図1の端子b−c−d間をY結線回路に変換したとき,図1の端子a−d間の合成静電容量\(C_0\)の値[μF]として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \(3.0\) (2) \(4.5\) (3) \(4.8\) (4) \(6.0\) (5) \(9.0\)
解説
答え:(a)-(5),(b)-(3)
(a) \(\Delta\)-Y変換したときの静電容量\(C\)を求める
容量リアクタンス\(X_C\) [\(\Omega\)]の形で表す
静電容量[F]の形のままでは,\(\Delta\)-Y変換の式が適用しにくいため,まず静電容量[F]から容量リアクタンス\(X_C\) [\(\Omega\)]に変換します。
角周波数を\(\omega\)とすると,\(\Delta\)結線時の容量リアクタンス\(X_Cd\)とY結線時容量リアクタンス\(X_Cy\)はそれぞれ以下のように表すことができます。
\( X_{Cd} = \displaystyle \frac{1}{3\omega} \) [\(\Omega\)]
\( X_{Cy} = \displaystyle \frac{1}{\omega C} \) [\(\Omega\)]
\(\Delta\)-Y変換により静電容量を求める
3つの抵抗値[Ω]の値が等しい場合,\(\Delta\)-Y変換による抵抗値[Ω]の大きさは,以下の図のようになります。
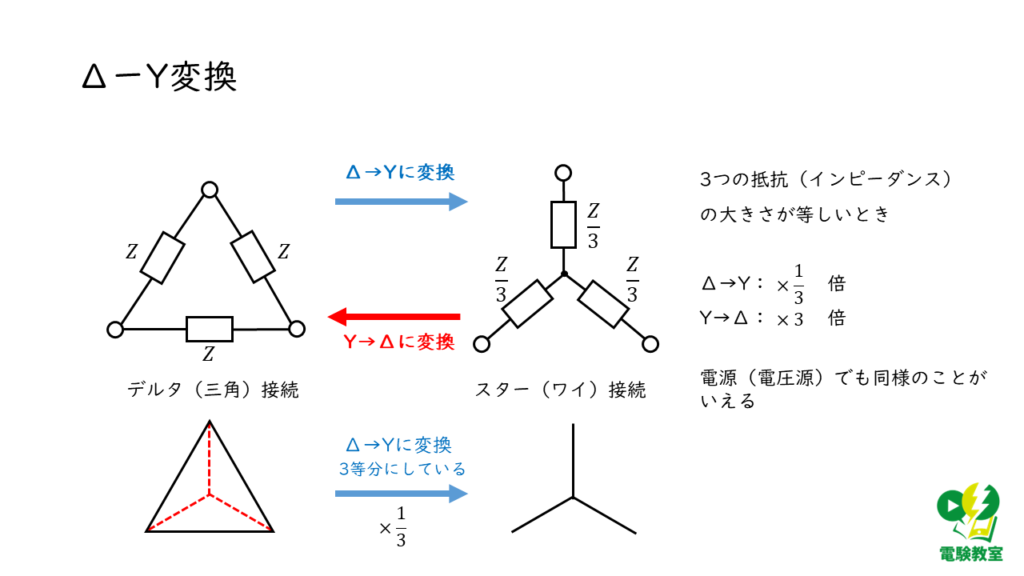
したがって,容量リアクタンス\( X_{Cd}\)と\( X_{Cy}\)は以下のような関係にあります。
\(\begin{align} X_{Cy} &= \displaystyle \frac{1}{3} \times X_{Cd} \\ \\ \displaystyle \frac{1}{\omega C} &= \displaystyle \frac{1}{3} \times \displaystyle \frac{1}{3\omega} \\ \\ \displaystyle \frac{1}{\omega C} &= \displaystyle \frac{1}{9\omega} \end{align}\)
分母を比べると
\( C = 9\)
であることが分かります。よって,答えは(5)となります。
端子b,c間に注目すると,\(\Delta\)結線の回路とY結線の回路は以下のように考えることができます。
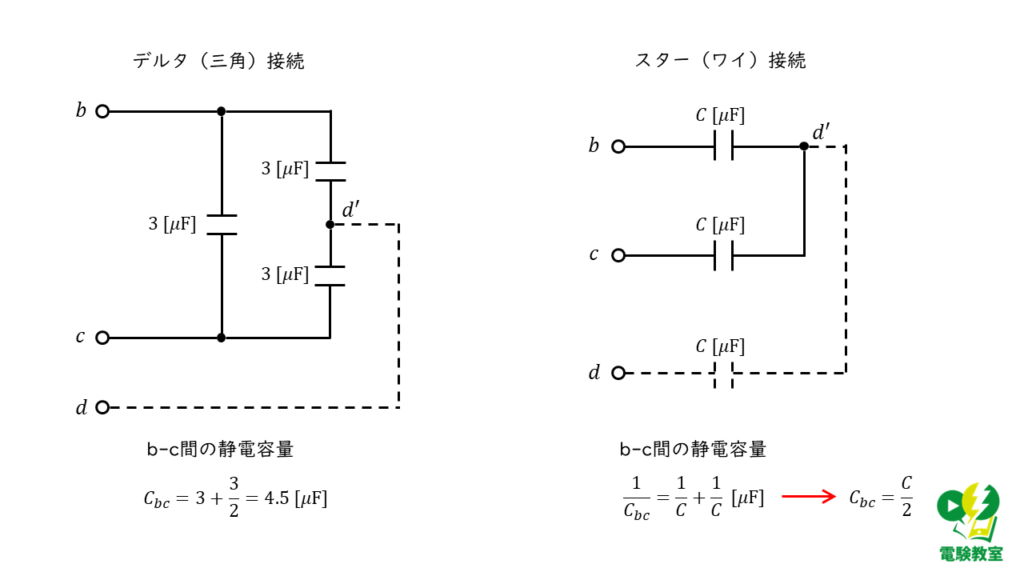
回路を等価変化しているだけなので,端子b,c間の静電容量の大きさは変化しません。
よって,Y変換時の静電容量\(C\)の大きさは,
\(\begin{align} \displaystyle \frac{1}{4.5} &= \displaystyle \frac{2}{C} \\ \\ \displaystyle \frac{2}{9} &= \displaystyle \frac{2}{C} \end{align}\)
となり,静電容量\(C=9\) [μF]と求めることができます。
(b) 図1の端子a−d間の合成静電容量\(C_0\)の値を求める
(a)で求めたY変換時の回路を図1に当てはめると,以下の図4のように回路を書き表す頃ができます。
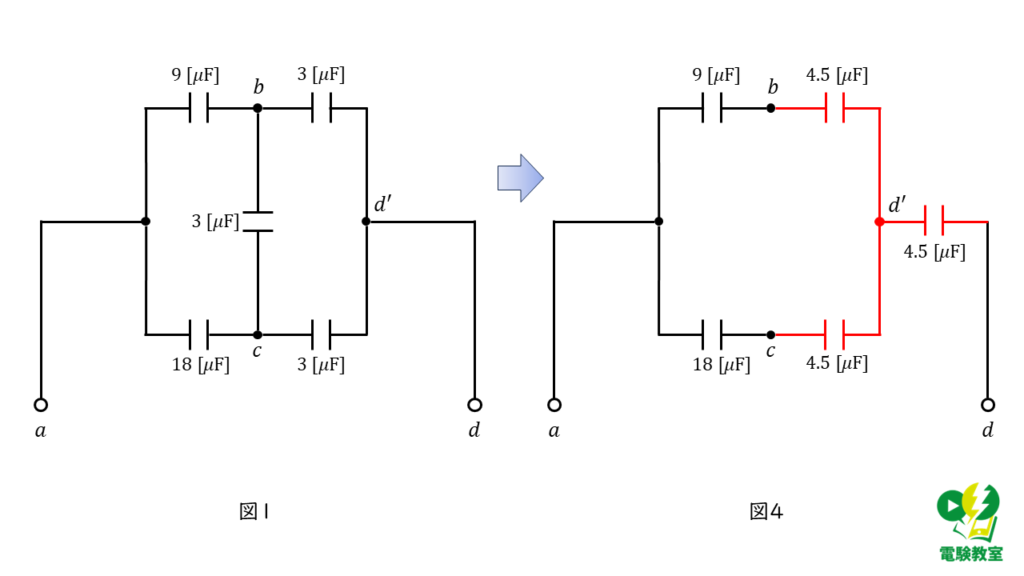
並列接続部分の静電容量を求める
図4より並列回路部分の合成容量\(C’\)は、
\( \begin{align} C’ &= \displaystyle \frac{1}{\left( \displaystyle \frac{1}{9} + \displaystyle \frac{1}{9} \right)} + \displaystyle \frac{1}{\left(\displaystyle \frac{1}{18}+\displaystyle \frac{1}{9}\right)} \\ \\ \\ &= \displaystyle \frac{1}{\displaystyle \frac{2}{9}} + \displaystyle \frac{1}{\displaystyle \frac{3}{18}} \\ \\ &= \displaystyle \frac{9}{2} + \displaystyle \frac{18}{3} \\ \\ &=4.5 +6 =10.5 \end{align} \)
回路全体の静電容量を求める
回路全体の静電容量\(C_0\) [μF]は、
\(\begin{align} \displaystyle \frac{1}{C_0} &= \displaystyle \frac{1}{10.5} + \displaystyle \frac{1}{9} \\ \\ \displaystyle \frac{1}{C_0} &= \displaystyle \frac{9+10.5}{10.5 \times 9} \\ \\ C_0 &= \displaystyle \frac{10.5 \times 9}{9+10.5} \approx 4.83 \end{align} \)
よって、(b)の答えは、(3)となります。











コメント