問題
図のように,真空中において二つの小さな物体A,Bが距離\(r\) [m]を隔てて鉛直線上に置かれている。Aは固定されており,Aの真下にBがある。物体A,Bはそれぞれ,質量\(m_A\) [kg],\(m_B\) [kg]をもち,電荷\(+q_A\) [C],\(−q_B\) [C]を帯びている。\(q_A>0,q_B>0\)とし,真空の誘電率を\(ε_0\) [F/m]とする。次の(a)及び(b)の問に答えよ。
ただし,小問(a)においては重力加速度g [m/s2]の重力を,小問(b)においては無重力を,それぞれ仮定する。物体A,Bの間の万有引力は無視する。
(a) 重力加速度\(g \ \rm [m/s^2]\)の重力のもとでBを初速度零で放ったとき,BはAに近づくように上昇を始めた。このときの条件を表す式として,正しいものを次の(1)~(5)のうちから一つ選べ。
(1) \(\displaystyle \frac{q_A q_B}{4πε_0 r^2} > m_Bg \) (2) \(\displaystyle \frac{q_A q_B}{4πε_0 r}>m_Bg\) (3) \(\displaystyle \frac{q_A q_B}{4πr}>m_Bg\)
(4) \(\displaystyle \frac{q_A q_B}{2πε_0 r^2}>m_Bg\) (5) \(\displaystyle \frac{q_A q_B}{2πε_0r}>m_B g\)
(b) 無重力のもとでBを下向きの初速度\(v_B\) [m/s]で放ったとき,Bは下降を始めたが,途中で速度の向きが変わり上昇に転じた。このときの条件を示す式として,正しいものを次の(1)~(5)のうちから一つ選べ。
(1) \(\displaystyle \frac{1}{2}m_B v^2_B<\displaystyle \frac{q_A q_B}{4πε_0r^2}\) (2) \(\displaystyle \frac{1}{2}m_B v^2_B < \displaystyle \frac{q_A q_B}{4πε_0 r}\) (3) \(m_B v_B < \displaystyle \frac{q_A q_B}{4πε_0r^2}\)
(4) \(m_B v_B < \displaystyle \frac{q_A q_B}{4πε_0 r}\) (5) \(\displaystyle \frac{1}{2}m_B v_B<\displaystyle \frac{q_A q_B}{4πε_0r^2}\)
解説
答え:(a)-(1),(b)-(2)
(a) 物体Bが物体Aに近づく動きをする条件を求める
物体Bにはたらく力を求める
物体Bにはたらく静電気力の大きさは,クーロンの法則を用いて以下のように表すことができます。
\( F_e = \displaystyle \frac{q_A q_B}{4πε_0 r^2} \) [N]
一方,物体Bにはたらく重力は,質量\(m_B\) [kg]と重力加速度\(g\) [\( \rm m/s^2\)]を用いて,
\( F_g = m_B g \) [N]
となります。物体Bにはたらく2つの力を問題の図に書き加えると下図2のように表されます。
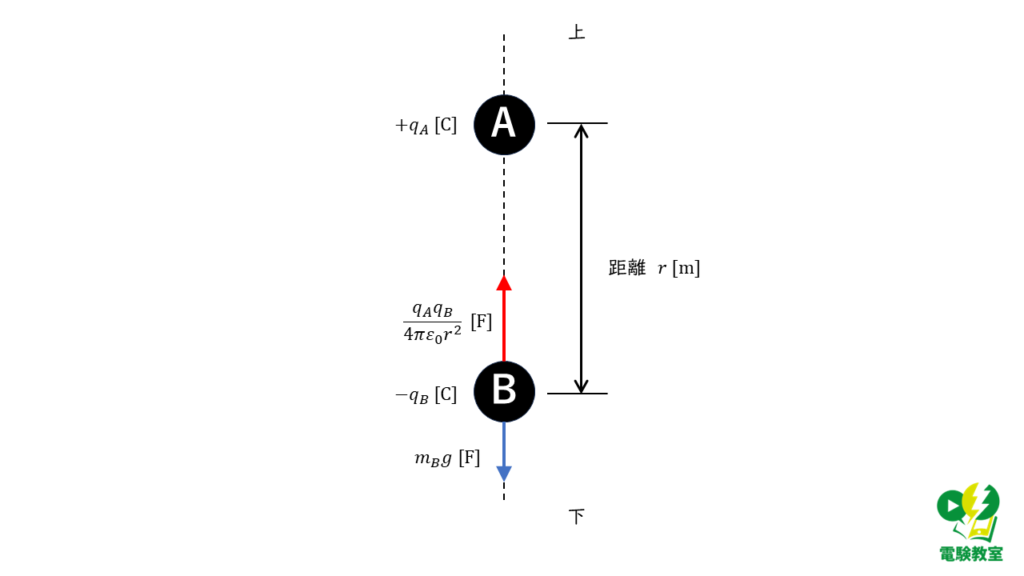
問題の条件から2力の大小を決める
問題文には,「…Bを初速度零で放ったとき,BはAに近づくように上昇を始めた。」と記載があるので,物体Aの方向に向かい力の方が大きいことが読み取れます。
図2より,物体Aに近づく方向の力は静電気力であることから,(a)の答えは,
\( \displaystyle \frac{1}{2}m_B v^2_B<\displaystyle \frac{q_A q_B}{4πε_0r^2}\)
となります。
(b) 運動している物体Bが物体Aに近づく動きをする条件を求める
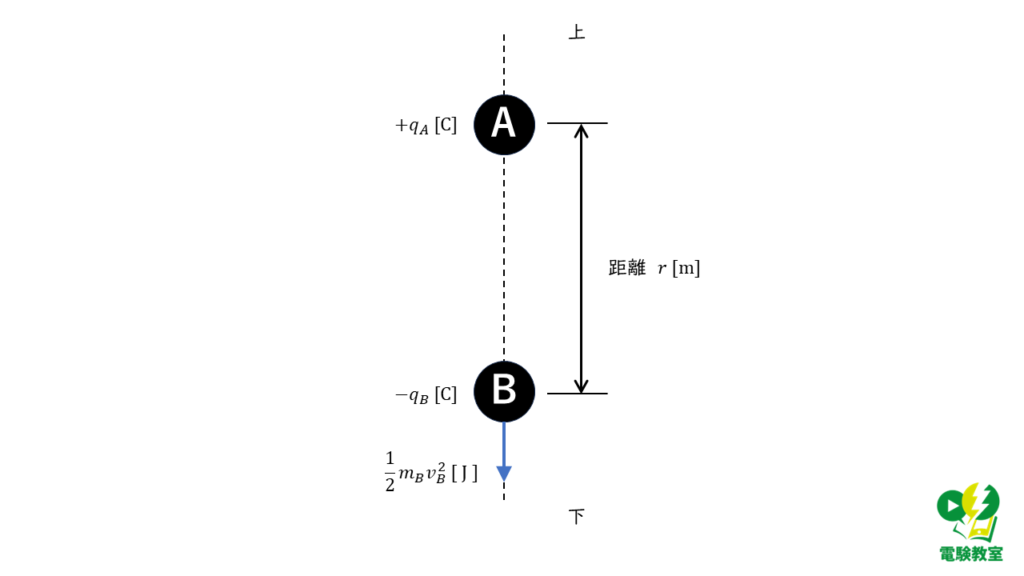
物体Bの運動エネルギーを求める
問題文には,「無重力のもとBを下向きの初速度\(v_B\) [m/s]で放った」と記載がるので,物体Bの持つ運動エネルギーの大きさは,
\( \displaystyle \frac{1}{2} m_B v_B^2 \)
と表すことができます。
物体Bが初めの状態で持っている電気的なエネルギーを求める
電荷を帯びた物体が持つ電気的なエネルギー\(W\) [J]の大きさは,電位\(V\)[V]と電荷\(Q\) [C]を用いて,
\( W = V \times Q\)
と表すことができます。
物体Bが置かれている地点は,物体Aが持つ電荷による電位\(V_A\)の位置となるので,
\( V = V_A = \displaystyle \frac{q_A}{4πε_0 r}\) [V]
となります。物体Bは電荷\(q_B\) [C]を持っているので,電気的なエネルギー\(W\)の大きさは,
\(\begin{align} W &= V_A \times q_B \\ \\ &= \displaystyle \frac{q_A}{4πε_0 r} \times q_B \\ \\ &= \displaystyle \frac{q_A q_B}{4πε_0 r} \end{align} \)

問題の条件から2力の大小を決める
問題文には,「…Bは下降を始めたが,途中で速度の向きが変わり上昇に転じた。」と記載があるので,運動エネルギーよりも電気的なエネルギーの方が大きいと読み取れます。
したがって,問題文の動きと合致する条件は,
\(\displaystyle \frac{1}{2}m_B v^2_B < \displaystyle \frac{q_A q_B}{4πε_0 r}\)
となります。











コメント